Навигация
ФАЛ, принимающие одинаковые значения на всех наборах аргументов, называются равными
1. ФАЛ, принимающие одинаковые значения на всех наборах аргументов, называются равными.
2. ФАЛ существенно зависит от аргумента Хi, если
F(X1,X2,...,Хi-1,0,Xi+1,...,Xn) ![]()
F(X1,X2,...,Хi-1,1,Xi+1,...,Xn)
В противном случае она зависит не существенно, а соответствующий аргумент наз. фиктивным.
Например:
| Х1 | Х2 | Х3 | F(X1,X2,Х3) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Видно, что Х3 – фиктивный аргумент. Это показывает, что в функцию можно ввести любое число фиктивных аргументов, от которых она существенно не зависит. Этот прием в дальнейшем потребуется для выполнения ряда преобразований.
Все ФАЛ от 2-х аргументов. Сведем их в единую таблицу 2.1.
| Таблица 2.1. | ||||||
| № функции | Значение функции на наборах логических переменных | Наименование функции | Обозначение функции | |||
| X1 | 0 | 0 | 1 | 1 | ||
| X2 | 0 | 1 | 0 | 1 | ||
| f0(X1,X2) | 0 | 0 | 0 | 0 | Константа "ноль" | f(X1,X2)=0 |
| f1(X1,X2) | 0 | 0 | 0 | 1 | Конъюнкция, произведение | f(X1,X2)= X1& X2 f(X1,X2)= X1 f(X1,X2)= X1 · X2 f(X1,X2)= X1 X2 |
| f2(X1,X2) | 0 | 0 | 1 | 0 | Запрет по X2 | X1 Δ X2 |
| f3(X1,X2) | 0 | 0 | 1 | 1 | Переменная X1 | f(X1,X2)= X1 |
| f4(X1,X2) | 0 | 1 | 0 | 0 | Запрет по X1 | X2 Δ X1 |
| f5(X1,X2) | 0 | 1 | 0 | 1 | Переменная X2 | f(X1,X2)= X2 |
| f6(X1,X2) | 0 | 1 | 1 | 0 | Сложение по mod2 (неравнозначность) | f(X1,X2)= X1 |
| f7(X1,X2) | 0 | 1 | 1 | 1 | Дизъюнкция | f(X1,X2)= X1 f(X1, X2)= X1+ X2 |
| f8(X1,X2) | 1 | 0 | 0 | 0 | Стрелка Пирса | f(X1, X2)= X1 |
| f9(X1,X2) | 1 | 0 | 0 | 1 | Равнозначность | f(X1, X2)= X1 f(X1, X2)= X1~X2 |
| f10(X1,X2) | 1 | 0 | 1 | 0 | Инверсия X2 | f(X1, X2)=^X2 f(X1, X2)=X2 |
| f11(X1,X2) | 1 | 0 | 1 | 1 | Импликация от X2 к X1 | f(X1, X2)= X2 |
| f12(X1,X2) | 1 | 1 | 0 | 0 | Инверсия X1 | f(X1, X2)=^X1 f(X1, X2) = X1 |
| f13(X1,X2) | 1 | 1 | 0 | 1 | Импликация от X1 к X2 | f(X1, X2)= X1 |
| f14(X1,X2) | 1 | 1 | 1 | 0 | Штрих Шеффера | f(X1, X2)= X1|X2 |
| f15(X1,X2) | 1 | 1 | 1 | 1 | Константа "единица" | f(X1, X2)=1 |
Эти функции введены формально. Однако им можно придавать определенный "логический" смысл. Алгебра логики часто называется исчислением высказываний.
При этом под высказываниями понимается всякое предложение, относительно которого можно утверждать, что оно истинно или ложно.
Например:
В=<один плюс один - два>
есть истинное высказывание.
Рассмотрим, какое смысловое содержание можно вложить в некоторые сложные высказывания на примере ФАЛ 2-х аргументов.
ИнверсияЧитается НЕ Х или Х с чертой, отрицание Х.
Возьмем, например, такое высказывание: А=<Киев-столица Франции>, тогда сложное высказывание НЕ А означает: не верно, что А, т.е. не верно, что <Киев-столица Франции>.
Из простых высказываний можно строить более сложные, применяя так называемые связи.
Логические связи – это ФАЛ, аргументами которых являются простые высказывания.
КонъюнкцияВозьмем 2 высказывания:
А=<Москва – столица РФ>
В=<дважды два - четыре>
тогда сложное высказывание: А & В будет истинным, так как истинны оба этих высказывания.
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если истинному высказыванию приписать значение '1', а ложному - '0', то сложное высказывание можно назвать произведением.
| X1 | X2 | f1(X1,X2) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.
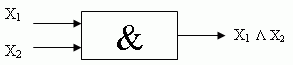
Это сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.
| X1 | X2 | f1(X1,X2) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Читается X1 ИЛИ X2: Некоторое отличие от смысла союза "или", принятого в русском языке: в данном случае этот союз употребляется в смысле объединения, а не разъединения.

Это сложное высказывание истинно тогда, когда истинны или ложны одновременно оба высказывания.
Отсюда следует, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания.
Например,
А=<дважды два - пять>
B=<один плюс два - шесть>
А~В равнозначны. Импликация
Это сложное высказывание ложно только тогда, когда X1 – истинно, а X2 – ложно.
| X1 | X2 | f1(X1,X2) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Читается: если X1, то X2. При этом X1 – посылка, X2 – следствие.
Если посмотреть на таблицу истинности, то может показаться странным название этой функции, т.к. из него следует, что истинным может быть высказывание, составленное из двух ложных.
Но в действительности, все верно, т.к. содержанием высказываний в алгебре логики не интересуются.
Тогда из ложной посылки может следовать ложное следствие и это можно считать верным: <если Киев – столица Франции>, то <2-квадрат 3>.
ЭквивалентностиВ некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.
Дизъюнкция:
х ![]() х
х ![]() х
х ![]() х
х ![]() ...
... ![]() х
х ![]() х
х ![]() х= х,
х= х,
т.е. истинность высказывания не изменится, если его заменить более коротким, таким образом, это правило приведения подобных членов:
![]()
![]()
– постоянно истинное высказывание.
0 ![]() x = x
x = x
x1![]() x2 = x2
x2 = x2![]() x1
x1
- (переместительный) коммуникативный закон.
x1![]() х2
х2![]() х3 = (x1
х3 = (x1![]() х2)
х2) ![]() х3 = x1
х3 = x1![]() (х2
(х2![]() х3)
х3)
- сочетательный закон.
Конъюнкция:
х ![]() х
х ![]() х
х ![]() х...
х... ![]() х
х ![]() х
х ![]() х= х
х= х
правило приведения подобных членов:
![]()
![]() - постоянно ложное высказывание
- постоянно ложное высказывание
![]() - постоянно ложное высказывание
- постоянно ложное высказывание
![]()
![]()
1![]()
![]()
при нечетном числе членов, 0 - при четном числе членов
Правило де Моргана![]()
![]()
Докажем для двух переменных с помощью таблицы истинности:
| Х1 | Х2 |
|
|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Операция поглощения:
Х ![]() XY = X
XY = X
или в общем виде
X ![]() X*f(X,Y,Z...) = X;
X*f(X,Y,Z...) = X;
Операция полного склеивания:
![]() (по Y)
(по Y)
![]() (по Х)
(по Х)
Операция неполного склеивания:
![]()
Похожие работы
... схемами с односторонней проводимостью, имеющими конечное число входов и один выход. Простейшие электронные схемы, реализующие элементарные булевы функции (НЕ, И, ИЛИ, ИЛИ-НЕ, И-НЕ), называются логическими элементами (ЛЭ). Аналитическая форма представления булевых функций При решении конкретных технических задач булевы функции, отражающие логические связи, наиболее часто задаются в табличной ...
... значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот. Диаграмма для двух логических переменных (для ДСНФ): Для трех переменных: Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие на границе карты. При числе переменных 5 и ...
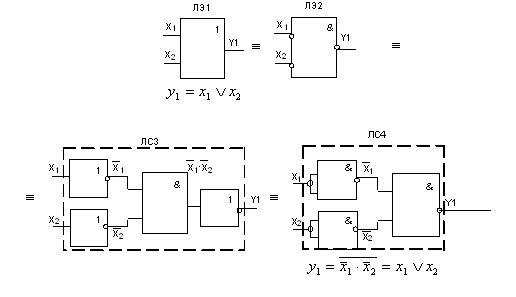
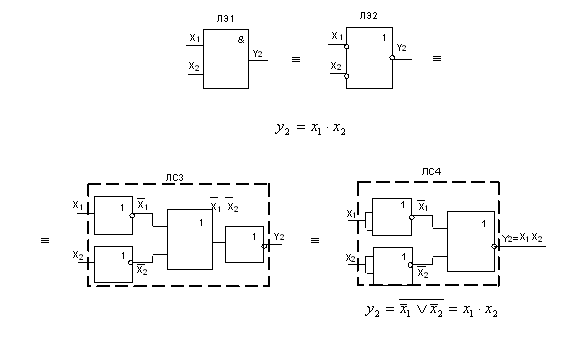
... дизъюнкции заменить на операцию конъюнкции (либо наоборот) и проинвертировать все переменные, то результат окажется инверсным прежнему значению. Используя принцип двойственности алгебры логики, реализуем логическое выражение (7) в различных базисах. Рис. 2 Из рис.2 следует: если переименовать все входы и выходы логического элемента ЛЭ1 на инверсные значения и заменить ЛЭ дизъюнкции на ЛЭ2 ...
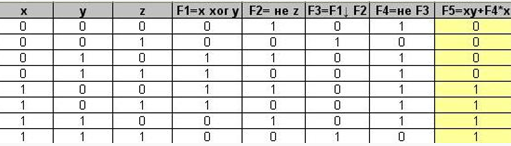
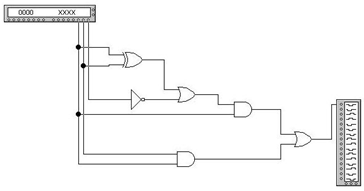
... Поглощение 17 F17=X1+X1’*X2=X1+X2 Поглощение 18 F18=(X1*X2)’=X1’+X2’ 1 правило де Моргана 19 F19=(X1+X2)’=X1’*X2’ 2 правило де Моргана Задание 3 Спроектировать цифровую схему, выполняющая указанные действия и состоящую из простейших элементов И, ИЛИ, НЕ. Результаты подтвердить построением таблицы истинности и соответствующими временными диаграммами. Спроектировать цифровую схему ...


0 комментариев