Навигация
Особенности цифровой фототриангуляции
1.4 Особенности цифровой фототриангуляции
Пирамиды изображений для хранения цифровых изображений.
При обработке цифровых изображений[7] при ПФТ часто возникает необходимость просмотра снимков в уменьшенном масштабе. Для этих целей в программах ПФТ посчитанные один раз изображения уменьшенного масштаба, записываются и хранятся на диске во время всего сеанса обработки в виде «пирамид изображений». В этом случае информационное поле описывается упорядоченным набором изображений, располагаемых одно над другим.
Для формирования пирамиды изображений исходный цифровой снимок разбивается на блоки (обычно 2 х 2 пикселя). Для каждого блока вычисляется среднее арифметическое значение яркости, которое и будет присвоено пикселю для данного блока на следующем уровне пирамиды. Эта процедура повторяется необходимое число раз. Каждое последующее изображение пирамиды будет иметь разрешение в 2 раза меньше предыдущего, а занимаемый объём памяти соответственно в 4 раза
Хранение пирамид изображений оправдано, так как увеличевает скорость обработки.
Тайловая структура организации данных цифровых изображений.
В качестве модели организации данных цифровых изображений[7] используется тайловая структура, которая заключается в следующем:
Исходное изображение делится на блоки (тайлы), размер которых фиксирован.
При необходимости обработки конкретного участка изображения осуществляется перемещение на данный адрес и считывается нужный файл. Эта организация данных позволяет быстро считывать с диска и отображать на экране отдельные участки изображения.
Реляционная модель организации данных.
Для обеспечения гибкости сбора данных и хранения результатов измерения координат точек снимков в современных программных продуктах используется реляционная модель данных[7].
| Таблица 1 «Сведения о точках сети» | Таблица 2 «Сведения о снимках» | |
| Номер точки | Идентификатор снимка | |
|
|
| |
| Описание точки | Другие параметры |
| Таблица 3 «Сведения о точках снимка» |
| Номер точки |
| Идентификатор снимка |
| Измеренные х,у |
| Другие параметры |
Таблица 1 служит для хранения номеров и координат опорных, контрольных и связующих точек (номера точек не должны повторяться).
Таблица 2 служит для хранения информации о снимках, используемых в обработке. В качестве данных выступают идентификатор снимка, элементы внешнего ориентирования, результаты внутреннего ориентирования снимка и т.п.
В таблице 3 хранятся непосредственно измеренные координаты точек снимков х,у. Каждому измерению х,у в этой таблице соответствует номер измеряемой точки и идентификатор снимка, на котором производилось измерение.
Такая организация данных позволяет однозначно сопоставить каждому измерению соответствующую точку местности (сети) и снимок, на котором выполнено измерение. Она позволяет хранить «бесконечное» число опорных, контрольных, связующих точек и результатов измерения их координат.
Алгоритмы автоматического отождествления соответственных точек снимков.
Ключевым алгоритмом автоматизации фотограмметрических измерений является поиск соответственных точек на паре снимков[7].
В соответствии с методами представления видеоинформации все множество алгоритмов отождествления можно разделить на три класса:
- алгоритмы площадного сопоставления (ABM), основанные на сравнении двумерных функций изображений;
- алгоритмы, базирующиеся на сопоставлении структурных описаний (FBM);
- алгоритмы, в основе которых лежит разложение функции изображения по некоторому базису.
Рассмотрим подробнее первую группу. Здесь в качестве примитивов (элементов описаний), участвующих при сопоставлении двух изображений служат пиксели. Точность этих алгоритмов составляет от 0,1 до 0,2 размера пикселя. Они чувствительны к изменению радиометрических и геометрических свойств изображения, требуют больших вычислительных затрат и характеризуются большой вероятностью грубой ошибки в областях расположения высотных объектов и плохих или повторяющихся структур. Примерами площадных алгоритмов являются алгоритм взаимной корреляции и метод наименьших квадратов. Критерием подобия для этих алгоритмов соответственно служат коэффициент взаимной корреляции и сумма квадратов разностей значений яркостей сопряженных участков изображений.
Mетод взаимной корреляции.
Суть метода заключается в вычислении функции взаимной корреляции, которую для дискретных функций можно записать в виде:
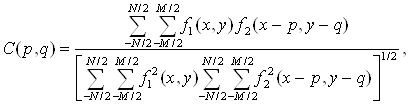 (1.23)
(1.23)
где p и q – продольный и поперечный параллаксы на изображении f2(x, y).
M и N – соответственно ширина и высота образца или пределы, в которых определена функция f1(x,y).
Функция взаимной корреляции обладает следующими свойствами:
1) ![]()
2) если f1(x,y) и f2(x-p,y-q) независимы, то C(p, q)=0;
3) C(p,q)=1 тогда и только тогда, когда существует такое число b¹0, что ![]() .
.
Фактически алгоритм отыскания соответствия между функциями f1(x,y) и f2(x-p, y-q) сводится к нахождению таких p0 и q0, при которых функция C(p, q) максимальна.
Преимущество этого метода простота реализации.
К недостаткам алгоритма взаимной корреляции относятся:
- большой объем вычислений;
- алгоритм устойчиво работает только при следующих условиях: снимаемая местность плоская, взаимные углы наклона и разворота снимков не превышают 20-30°, а разномасштабность снимков менее 20-30%.
Метод наименьших квадратовДля метода наименьших квадратов в качестве критерия подобия служит функция суммы квадратов разностей между яркостями пикселей двух изображений.
Пусть на ограниченном участке (x'[-M/2, M/2], y'[-N/2, N/2]) между функциями f1 и f2 существует зависимость:
![]() (1.24)
(1.24)
Для определения искомых величин p0 и q0 составим функцию:
![]() (1.25)
(1.25)
Данную функцию решаем под условием минимума:
![]() , (1.26)
, (1.26)
Если известны приближенные значения неизвестных параметров (![]() ), то раскладывая функцию(1.25) в ряд Тейлора и ограничиваясь величинами первого порядка малости получаем линейное уравнение относительно неизвестных Dp0 и Dq0:
), то раскладывая функцию(1.25) в ряд Тейлора и ограничиваясь величинами первого порядка малости получаем линейное уравнение относительно неизвестных Dp0 и Dq0:
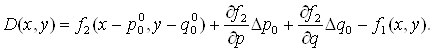 (1.27)
(1.27)
В результате приходим к системе уравнений поправок:
![]() (1.28)
(1.28)
где A – матрица коэффициентов уравнений поправок;
dX – вектор-столбец поправок к приближенным значениям неизвестных (Dp0 и Dq0);
V – вектор невязок уравнений, который характеризует величины шумовых составляющих.
От системы уравнений поправок переходим к системе нормальных уравнений:
![]() (1.29)
(1.29)
где ![]() и
и ![]() .
.
После определения Dp0 и Dq0 уточняют значения искомых параметров p0 и q0 и затем выполняют следующую итерацию. Этот процесс повторяется до получения требуемой точности вычисления неизвестных.
Алгоритм наименьших квадратов по сравнению с методом взаимной корреляции обладает рядом следующих преимуществ.
Во-первых, метод наименьших квадратов позволяет оценить точность определения искомых параметров. Для оценки точности используют среднюю квадратическую ошибку (СКО) единицы веса, которая будет характеризовать влияние шумовых составляющих и качество образца, и СКО определения параметров p0 и q0, характеризующие точность отождествления соответственно по осям x и y. Значение СКО единицы веса определяется по известной формуле:
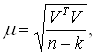 (1.30)
(1.30)
где n – количество уравнений поправок, а k – количество неизвестных.
СКО определения неизвестных p0 и q0 выражаются формулами:
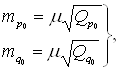 (1.31)
(1.31)
где ![]() и
и ![]() – соответствующие диагональные элементы обратной матрицы нормальных уравнений.
– соответствующие диагональные элементы обратной матрицы нормальных уравнений.
Во-вторых, метод наименьших квадратов позволяет вести не глобальный поиск соответственной точки, подставляя все возможные значения p и q, как в методе взаимной корреляции, а вдоль направления градиента функции.
В-третьих, как показывает практика, из всех разработанных алгоритмов отождествления метод наименьших квадратов дает наилучшие результаты в отношении точности.
В-четвертых, геометрические ограничения, накладываемые на положение и ориентацию снимков относительно плоскости объектов, несколько ослаблены при использовании метода наименьших квадратов по сравнению с методом взаимной корреляции.
К недостаткам метода наименьших квадратов следует отнести:
- алгоритм, как и все методы площадного отождествления, устойчиво работает только при незначительной разномасштабности и взаимных углах наклона и разворота снимков;
- для получения корректного решения требуется достаточно точно задать параметры p0 и q0.
Широкое распространение на практике получили следующие программные продукты цифровой фототриангуляции:
1) Softplotter фирмы Vision;
2) DPW фирмы Leica;
3) Imagine Station фирмы Intergraph;
4) Match AT – первая программа полностью автоматической ПФТ;
5) Helava Automated Triangulation System;
6) Phodis AT.
Среди российских ЦФС, в которых реализована программа цифровой ПФТ, распространение получили:
1) ЦФС Photomod фирмы Ракурс;
2) Talka, разработанная институтом проблем управления РАН;
3) ЦНИИГАиК.
Они имеют различные алгоритмы и способы реализации, высокую скорость обработки данных, удобный пользовательский интерфейс, гибкость и универсальность, возможность интерактивного режима работы оператора на всех этапах технологических процессов построения сети. По уровню автоматизации все программы ЦФТ делятся на: автоматические и полуавтоматические.
Основными технологическими процессами, которые существуют в любой программе цифровой фототриангуляции [7] являются:
1) создание проекта;
2) внутреннее ориентирование снимков;
3) измерение координат точек снимков;
4) предварительное построение сети;
5) уравнивание сети;
6) оценка точности построения сети.
 X,Y,Z
X,Y,Z  Элементы внешнего ориентирования снимка
Элементы внешнего ориентирования снимка
0 комментариев