Навигация
Современные методы анализа себестоимости
1.3 Современные методы анализа себестоимости
Анализ себестоимости продукции, работ и услуг имеет очень важное значение. Он позволяет выяснить тенденции изменения данного показателя, выполнения плана по его уровню, определить влияние факторов на его прирост, установить резервы и выработать корректирующие меры по использованию возможностей снижения себестоимости продукции.
Объектами анализа себестоимости продукции являются следующие показатели:
• полная себестоимость товарной продукции в целом и по элементам затрат;
• затраты на рубль продукции;
• себестоимость отдельных изделий;
• отдельные статьи затрат;
• затраты по центрам ответственности.
Для эффективного управления процессом формирования себестоимости продукции очень важно правильно определить сумму постоянных и переменных затрат. Для этой цели используются разные методы: алгебраический, графический, статистический, основанный на корреляционно-регрессионном анализе, селективный, построенный на содержательном анализе каждой статьи и элемента затрат.
Алгебраический метод можно применять при наличии информации о двух точках объема продукции в натуральном выражении (х1 и х2) и соответствующих им затратам (z1 и z2). Переменные затраты на единицу продукции (b) определяют следующим образом:
b = (z1 – z2) / (х1 – х2) (1.1)
Узнав переменные затраты на единицу продукции, нетрудно подсчитать сумму постоянных затрат (а):
а = z2 – bх2 или а = z1 – bх1 (1.2)
Графический метод нахождения суммы постоянных затрат состоит в следующем. На графике откладываются две точки, соответствующие общим издержкам для минимального и максимального объема производства (рис. 1.2). Затем они соединяются до пересечения с осью ординат, на которой откладываются уровни издержек. Точка, где прямая пересекает ось ординат, показывает величину постоянных затрат, которая будет одинаковой как для максимального, так и минимального объема производства.
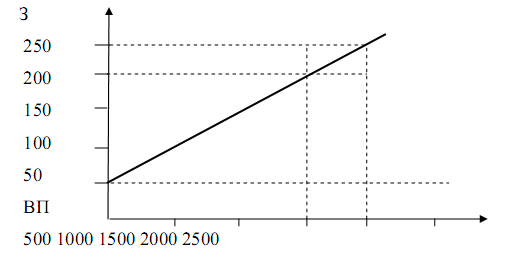
Рис. 1.2. Графический метод нахождения суммы постоянных затрат. Источник: [22, с. 348]
Сумму постоянных затрат в уравнении связи (Y = a + bx) можно определить и с помощью корреляционного анализа, если имеется достаточно большая выборка данных о затратах и выпуске продукции. В качестве примера представим табл. 1.1
Таблица 1.1 Данные о затратах (Y) и объемах производства продукции (x)
| Месяц | х | у | ху | х² |
| Январь | 120 | 62 | 7440 | 10400 |
| Февраль | 130 | 63 | 8190 | 16900 |
| Март | 150 | 65 | 9750 | 22500 |
| Апрель | 140 | 64 | 8960 | 19600 |
| Май | 180 | 68 | 12240 | 32400 |
| Июнь | 200 | 70 | 14000 | 40000 |
| Июль | 200 | 70 | 14000 | 40000 |
| Август | 270 | 77 | 20790 | 72900 |
| Сентябрь | 280 | 78 | 21840 | 78400 |
| Октябрь | 250 | 75 | 18750 | 62500 |
| Ноябрь | 200 | 71 | 14200 | 40000 |
| Декабрь | 180 | 67 | 12060 | 32400 |
| Итого: | 2300 | 830 | 162220 | 472000 |
Составим систему уравнений и решим ее:
![]() na + b∑x = ∑y,
na + b∑x = ∑y,
![]() a∑x + b∑x² = ∑xy.
a∑x + b∑x² = ∑xy.
12а + 2300b = 830,
2300а + 472000b = 162220.
Умножив все члены первого уравнения на 2300, а второго на 12, получим следующую систему уравнений:
![]() 27600а + 5290000b = 1909000,
27600а + 5290000b = 1909000,
27600а + 5664000b = 1946640,
374000b = 37640;
b = 0,1,
а = (830 – 2300 · 0,1) / 12 = 50.
Уравнение связи Y = 50 + 0,1x показывает, что сумма постоянных затрат в данном примере составляет 50 тыс. руб., а переменные затраты на единицу продукции – 100 руб.
Если вместо количества произведенной продукции возьмем ее стоимость, то коэффициент b в уравнении регрессии покажет удельные переменные затраты, а коэффициент а – сумму постоянных затрат.
Селективный метод позволяет более точно определить сумму постоянных и переменных затрат, но он более трудоемкий по сравнению с рассмотренными выше. Однако в условиях современных технологий обработки экономической информации этот процесс упрощается, если предусмотреть деление затрат на постоянные и переменные в компьютерных программах и в первичных документах.
Описанные выше методы являются наиболее распространенными и в силу своей простоты наиболее часто используемыми на предприятиях в настоящее время.
0 комментариев