МНОЖЕННЯ ЧИСЕЛ, ЩО ПРЕДСТАВЛЕНІ В ФОРМІ З ФІКСОВАНОЮ КОМОЮ
Метод скороченого множення
Дії, що виконуються під час множення обернених кодів, залежать від знаку множника
МЕТОДИ ПРИСКОРЕННЯ ОПЕРАЦІЇ МНОЖЕННЯ
Апаратні методи прискорення операції множення в двійковій системі числення
Метод множення з запам’ятовуванням проміжних перенесень
МЕТОДИ ДІЛЕННЯ ЧИСЕЛ В ЦОМ
Ділення чисел, що представлені в доповняльному коді
Навигация
Дії, що виконуються під час множення обернених кодів, залежать від знаку множника
Виконання операцій множення і ділення у двійковій системі числення
52201
знак
8
таблиц
30
изображений
1. Дії, що виконуються під час множення обернених кодів, залежать від знаку множника.
2. Добуток обернених кодів співмножників дорівнює оберненому коду результату тільки у випадку додатного множника.
3. Якщо множник є від'ємним числом, то обернений код добутку одержується додаванням поправок 
і 
до добутку обернених кодів співмножників.
Оскільки поправки мають різну вагу, то послідовність їх додавання залежить від того, з яких розрядів множника починається множення (табл. 3.7).
Приклад 3.7. Помножити обернені коди чисел А = - 0, 10100 і В = 0, 10011, використовуючи метод 1.
Розв'язання. Для даних чисел маємо: [А]моб=11,01011; [В]об= 0,10011. Оскільки B>0, то поправки не додаються. Послідовність дій, що виконуються в процесі множення, подані у вигляді табл. 3.8.
Відповідь: [С]моб =11,1010000011; С= - 0, 0101111100.
Таблиця 3.7 - Послідовність додавання поправок для оберненого коду
| Методи множення | Е т а п и | ||
| З молодших розрядів множника | Додавання
| Множення за методом і додатковий зсув на один розряд після його завершення | Додавання
|
| Зі старших розрядів множника | Додавання
| Додатковий зсув на один розряд і після нього множення за методом | Додавання
|
Таблиця 3.8 - Перший приклад множення обернених кодів
Приклад 3.8. Помножити обернені коди чисел А = - 0,10100 і В = - 0, 10011, використовуючи метод 2.
Розв'язання. Для даних чисел маємо: [А]моб=11,01011; [В]об= 1,01100. Оскільки B<0, то додаються поправки. Послідовність дій, що виконуються в процесі множення, подані у вигляді табл. 3.9.
Таблиця 3.9 - Другий приклад множення обернених кодів
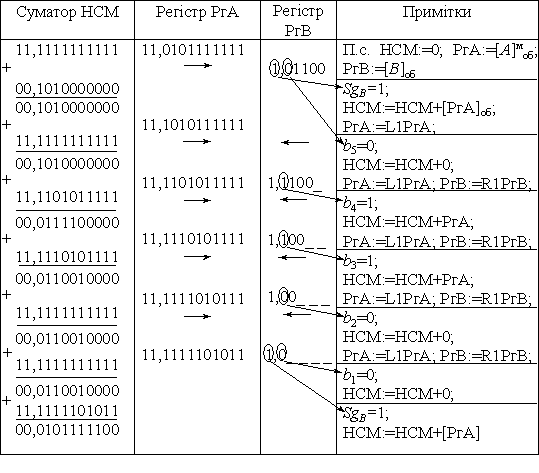
Відповідь: С= 0, 0101111100.
3.2.4. Множення доповняльних кодів чисел
У випадках, коли числа в машині зберігаються в доповняльних кодах, доцільно всі операції над числами робити на суматорі доповняльного коду. Однак при цьому під час множення виникає ряд особливостей, які необхідно враховувати. Тому розглянемо правила множення операндів, що представлені в доповняльному коді.
Нехай множене А - будь-яке число, а множникB > 0, тобто А = [A]д і [В]д
. Тоді
.
Згідно з теоремою про додавання доповняльних кодів можна стверджувати, що права частина цього співвідношення відповідає доповняльному коду результату. Таким чином, у випадку додатного множника добуток доповняльних кодів співмножників дорівнює доповняльному коду результату.
Розглянемо випадок, коли множене А - будь-яке число, а множник B < 0, тобто А=[A]д і [В]д
. Виходячи з означення доповняльного коду 
. Отже,
.
Тоді
.
Звідси випливає, що коли множник є від'ємним числом, то доповняльний код добутку одержується додаванням поправки 
до добутку доповняльних кодів співмножників.
Таким чином, у загальному випадку, в процесі множення доповняльних кодів операндів одержуємо одночасно знакову і цифрову частини добутку.
Правила множення з додаванням поправки наведені в табл. 3.10.
Приклад 3.9. Помножити доповняльні коди чисел А = - 0, 10100 і В = 0, 10011, використовуючи метод 1.
Розв'язання. Для даних чисел маємо: [А]мд =11,01100; [В]д= 0,10011. Оскільки B>0, то поправка не додається. Послідовність дій, що виконуються в процесі множення, подані у вигляді табл. 3.11.
Відповідь: [С]мд =11,1010000100; С= - 0, 0101111100.
Таблиця 3.10 - Правила множення з додаванням поправки
| Методи множення | Етапи | |
| З молодших розрядів множника | Множення за методом і додатковий зсув на один розряд після його завершення | Додавання
|
| Зі старших розрядів множника | Додавання
| Додатковий зсув на один розряд і після нього множення за методом |
Таблиця 3.11 - Перший приклад множення доповняльних кодів
Приклад 3.10. Помножити доповняльні коди чисел А = - 0,10100 і В = - 0, 10011, використовуючи метод 2.
Розв'язання. Для даних чисел маємо: [А]мд=11,01011; [В]д= 1,01100. Оскільки B<0, то додається поправка. Послідовність дій, що виконуються в процесі множення, подані у вигляді табл. 3.12.
Таблиця 3.12 - Другий приклад множення доповняльних кодів
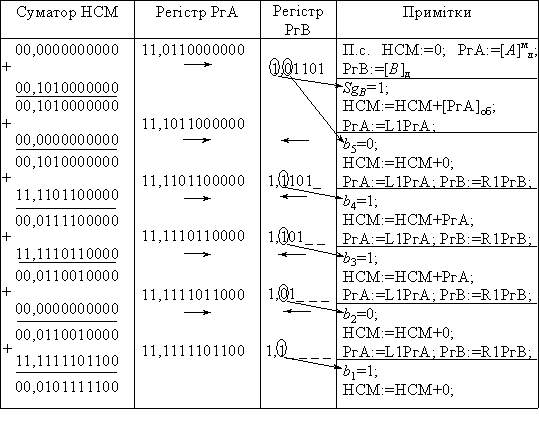
Відповідь: С= 0, 0101111100.
Похожие работы
... автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми. 1.5 Контроль виконання арифметичних операцій Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або ...
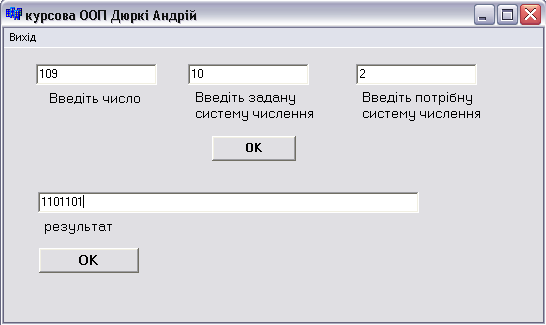
... в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). 6. Програмна реалізація Програма розроблена для перетворення чисел з однієї системи числення в іншу.Реалізована в середовищі програмування Borland C++Builder. Лістінг програми: #include <vcl.h> #pragma hdrstop #include "Unit1.h" #include <math.h> #include < ...
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... тову складність операцій у полі, то можна оцінити результуючу бітову складність операцій з многочленами. Щоб відрізняти арифметичну складність від бітової в оцінках ми використовуватимемо символи і . Обчислення значень многочленів. Нехай – довільне кільце. Розглянемо добре відомий алгоритм Руфіні - Горнера для обчислення значень многочлена над кільцем у точці. Останнє число ,і буде шуканим ...
0 комментариев