МНОЖЕННЯ ЧИСЕЛ, ЩО ПРЕДСТАВЛЕНІ В ФОРМІ З ФІКСОВАНОЮ КОМОЮ
Метод скороченого множення
Дії, що виконуються під час множення обернених кодів, залежать від знаку множника
МЕТОДИ ПРИСКОРЕННЯ ОПЕРАЦІЇ МНОЖЕННЯ
Апаратні методи прискорення операції множення в двійковій системі числення
Метод множення з запам’ятовуванням проміжних перенесень
МЕТОДИ ДІЛЕННЯ ЧИСЕЛ В ЦОМ
Ділення чисел, що представлені в доповняльному коді
Навигация
Ділення чисел, що представлені в доповняльному коді
Виконання операцій множення і ділення у двійковій системі числення
52201
знак
8
таблиц
30
изображений
3.5.3. Ділення чисел, що представлені в доповняльному коді
Коли в пам'яті машини числа зберігаються в доповняльному коді, то виникає задача пошуку найраціональніших методів ділення в доповняльному коді. Так само як і в разі множення, тут можливі два варіанти:
- переведення операндів у прямий код, одержання частки звичайним способом і переведення його в доповняльний код перед записом у пам'ять;
- ділення операндів у доповняльному коді з одержанням частки в необхідному вигляді.
Реалізація другого варіанта так само проста, як і першого. Необхідно тільки керувати логікою утворення цифр частки. Принципово є можливість одержувати ці цифри як з виходу БІЦ, так і минаючи цей блок. При цьому буде формуватись обернений код частки, який неважко перетворити в доповняльний код. Практична реалізація такого ділення може бути організована двома шляхами:
- аналізуючи знаки операндів блок керування БК організує передавання знакових цифр остач із НСМ в регістр частки так, щоб результат завжди формувався в оберненому коді (тобто додатна частка складалась із прямих значень цифр, а від'ємне - з обернених);
- аналізуючи знаки операндів блок БК організує спочатку або віднімання модуля дільника від модуля діленого, або віднімання модуля діленого від модуля дільника, для того щоб логіка утворення частки в разі всіх можливих комбінацій знаків операндів залишалась незмінною. Разом з тим частка має обов'язково формуватись в оберненому коді.
Розглянемо чотири можливих випадки, що обумовлені комбінаціями знаків доповняльних кодів операндів.
Випадок 1. А > 0; B > 0; C = A/B > 0.
Ділення виконується як звичайно: знак частки визначається шляхом додавання знакових цифр операндів за модулем 2 і одночасно формується доповнення модуля дільника до двох. Цифри частки одержуються шляхом інвертування знакових цифр остач в БІЦ.
Випадок 2. А > 0; B < 0; C = A/B < 0.
Ділення починається з віднімання модуля дільника від діленого. У разі відсутності переповнення розрядної сітки знак першої остачі обов'язково буде дорівнювати 1. Отже, його потрібно без інвертування надіслати до знакового розряду РгС. Продовжується ділення звичайним шляхом, але знакові цифри остач надходять до регістра частки минаючи БІЦ. По закінченню ділення в РгС утворюється обернений код від'ємної частки. Додаванням одиниці до (п + 1)-го розряду частки здійснюється одночасно округлення частки і переведення оберненого коду в доповняльний.
Приклад 3.18. Поділити число А = 0,1010 на число В = - 0,1101, використовуючи ділення в доповняльному коді.
Розв'язання. Для даних чисел маємо: [А]д = 0,1010; [В]д = 1,0011.
Усі дії, що виконуються в процесі ділення, наведені в табл. 3.20. Обернений код частки має вигляд 1,00111. Додавши одиницю до наймолодшого розряду і відкидаючи його, одержимо [С]д = 1,0100
Відповідь: С= - 0,1100.
Таблиця 3.20 - Приклад ділення в доповняльному коді для випадку А > 0 і B < 0
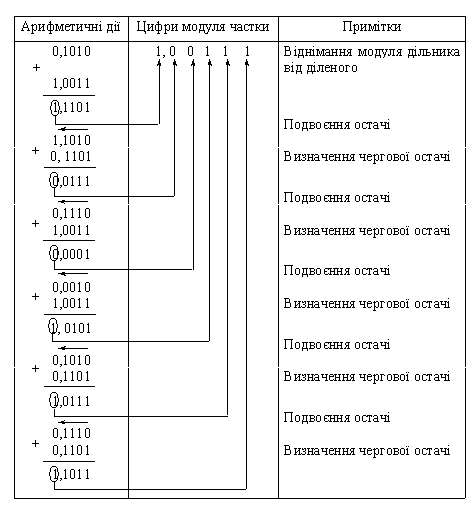
Випадок 3. А < 0; B > 0; C = A/B < 0.
Цей випадок є дзеркальним відображенням попереднього. Отже, для того щоб одержати обернений код від'ємної частки, необхідно надсилати знакові цифри остач до регістра частки через БІЦ. Наприкінці ділення, так саме як у другому випадку, необхідно додати одиницю до (п + 1)-го розряду частки для переведення його в доповняльний код і округлення одночасно.
Приклад 3.19. Поділити число А = - 0,1010 на число В = 0,1101, використовуючи ділення в доповняльному коді.
Розв'язання. Для даних чисел маємо: [А]д = 1,0110; [В]д = 0,1101.
Усі дії, що виконуються в процесі ділення, наведені в табл. 3.21. Обернений код частки має вигляд 1,00111. Додавши одиницю до наймолодшого розряду і відкидаючи його, одержимо [С]д = 1,0100
Відповідь: С= - 0,1100.
Таблиця 3.21 - Приклад ділення в доповняльному коді для випадку А < 0 і B > 0
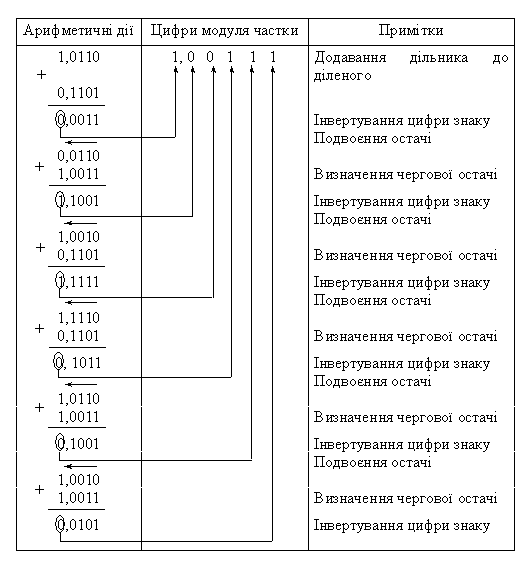
Випадок 4. А < 0; B < 0; C = A/B > 0.
Ділення починається з віднімання модуля діленого від модуля дільника. Для цього достатньо перетворити попередньо тільки код дільника. В процесі ділення знакові цифри остач необхідно надсилати до регістра частки без інвертування, минаючи БІЦ, оскільки частка має бути додатною, а її доповняльний код - співпадати з прямим.
3.5.4. Особливості ділення чисел з плаваючою комою
Для чисел 
і 
, що представлені в формі з плаваючою комою, частка визначається за формулою:
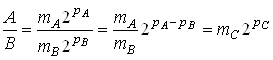
де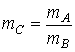 
, 
.
Звідси випливає, що процес ділення складається з чотирьох етапів:
- ділення мантис;
- віднімання порядків;
- нормалізація мантиси частки;
- корегування порядку частки.
Перші два етапи можуть виконуватись одночасно, оскільки вони незалежні один від одного. При цьому ділення мантис повністю співпадає з діленням чисел, що представлені в формі з фіксованою комою. Відміна полягає лише в тому, що мантиси операндів можуть співвідноситись одна з одною довільно. Оскільки мантиси діленого і дільника - нормалізовані числа, то можливі такі випадки: 
; 
.
Коли мантиса діленого більше або дорівнює мантисі дільника, то на початку ділення одержується цифра частки, що дорівнює 1 і яка записується в цілу частину частки. Решта дій над мантисами аналогічні діям над числами, що представлені в формі з фіксованою комою. Одержана при цьому мантиса частки буде мати порушення нормалізації праворуч. Воно усувається шляхом зсуву коду мантиси на один розряд управо і, відповідно, корегується порядок частки шляхом додавання одиниці до різниці порядків.
Коли мантиса діленого менше мантиси дільника, то на початку ділення одержується цифра частки, що дорівнює 0 і яка записується в цілу частину частки. Далі ділення мантис продовжується за правилами ділення чисел, що представлені в формі з фіксованою комою. Одержана при цьому мантиса частки буде мати нормалізовану форму.
Під час виконання операції ділення чисел з плаваючою комою можуть мати місце такі особливі випадки.
Якщо дільник дорівнює нулю, то формується сигнал "Зупинка машини".
Оскільки в процесі ділення порядки віднімаються, то можливе переповнення розрядної сітки порядків. Коли виникає переповнення в бік від'ємних значень порядку і воно не усувається після нормалізації і корегування порядку, то мантисі результату приписується машинний нуль, а порядку - найбільше від'ємне число.
У разі переповнення додатного порядку необхідно формувати ознаку переповнення порядку.
Ці особливі випадки можна передбачити в алгоритмі операції ділення введенням аналізатора дільника на нуль і корегування частки на підставі ознак результату.
Похожие работы
... автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми. 1.5 Контроль виконання арифметичних операцій Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або ...
... в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). 6. Програмна реалізація Програма розроблена для перетворення чисел з однієї системи числення в іншу.Реалізована в середовищі програмування Borland C++Builder. Лістінг програми: #include <vcl.h> #pragma hdrstop #include "Unit1.h" #include <math.h> #include < ...
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... тову складність операцій у полі, то можна оцінити результуючу бітову складність операцій з многочленами. Щоб відрізняти арифметичну складність від бітової в оцінках ми використовуватимемо символи і . Обчислення значень многочленів. Нехай – довільне кільце. Розглянемо добре відомий алгоритм Руфіні - Горнера для обчислення значень многочлена над кільцем у точці. Останнє число ,і буде шуканим ...
0 комментариев