МНОЖЕННЯ ЧИСЕЛ, ЩО ПРЕДСТАВЛЕНІ В ФОРМІ З ФІКСОВАНОЮ КОМОЮ
Метод скороченого множення
Дії, що виконуються під час множення обернених кодів, залежать від знаку множника
МЕТОДИ ПРИСКОРЕННЯ ОПЕРАЦІЇ МНОЖЕННЯ
Апаратні методи прискорення операції множення в двійковій системі числення
Метод множення з запам’ятовуванням проміжних перенесень
МЕТОДИ ДІЛЕННЯ ЧИСЕЛ В ЦОМ
Ділення чисел, що представлені в доповняльному коді
Навигация
МЕТОДИ ПРИСКОРЕННЯ ОПЕРАЦІЇ МНОЖЕННЯ
Виконання операцій множення і ділення у двійковій системі числення
52201
знак
8
таблиц
30
изображений
3.3. МЕТОДИ ПРИСКОРЕННЯ ОПЕРАЦІЇ МНОЖЕННЯ
3.3.1. Основні поняття
Прискорення операції множення дозволяє істотно підвищити продуктивність ЦОМ, оскільки приблизно 70% свого часу вони витрачають на виконання цієї операції. Аналізуючи (3.2) - (3.5), можна намітити такі шляхи скорочення часу множення: зменшення часу додавання і зсуву кодів; зменшення кількості додавань і кількості зсувів кодів.
Оскільки прості методи множення передбачають виконання в кожному циклі зсув кодів тільки на один розряд, то зменшити час зсуву неможливо тому, що кола для зсуву реалізують, як правило, з найменшою затримкою сигналів.
Зменшення часу додавання двох кодів досягається за рахунок ускладнення кіл формування розрядних сум і перенесень у суматорі. Але це ні яким чином не впливає на організацію процесу множення. Тому основні підходи щодо прискорення операції множення базуються на зменшенні кількості додавань і кількості зсувів кодів.
Відомі на цей час методи прискорення множення розподілені на дві великі групи: логічні й апаратні.
Логічними методами прискорення множення називають такі методи, реалізація яких не вимагає змін основної структури арифметичних кіл пристрою для множення (див. рис. 3.1 - 3.5), а прискорення досягається тільки за рахунок ускладнення схеми керування цим пристроєм. Стосовно пристроїв для множення паралельних кодів ознакою того, що ми маємо справу з логічним методом прискорення множення, є незалежність кількості додаткової апаратури (у порівнянні з вихідною схемою) від кількості розрядів співмножників.
Апаратні методи, прискорення множення вимагають для свого здійснення введення додаткової апаратури в основні арифметичні кола пристрою для множення.
Розрізняють апаратні методи першого порядку і другого порядку. Для апаратних методів першого порядку характерна лінійна залежність кількості додаткової апаратури від кількості розрядів у співмножниках п. Тоді як реалізація методів другого порядку вимагає введення додаткової апаратури, кількість якої пропорційна 
.
3.3.2. Логічні методи прискорення операції множення в двійковій системі числення
До логічних методiв прискорення операції множення належать: метод множення з пропусканням додавань у тих випадках, коли чергова цифра множнику є нуль; метод множення з перетворенням цифр множнику шляхом групування розрядiв i метод множення з послідовним перетворенням цифр множника.
В основi двох останніх логічних методiв лежить перехід до надлишкової двійкової системи числення з алфавітом {1, 0, 
}, який дозволяє зменшити кількість одиниць у коді множника, але при цьому в процесi множення будуть виконуватись операції додавання та віднімання.
Метод множення з пропусканням додавань є найпростішим з логічних методів прискорення множення. Схему керування взагалі простіше побудувати так, щоб за тактом зсуву щораз приділявся час на додавання, але додавання виконувалося б у залежності від цифри множника. Невелике ускладнення схеми керування, що дозволяє відводити час на додавання тільки тоді, коли воно дійсно необхідно, скорочує число тактів додавання в середньому вдвічі. Час множення за таким методом прискорення дорівнює:
.
Цей метод прискорення рівною мірою підходить для тих випадків, коли множення починається зі старших розрядів множника, і для випадків, коли множення починається з молодших розрядів.
Приклад 3.11. Помножити числа А = - 0, 10100 і В = 0, 10011, використовуючи метод множення з пропусканням додавань.
Розв'язання. Для даних чисел маємо: 
=1; 
= 0, 10100; 
=0; 
= 0, 10011. Визначаємо знак добутку: 
=1
0=1.
Усі дії, що виконуються в кожному циклі множення, наведені табл. 3.13.
Відповідь: С= - 0, 0101111100.
Таблиця 3.13 - Приклад множення за прискореним методом
Розглянемо тепер метод множення з перетворенням цифр множнику шляхом групування розрядiв.
Кількість циклів, що необхідні для реалізації операції множення, можна скоротити, якщо в кожному циклі аналізувати не один, а два або більше розрядів множнику, виконуючи після аналізу додавання або віднімання та зсув множнику на відповідну кількість розрядів (два або більше). Для організації прискореного множення множник розбивають на групи з двох розрядів і перетворюють його таким чином, щоб кожна група містила не більш одної значущої одиниці (додатної або від'ємної).
Правила перетворення множника з молодших розрядiв у разі групування по два розряди формулюються, враховуючи таке.
Комбінації 00, 01, 10 не перетворюються, а комбінація 11 замінюється комбінацією 1.0, яка містить від'ємну одиницю в даній групі розрядів і додатну одиницю, що передається до наступної групи розрядів множника.
З урахуванням одиниці, що передається з попередньої групи розрядів, у даній групі розрядів після перетворення може зустрітися одна з таких комбінацій:
00 - якщо дана група розрядів містить цифри 00 і з попередньої групи одиниця не передається або якщо дана група розрядів містить цифри 11 і одиниця передається з попередньої групи розрядів;
01 - якщо дана група містить цифри 01 і з попередньої групи одиниця не передається, або якщо дана група розрядів містить 00 і передається одиниця з попередньої групи розрядів;
10 - якщо дана група містить 10 і нема одиниці з попередньої групи або якщо дана група містить 01 і є одиниця з попередньої групи розрядів;
0 - якщо дана група розрядів містить 11 і нема одиниці з попередньої групи або якщо дана група містить 10 і є одиниця з попередньої групи.
Із сказаного випливають правила перетворенням множнику, починаючи з молодших груп розрядів, що наведені в табл. 3.14. Тут 
- цифри даної групи розрядів; 
- цифра, що передається з попередньої групи; 
- перетворені цифри даної групи; 
- цифра, що передається в наступну групу.
Таблиця 3.14 - Правила перетворенням множнику, починаючи з молодших груп розрядів
|
|
|
|
|
|
|
|
|
| 0 0 | 0 | 0 0 | 0 | 0 0 | 1 | 0 1 | 0 |
| 0 1 | 0 | 0 1 | 0 | 0 1 | 1 | 1 0 | 0 |
| 1 0 | 0 | 1 0 | 0 | 1 0 | 1 | 0 | 1 |
| 1 1 | 0 | 0 | 1 | 1 1 | 1 | 0 0 | 1 |
Застосовуючи ці правила необхідно враховувати, що старша значуща цифра перетвореного множника може знаходитися в розряді цілих, де неперетворений множник містить завжди нуль.
Приклад 3.12. Використовуючи групування розрядів, виконати перетворення множнику 001011111001100111, починаючи з молодших розрядів.
Розв'язання. Діючи за правилами, що наведені в табл. 3.14, одержимо
| 0 0 | 1 0 | 1 1 | 1 1 | 1 0 | 0 1 | 1 0 | 0 1 | 1 1 |
| +1 | +1 | +1 | +0 | +0 | +0 | +0 | +1 | |
| 0 1 | 0 | 0 0 | 0 | 1 0 | 0 1 | 1 0 | 1 0 | 0 |
Замість 11 одиниць у вихідному представленні множника одержуємо 8 додатних і від'ємних одиниць у перетвореному.
Відповідь: 010
000100110100.
Коли одразу аналізуються два розряди перетвореного множнику, то в процесі множення виконуються такі дії.
Якщо група містить комбінацію 00, то це означає, що протягом двох найближчих циклів множення не потрібно буде виконувати ні додавань, ні віднімань; при наявності комбінації 01 потрібно буде виконати одне додавання в першому з двох найближчих циклів множення, а у разі комбінації 10 - у другому. Коли група містить комбінацію 0, то буде потрібно виконати одне віднімання в першому з двох найближчих циклів множення.
У разі одночасного аналізу двох розрядів, починаючи зі старших, у правилах перетворення груп розрядів (табл. 3.15) враховується значення сусіднього розряду, що розташований праворуч від групи, яка аналізується. При цьому аналіз розрядів множника завжди починається з пустої групи, що дописується ліворуч від найстаршого розряду.
Приклад 3.13. Використовуючи групування розрядів, виконати перетворення множнику 001011111001100111, починаючи зі старших розрядів.
Розв'язання. Діючи за правилами, що наведені в табл. 3.15, одержимо
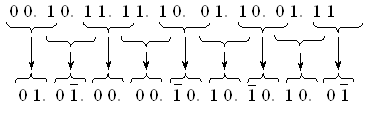
Замість 11 одиниць у вихідному представленні множника одержуємо 7 додатних і від'ємних одиниць у перетвореному.
Відповідь: 01000000100100.
Той чи інший метод перетворення тим ефективніше, чим менше в перетвореному множнику середня кількість додатних і від'ємних одиниць, тобто чим менше в середньому потрібно додавань і віднімань. Важлива також максимальна кількість додавань і віднімань, що можуть виконуватись під час множення.
Таблиця 3.15 - Правила перетворення множнику, починаючи зі старших груп розрядів
|
|
|
|
|
|
|
| 0 0 | 0 | 0 0 | 0 0 | 1 | 0 1 |
| 0 1 | 0 | 0 1 | 0 1 | 1 | 1 0 |
| 1 0 | 0 |
| 1 0 | 1 | 0 |
| 1 1 | 0 | 0 | 1 1 | 1 | 0 0 |
Для оцінки ефективності описаного вище методу групування розрядів відзначимо насамперед, що для будь-якої комбінації цифр протягом двох циклів множення може бути не більш одного додавання або віднімання. Таким чином, в гіршому випадку кількість додавань-віднімань дорівнює 0,5п.
Середня кількість додавань-віднімань дорівнює 0,375п. З урахуванням цього середній час множення складає:
- для першого і другого методів множення
;
- для третього і четвертого методів множення
.
Метод множення з послідовним перетворенням цифр множника передбачає послідовний аналіз цифр множника без розбиття на групи. При цьому використовується такі правила перетворення:
- якщо дана цифра неперетвореного множника не збігається із сусідньою праворуч цифрою, сусідня ліворуч цифра є 0 і попередня цифра перетвореного множника є 0, то даний розряд у перетвореному множнику є 1;
- якщо дана цифра неперетвореного множника не збігається із сусідньою праворуч цифрою, сусідня ліворуч цифра є 1 і попередня цифра перетвореного множника є 0, то даний розряд перетвореного множника повинний містити ;
- якщо дана цифра неперетвореного множника збігається із сусідньої праворуч цифрою або якщо попередня цифра перетвореного множника не є нулем, то даний розряд у перетвореному множнику є 0.
Застосовуючи ці правила необхідно враховувати, що старша значуща цифра перетвореного множника може знаходитися в розряді цілих; праворуч і ліворуч від значущих розрядів перетвореного множника завжди передбачаються нулі. Коли в приведеному правилі говориться про "попередні" цифри перетвореного множника, то стосовно до множення від молодших розрядів це відноситься до попередньої молодшої цифри перетвореного множника, а стосовно до множення від старших - до старшої попередньої цифри.
Описане послідовне перетворення розрядів множнику забезпечує під час множення в середньому 0,333п додавань-віднімань. Це найкращий результат, що може бути отриманий для логічних методів прискорення множення.
У здійсненні метод послідовних перетворень ненабагато складніше, ніж метод групування розрядів множника, ефективність же його вище.
При цьому виникають визначеної довжини послідовності чи нулів одиниць, що приводить до необхідності одночасного аналізу декількох розрядів множника і зрушенню на довільне число розрядів.
Похожие работы
... автомата повинна містити певну кількість логічний елементів, що утворюють функціонально повну систему для синтезу необхідної комбінаційної схеми. 1.5 Контроль виконання арифметичних операцій Арифметичні операції виконуються на суматорах прямого, оберненого і доповняльного коду. Припустимо, що зображення чисел зберігаються в машині в деякому коді, тобто операція перетворення в заданий код або ...
... в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). 6. Програмна реалізація Програма розроблена для перетворення чисел з однієї системи числення в іншу.Реалізована в середовищі програмування Borland C++Builder. Лістінг програми: #include <vcl.h> #pragma hdrstop #include "Unit1.h" #include <math.h> #include < ...
... льш прості операції які називаються мікроопераціями тобто кожна операція – це визначена послідовність мікрооперацій. Існують два основні типи керуючих автоматів 1. Керуючий автомат з жорсткою чи схемною логікою. Для кожної операції будується набір комбінаційних схем які в потрібних тактах збуджують відповідні керуючі сигнали. Іншими словами ...
... тову складність операцій у полі, то можна оцінити результуючу бітову складність операцій з многочленами. Щоб відрізняти арифметичну складність від бітової в оцінках ми використовуватимемо символи і . Обчислення значень многочленів. Нехай – довільне кільце. Розглянемо добре відомий алгоритм Руфіні - Горнера для обчислення значень многочлена над кільцем у точці. Останнє число ,і буде шуканим ...
0 комментариев