Состав, структура и схема межотраслевого баланса

1. Состав, структура и схема межотраслевого баланса.

2. Задача и матрица Леонтьева.

Краткое содержание темы

Идея сбалансированности является основой всякого рационального хозяйствования.

Рассмотрим схему народного хозяйства, состоящую из n отраслей, каждая из которых выпускает свой продукт.

В народнохозяйственном механизме все отрасли связаны между собой. Поэтому часть продукции, произведенной i-ой отраслью, потребляется (затрачивается) при функционировании j-ой отраслью. Пусть xij - величина продукции i-ой отрасли, затрачиваемой (используемой) j-ой отраслью. Кроме того, потребителями продукции i-ой отрасли является население и непроизводственные сферы (коммунальные хозяйства, культурно-просветительные учреждения, сфера услуг и т.п.).

Пусть далее, vj - объем конечного продукта j-ой отрасли. Очевидно, он включает dj - непроизводственное потребление (включая вложения в непроизводственные фонды) и bj - накопления производственных фондов.

Пусть далее, wj - общий объем производства j-ой отрасли, тогда имеем следующие соотношения:

, j = 1, 2, ..., n, (3.1)

где – общее промышленное и производственное потребление, далее:

,

где vj - непроизводственное потребление и накопление.

В принципе формула (3.1) представляет математическую модель межотраслевого баланса в сфере потребления.

Отрасль можно анализировать не только с точки зрения распределения ее продукции, но и с точки зрения затрат на производство в данной отрасли. Пусть в этом случае в i-ой отрасли имеются затраты на заработную плату zi , кроме этого в балансе необходимо предусмотреть доход Di (i = 1, 2, ..., n). Тогда баланс по затратам будет иметь для i-ой отрасли следующий вид:

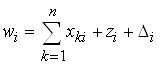, i = 1, 2, ..., n,

т.е. стоимость продукции i-ой отрасли равна стоимости продукции, затраченной от всех n отраслей, плюс заработная плата и доход от реализации продукции этой отрасли.

Введем определение коэффициента прямых затрат в виде соотношения:

 , или  .

Подставляя последнее соотношение в (3.1), получим:

,

или в векторной форме:

w = Aw + v. (3.2)

Пусть себестоимость производства одной единицы продукции j-ой отрасли будет равна cj . Тогда общие народнохозяйственные расходы выражаются соотношением:

.

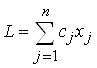Ставится следующая задача оптимизации плана , когда:

,

а линейная форма L обращается в минимум.

Таким образом, приходим к так называемой статической модели межотраслевого баланса.

Очевидно, что условиям задачи может удовлетворять множество наборов значений xi (i = 1, 2, ..., n). Каждый такой набор носит название допустимого решения (стратегии, управления, плана). То решение, которое доставляет минимум целевой функции (линейной форме L) называется оптимальным.

Поиск решения задачи межотраслевого баланса путем обращения матрицы (I - A) в различных аспектах был предложен Леонтьевым В., и в научных кругах задача с матрицей (I - A) называется задачей Леонтьева.

Матрица A получила название матрицы Леонтьева. Матрица (I-A)^-1 называется матрицей коэффициентов полных затрат. Основной результат межотраслевого анализа может быть сформулирован в виде матричного равенства:

w = (I - A)^-1 v . (3.3)

Матрица A называется продуктивной, если матрица  (положительная). Нормой матрицы A назовем максимум сумм элементов ее столбцов. Она обозначается ||A||. Можно доказать, что если A положительная матрица и , причем хотя бы для одного столбца сумма его элементов строго меньше 1, то A будет продуктивной матрицей.

Тема 4. Задачи на смеси

1. Постановка задачи на смеси.

2. Графический метод решения.

3. Общий алгоритм решения задач линейного программирования.

Краткое содержание темы

Задачи на смеси являются одним из показательных классов задач по линейному программированию в области планово-экономических исследований. На примере таких задач могут быть рассмотрены основные методы решения задач линейного программирования как одного из крупных разделов математических методов экономических исследований.

Классическая задача на смеси ставится следующим образом. Из различных видов сырья объемом соответственно b₁, b₂,..., b_m-1, b_m можно изготовить n видов продукции. Пусть цена единицы j-го вида продукции будет c_j и для изготовления единицы j-го продукта требуется затратить i-ый вид сырья в количестве a_ij единиц. Возникает вопрос, какие виды продукции и в каком количестве нужно производить, чтобы получить наибольшую выручку?

Таким образом, нужно определить количество производимой продукции при ограниченных ресурсах, при этом реализация произведенной продукции должна дать максимальную выручку.

Математически описанную задачу можно представить следующим образом.

Пусть  - количество j-ой продукции, тогда стоимость всей произведенной продукции можно выразить функцией:

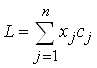 ‑ целевая функция.

Следовательно, в задаче идет речь о достижении максимума целевой функции L на множестве различных допустимых значений . Другими словами, критерием оптимальности задачи является: .

Очевидно, далее, что  ³ 0 для j = 1, 2,..., n. Количество произведенной продукции не может быть отрицательным. Далее, на единицу j-го вида продукции требуется  единиц i-го сырья, т.е. для изготовления  единиц j-го продукта потребуется  единиц i-го сырья.

Так как один и тот же вид сырья может использоваться для производства любого j-го продукта, то суммарные потребности i-го сырья на все j-ые продукты не должны превышать имеющихся ресурсов b₁, b₂, ..., b_m сырья, т.е.

.

Таким образом, приходим к следующей математической задаче.

Найти: 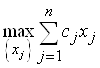 при условии, что  и .

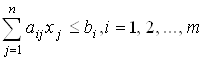Очевидно, что условиям задачи может удовлетворить множество наборов значений x_j, где j = 1, 2, ..., n. Каждый из таких наборов носит название допустимого решения (стратегии, управления, плана). Решение, при котором достигается max целевой функции, называется оптимальным.

Графический метод решения задачи на смеси вытекает из следующих основных свойств задач линейного программирования:

·  существует выпуклый многоугольник (многогранник) допустимых решений;

·  оптимальное решение задачи достигается в одной из вершин многоугольника допустимых решений.

Следовательно, если построить гиперплоскость целевой функции (критерия) нулевого уровня, то, передвигая ее в сторону возрастания значений переменных, можно определить первую или последнюю вершину многоугольника допустимых решений для поставленной задачи, с которой передвигаемая гиперплоскость впервые встречается или покидает область многоугольника. В частном случае гиперплоскость может представлять прямую линию. Соответственно первая вершина встречи будет определять минимальное значение целевой функции, а последняя вершина встречи - максимальное.

Общий алгоритм решения задач линейного программирования

Без ограничения общности имеем следующую задачу линейного программирования:

, (4.1)

.

Найти среди допустимых , j = 1, 2, ..., n, такие, что:

.

Основные шаги решения сформулированной задачи следующие.

1. Находится хотя бы одно из неотрицательных решений .

2. Подставляем в систему полученное решение, в результате чего получаем новую систему, эквивалентную исходной:

.

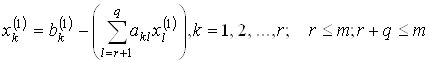3. Подставляем выражения основных переменных в L:

.

4. Применяем последовательность тождественных преобразований к полученной системе и линейной форме до тех пор, пока не исчезнут положительные коэффициенты при переменных в линейной форме, т.е. нарушатся условия ее существования.

После конечного числа указанных шагов (если нет зацикливания) находится оптимальное решение поставленной задачи. В этом заключается суть симплекс-метода.

Возникает вопрос. Как найти хотя бы одно неотрицательное решение системы (4.1)?

Сводим исходную систему (4.1) к виду:

, i = 1, 2, ..., m. (4.2)

Если в этой системе имеется переменная, входящая только в одно уравнение, и коэффициент при ней имеет знак «+», то уравнение можно разрешить относительно этой переменной.

Считаем, что в (4.2) уравнения разрешены относительно всех таких переменных, тогда, сделав перенумерацию, имеем:

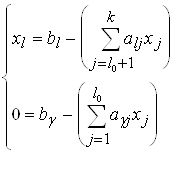(4.3)

l = 1, 2, ..., l₀;  = 1, 2, ..., ₀;

l₀ + ₀ = m; l₀ + k = n; .

Любое уравнение в (4.3), неразрешенное относительно какой-либо переменной, будем называть 0-уравнением.

Для системы (4.3) неотрицательное решение отыскивается последовательными тождественными преобразованиями, удовлетворяющими следующим условиям:

1. Отыскиваем 0-уравнение, у которого свободный член  (если такого свободного члена нет, то значения переменных xl = bl, , l = 1, 2, ..., l0; j = 1, 2, ..., k образуют неотрицательное решение системы (4.3)). Пусть это будет i-ое уравнение.

2. Отмечаем в i-ом уравнении положительный коэффициент .

3. Находим разрешающий элемент  и производим торжествен­ное преобразование (4.3).

4. i-ое 0-уравнение используется до тех пор, пока либо разрешим его, либо придем к несовместимости системы (4.3).

5. После разрешения i-го уравнения отыскиваем следующее 0-уравнение с положительным свободным членом и производим с ним аналогичные действия.

6. Процесс продолжается до тех пор, пока не освободимся от всех 0-уравнений.

В результате можем получить:

а) после конечного числа тождественных преобразований система освободится от 0-уравнений. Тогда система будет совместимой. Совокупность значений переменных, получаемых приравниванием неосновных переменных нулю, а основных - свободным членам в системе, не содержащей 0-уравнений, является неотрицательным решением исходной системы;

б) После конечного числа тождественных преобразований обнаружится, что используемое 0-уравнение превращается в уравнение вида:

,

где , т.е. для всех j - система несовместна;

в) система не освобождается полностью от 0-уравнений, а условия тождественных преобразований не нарушаются. Число 0-уравнений не увеличивается, а некоторые из них имеют по крайней мере один положительный коэффициент в правой части, но разрешающий элемент ему не принадлежит.

Тема 5. Транспортная задача