Требования поступают через одинаковые интервалы времени. Каждый интервал имеет длину a единиц

1. Требования поступают через одинаковые интервалы времени. Каждый интервал имеет длину a единиц.

2. Требования обслуживаются за одинаковые интервалы времени, каждый интервал имеет длину b единиц. При этом, как только закончится обслуживание одного требования, обслуживающее устройство готово к обслуживанию следующего требования.

3. Дисциплина очереди устанавливается по правилу “Первый пришел - первый обслуживается”. Другими словами, ожидающие требования образуют очередь, и, когда обслуживающее устройство освободится, на обслуживание поступает требование, имеющее большее время ожидания.

Определим длину очереди как общее число требований, находящихся на обслуживании и ожидающих в очереди. Представим сформулированную задачу в виде следующей схемы:

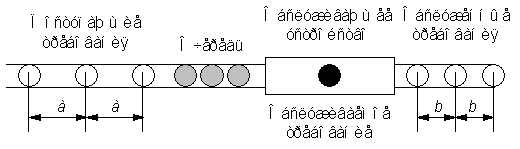
Поведение системы зависит от того, как связаны между собой величины a и b. Возможны три случая: 1) b > a; 2) b = a; 3) b < a. Рассмотрим каждый из этих случаев.

1) Случай b > a. Это значит, что скорость обслуживания 1/b меньше, чем скорость поступления требований 1/a, т.е. требования обслуживаются и покидают систему медленнее, чем прибывают. Следовательно, в этом случае будет образовываться очередь и она будет постоянно возрастать.

2) Случай b = a. Если в очереди нет требований, то первое поступившее требование сразу начнет обслуживаться. Его обслуживание закончится в тот же самый момент, в который поступит на обслуживание следующее требование. Следовательно, требований, ожидающих обслуживания, не будет.

Если же первоначально имеется очередь, то ее длина будет оставаться постоянной.

3) Случай b < a. Это значит, что скорость обслуживания больше, чем скорость поступления требований. Следовательно, какое бы ни было начальное число ожидающих обслуживания требований, длина очереди будет сокращаться до 1 или 0.

Пусть в начале процесса число требований в очереди r ³ 2 (если первоначально есть только одно требование (r = 1), то оно будет обслужено прежде, чем поступят на обслуживание следующие требования, и очередь будет пустой).

В общем случае, пусть имеем r требований, стоящих в очереди перед началом обслуживания. Тогда число требований (N), поступивших после начала процесса обслуживания до тех пор, пока сохраняется очередь, можно определить по формуле:

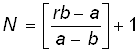, (10.1)

где обозначение [x] означает целую часть числа x. Действительно, очередь будет отсутствовать, если через обслуживающее устройство полностью пройдет N+r требований. Для этого потребуется (N+r)b единиц времени. За это время на обслуживание поступит N требований, так что к поступлению (N+1)-го требования обслуживающее устройство будет свободно и готово обслужить его сразу без всякой очереди. Но (N+1)-е требование поступит на обслуживание через (N+1)a единиц времени, при этом будет выполнено соотношение:

.

Отсюда,

. (10.2)

Докажем, что в полученном соотношении N больше правой части не более чем на 1. Действительно, первое стоящее в очереди требование будет уже обслужено, а первое вновь поступающее на обслуживание требование еще не появится в очереди (a > b). Поэтому справедливо соотношение:

aN  (N+r-1)b или .

Таким образом, если к правой части соотношения  добавим 1, то оно будет тождественно равно правой части соотношения . То есть прибавление 1 к правой части соотношения  приводит его к соотношению  – смысл неравенства меняется на противоположный. Это и требовалось доказать.

Очевидным является то, что N есть целое число. Следовательно, если от правой части в соотношении (10.2) взять целую часть и добавить к ней 1, то, исходя из предыдущих рассуждений, получим для вычисления N выражение (10.1).

Аналогичными рассуждениями и используя (10.1) можно найти, что для вычисления времени, которое необходимо для обслуживания всех ожидающих требований, справедлива формула:

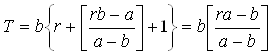. (10.3)

В теории очередей важной функцией является функция времени ожидания обслуживания. Обозначим ее через W(t). Определим W(t) как время, которое необходимо затратить на ожидание обслуживания требования, поступившего в момент времени t (считаем, что t = 0 соответствует началу процесса обслуживания).

Определим формулу для W(t). Легко видеть, что требование, поступившее на обслуживание в момент t ³ T-b (величина T определяется с использованием формулы (10.3)), найдет систему обслуживания пустой или только что освободившейся. Такому требованию не придется стоять в очереди. Требование, поступившее в момент времени t£T-b, найдет впереди себя 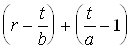 требований, стоящих в очереди, причем первое из них в этот же момент поступит на обслуживающее устройство. Эта величина получается следующим образом:

(начальная (число требований, обслужен- (число поступ-

очередь) - ных к моменту времени t) + лений)

r - + .

Таким образом, время ожидания W(t) для рассматриваемого требования может быть выражено формулой:

. (10.4)

Рассмотрим i-е требование в начальной очереди (0 <i £ r), тогда впереди его будет (i - 1) требований, для обслуживания которых потребуется (i - 1)b единиц времени.

Обобщая полученные результаты относительно функции W(t), получим для нее следующее выражение:

,

где i - номер i-го требования в начальной очереди; требования поступают в моменты времени a, 2a, ...; b = na (n = 1, 2, ...).

Тема 11. Управление запасами

1. Понятие задачи управления запасами.

2. Основная задача управления запасами.

3. Управление запасами в условиях производственных поставок.

4. Управление запасами в условиях дефицита.

Краткое содержание темы

Класс задач по управлению запасами является достаточно специфичным как по разнообразию постановки задач, так и по методам их решения. Здесь успешно применяются методы линейного и динамического программирования, методы теории массового обслуживания и многие другие. В данном разделе рассматриваются простые методы математического анализа для решения задач управления запасами.

Предприятия в процессе своей деятельности делают различные запасы. Запасы - это совокупность предметов (товаров), представляющих собой временно неиспользуемые экономические ресурсы.

Причины создания запасов могут быть различными.

Если в нужный момент производства необходимые материалы или товары не поступают от поставщиков и их нет на складе в запасе (т.е. имеет место дефицит), процесс производства может задержаться или совсем остановиться. Однако, если запасы достаточно велики, то возрастает плата за них и за их хранение.

Таким образом, возникает задача управления запасами, т.е. необходимо выбрать некоторое компромиссное решение по созданию запасов или выработать стратегию управления запасами.

Основные типы принимаемых решений по управлению запасами следующие:

1. Определить какое, количество товара должно быть в запасе.

2. Определить, в какое время необходимо производить пополнение запасов.

В настоящее время существует множество подходов к решению подобного рода задач.

Рассмотрим три простейшие математические модели, включающие:

а) основную модель управления запасами - определение оптимального размера партии;

б) модель производственных поставок;

в) модель, учитывающую штрафы.

Итак, предмет изучения - количество D запаса на складе и время t, для которого рассматривается этот запас, т.е. исследуется функция D = f(t), соответствующая величине запаса в момент времени t. График такой функции называется графиком изменения запаса.

По поводу изменения функции запасов сделаем следующие предположения:

1 .При наличии заявки на товар, он отпускается и D уменьшается. Величина спроса непрерывна во времени.

2. Если D = 0, то имеет место дефицит товара.

3. При поступлении товаров на склад (запасы пополняются) и D увеличивается. Пусть сначала пополнение запасов будет мгновенным, затем допустим, что пополнение идет непрерывно, в течение некоторого интервала времени.

Издержки, связанные с запасами, можно представить следующим образом:

Организационные издержки - расходы, связанные с оформлением и доставкой товаров, необходимые для каждого цикла складирования. Это подготовительно-заключительные операции при поступлении товаров и подаче заявок.

Если запасы нужно пополнить, то на склад завозится очередная партия. Издержки на поставку - организационные издержки.

Количество товаров, поставляемое на склад, - размер партии товаров.

Издержки содержания запасов - затраты, связанные с хранением. Расходы этого рода возникают из-за ренты складирования и амортизации в процессе хранения (товары могут портиться, устаревать, их количество может уменьшаться и т.п.).

Издержки, связанные с дефицитом (штрафы). Если поставка со склада не может быть выполнена, то возникают дополнительные издержки, связанные с отказом. Это может быть реальный денежный штраф, уплачиваемый лицу, делающему заявку на товар, или ущерб, не осязаемый непосредственно (ухудшение бизнеса в будущем, потеря потребителей).

Математическая модель должна учитывать все эти издержки, и цель моделирования заключается в том, чтобы найти такую стратегию управления запасами, при которой суммарные издержки, связанные с запасами, сводились бы к минимальным.

Основная задача

Итак, имеем следующую таблицу параметров модели и предположения (допущения) по изменению их величин.

Название параметра	Обозначение	Единицы измерения	Предположения
Интенсивность спроса	d	Ед-цы товара в год	Спрос постоянен и непрерывен. Весь спрос удовлетворяется.
Организационные издержки	s	$ за одну партию	Организационные издержки постоянны, не зависят от размера партии
Стоимость товара	c	$ за ед-цу товара	Цена ед-цы товара постоянна, имеем только один вид товара
Издержки содержания запасов	h	$ за ед-цу товара в год	Стоимость хранения ед-цы товара в течение года постоянна
Размер партии	q	Ед-ца товара в одной партии	Постоянная величина, поступление мгновенное, как только уровень запаса становится равным 0.

Задача управления: определить значение q, при котором минимизируются годовые затраты.

Рассмотрим график изменения запасов. В соответствии с предположениями этот график имеет вид:

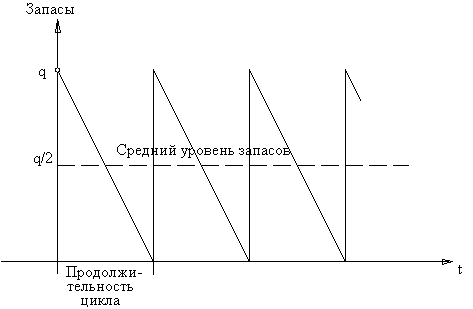
Чтобы полностью удовлетворить годовой спрос d в размере поставки, равном q, нужно за год сделать  поставок. Партия - это поставка.

Средний уровень запасов равен .

Составляем уравнение издержек. Это будет:

.

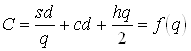Чтобы найти минимум С, считаем функцию f(q) дифференцируемой. Тогда значение q находится из уравнения:

 или ,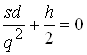

откуда

,

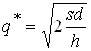где q* - оптимальный размер партии, называемый также оптимальным заказом.

Модель производственных поставок

Рассмотрим теперь модель производственных поставок, когда поступление товаров на склад производится непосредственно с производственной линии, т.е. уже не будет мгновенным (т.е. партия не поставляется в течение одного дня).

Считаем, что заказы поступают непрерывно.

Допущения в таблице остаются такими же за исключением тех, которые касаются поступления продукции. Эта величина теперь будет определяться скоростью производства, p - количество товаров, выпускаемых производственной линией за год.

За каждый цикл изменения запасов на склад поступает q единиц товара. Это количество идет с производственной линии, работающей со скоростью p. Спрос в течение года постоянен и его интенсивность d. Как только уровень запасов станет нулевым, с линии начнет поступать следующее количество товаров. Величина q - размер партии, т.е. количество товара в одной поставке. Описанная картина представлена на следующем графике:

Эффективная скорость пополнения запасов в течение времени поставки равна p - d.

Уравнение издержек:

С = С1 + С2 + С3.

Для С1 имеем следующее. Спрос равен d товаров в год. Следовательно, если одна поставка содержит q - товаров, то за год нужно сделать  поставок, а именно:

.

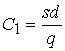Для С2 имеем:

С2 = сd.

Для С3 (затраты на хранение запасов) имеем:

С3 = (средний уровень запасов) × h.

Средний уровень запасов находится следующим образом: