Максимальный уровень RT = (p - d)t, где t ‑ продолжительность поставки

1. Максимальный уровень RT = (p - d)t, где t ‑ продолжительность поставки.

2. pt = q (количество товаров в одной поставке).

Отсюда:

(средний уровень запасов) = (максимальный уровень запасов) = .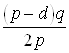

Следовательно:

.

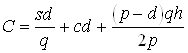Оптимальный размер партии находится из уравнения:

.

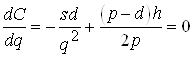Отсюда

 .

Модель, учитывающая штрафы

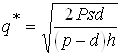Рассмотрим третью модель, которая включает штрафы.

Считаем, что существуют периоды дефицита товаров (нулевые запасы), который покрывается при последующих поставках, и штрафов за несвоевременную поставку.

Пусть по контракту предприятие должно поставить q единиц товара в течение каждого промежутка времени продолжительностью L, за единицу времени поставляется d единиц товара (q = Ld). Значения q и L постоянны. Пусть далее в начале каждого периода L предприятие делает запас единиц товара y < q, т.е. в течение периода наблюдается дефицит товара и некоторое время поставок не будет. Невыполненные заявки будут накапливаться до максимальной величины q-y, но они будут удовлетворены, как только поступит следующая партия товаров в количестве q.

За несвоевременную поставку на предприятие налагается штраф, величина которого зависит от того, на сколько была задержана поставка. (Иногда выгоднее заплатить штраф, чем расходовать средства на хранение запасов, превышающих величину у).

Задача управления в этом случае состоит в том, чтобы выбрать такое значение у, которое ведет к минимизации всех затрат.

Рассмотрим издержки одного цикла. Общие издержки в модели пусть будут:

h - издержки хранения единицы товара за единицу времени;

p - затраты на штраф в расчете на единицу товара за один день отсрочки.

График изменения запасов будет:

Находим издержки одного цикла.

Для С1 имеем следующее. Товары находятся на складе в течение периода АВ, средний уровень запасов за этот период равен у/2. Продолжительность периода АВ равна у/d. Отсюда:

.

Для С2. Штраф выплачивается за невыполнение поставок в течение периода . Общее количество "товаро-дней", за которые налагается штраф, равно площади DBCD. Но

SD_BCD = .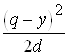

Отсюда:

.

Cледовательно:

.

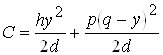Оптимальное значение у находим из условия:

,

отсюда:

, .

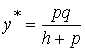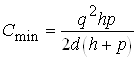Таким образом, взяв значение у* в качестве уровня запасов в начале каждого цикла, при условии, что невыполненные заявки в дальнейшем будут удовлетворены, сведем суммарные расходы С к минимуму.

Тема 12. Методы экспертных оценок

1. Основные понятия методов экспертных оценок.

2. Понятие множества неулучшаемых альтернатив.

3. Основные подходы к поиску предпочтительных экспертных оценок.

4. Основные этапы подготовки и проведения экспертных оценок.

Краткое содержание темы

Как показывает опыт практической экономической деятельности, особенно в той ее части, которая связана с управлением в области экономики, где существенную роль играет такой аспект действий как принятие решений, одного арсенала формально решаемых задач в большинстве случаев бывает недостаточно. В таких случаях приходится обращаться к компетентным специалистам, в интуиции которых сосредоточен иррациональный опыт хозяйствования и управления и рационального познания экономики в виде формализованных моделей. Такие специалисты, которые в “совершенстве” владеют определенной проблемой, называются экспертами. Результатом их труда являются различного рода оценки, рекомендации и предложения. При привлечении значительного количества экспертов к выработке вариантов решений встает задача обработки результатов работы экспертов. Здесь опять встает проблема использования формализованных методов - методов экспертных оценок.

Как правило, результат работы каждого эксперта представляется в виде альтернативы, поскольку безальтернативные результаты работы различных экспертов могут быть представлены в виде результата работы коллективного эксперта и каких-либо методов обработки таких результатов не требуется.

Таким образом, методы экспертных оценок можно рассматривать как методы преодоления альтернатив.

Технология проведения экспертных оценок включает в себя три составляющие:

·  интуитивно-логический анализ;

·  формирование и выдача характеристик (собственно оценка, результат решения);

·  обработка результатов экспертизы ‑ различных альтернатив.

Интуитивно-логический анализ строится на логическом мышлении (возможно на использовании формализованных экономико-математических моделей) и интуиции экспертов, их знании и опыте. В принципе это - индивидуальный процесс, в котором каждый эксперт проводит сравнительный анализ различных альтернатив решения, их количественные и качественные измерения (оценки) в разных условиях.

Формирование и выдача результатов экспертизы является, как правило, многокритериальной задачей, решение которой не сводится к достижению какой-либо одной цели.

На заключительном этапе, когда в общей экспертизе участвует не один эксперт (не одна группа экспертов), полученные от экспертов результаты используются для обобщения и формирования результирующей характеристики проблемы явления, объекта в виде обобщенной итоговой оценки. В этом процессе используется вся мощь методов экспертных оценок. Именно на этом этапе осуществляется процесс преодоления альтернатив.

С преодолением альтернатив связаны два фундаментальных понятия:

·  множество различных вариантов решений (альтернатив), обозначим его {X};

·  принцип выбора, т.е. правила, по которым осуществляется выбор, обозначим его через Ф.

Задача экспертизы может быть записана в следующем виде:

, (12.1)

где {X*} - выбранные альтернативы.

В зависимости от степени формализации введенных понятий различают следующие типы задач:

1. Задача оптимального выбора - если множество {X} однозначно определено, а принцип выбора Ф формализован (т.е. может быть описан, передан и результаты его применения к элементам из {X} не зависят от субъективных условий).

2. Задача выбора (просто) - если множество {X} однозначно определено, но принцип выбора Ф не может быть формализован или просто фиксирован. Выбор зависит от того, кто и на основе какой информации его делает.

3. Общая задача выбора - если множество {X} не имеет определенных границ (может дополняться и видоизменяться), а принцип выбора Ф неформализуем или даже не фиксирован. В этом случае разные субъекты могут выбирать в качестве решения те альтернативы, которые другими субъектами и не рассматривались, а один и тот же субъект при использовании одного и того же принципа выбора (неформализованного, но для него существенного) может изменять свое решение при обнаружении им новой альтернативы.

С формальной точки зрения может показаться, что последняя задача является настолько расплывчатой, что теряет смысл - т.е. не знаем из чего выбирать и чем руководствоваться при выборе. Однако именно эта задача с некоторыми естественными ограничениями наиболее характерна для практики.

Каковы же эти естественные ограничения?

Во-первых, в реальной задаче, как правило, всегда существует так называемое начальное множество альтернатив {X⁽⁰⁾}, на основе которого приступают к принятию решения. В дальнейшем это множество изменяется, но можно считать, что на любой момент процесса экспертизы мы имеем дело с фиксированным множеством {X⁽ⁱ⁾}:

.

Во-вторых, подразумевается, что альтернатива X  из множества всех мыслимых альтернатив {X^(M)} может быть оценена с точки зрения полезности включения ее в множество {X}. Это делается при помощи некоторого вспомогательного принципа выбора Ф^(M). Чаще всего этот принцип неформализован. Таким образом, и само множество {X}, вообще говоря, является итогом экспертной оценки, которую можно представить в виде:

. (12.2)

В-третьих, считается, что существуют хотя бы неформализованные принципы выбора, относящиеся к принимаемому решению. Часто (но не всегда) есть уверенность, что применение таких принципов различными субъектами дает пересекающиеся или в каком-то смысле близкие результаты.

Перечисленные условия дают уверенность в том, что общая задача выбора 3 может быть решена в той или иной степени обоснованно.

Практические пути решения не полностью определенных задач 3 и 2 состоят в использовании для этой цели ряда задач с фиксированным, но меняющимся от задачи к задаче множеством {X} и фиксированным (хотя необязательно формализованным) принципом выбора Ф. Это происходит с применением ряда приемов. Первый из них - организация итерационного процесса решения набора задач вида 1. Она состоит в начальном решении одной или нескольких формализованных задач, анализе результатов их решения, назначения измененных множеств альтернатив {X} и измененных принципов выбора Ф, нового решения набора задач и т.д. до получения удовлетворительного результата. Другой прием заключается в решении ослабленного варианта задачи 1, когда принцип выбора формализован не полностью, а допускает участие экспертов, каждый из которых по-своему, обычно неформальным образом, фиксирует принцип Ф. В этом случае каждый из экспертов порождает свою задачу типа 1, а решение исходной задачи формируется на основе их решений. Следующей прием близок к первому. Здесь задачам типов 3 или 2 сопоставляется некоторый аналог, выбранный среди задач типа 1, а полученное решение служит основой для неформального поиска решения требуемой задачи.

Таким образом, задача типа 1 является ядром в процессе решения других типов задач.

Общепринятым принципом, который облегчает принятие решения, является переход от сравнения альтернатив в целом к сравнению их отдельных частей и свойств (аспектов, характеристик, признаков, преимуществ и т.п.). Основная идея такого перехода состоит в том, что в отношении отдельной части и (или) отдельного свойства существенно легче сказать, какая из альтернатив предпочтительней.

Но сравнение по отдельным частям (свойствам) порождает серьезные проблемы обратного перехода к требуемому сравнению альтернатив в целом.

Выделение частей и/или свойств альтернатив является не чем иным, как декомпозицией альтернативы.

Сравнение альтернатив по отдельным частям (свойствам) может быть выполнено следующими способами:

1) на основе парного (реже группового) сравнения альтернатив по данному свойству;

2) на основе введения естественных числовых характеристик выделенного свойства;

3) на основе введения искусственных числовых характеристик выделенного свойства.

Рассмотрим эти способы сравнений.

Парное сравнение. Пусть для двух альтернатив X₁ и X₂ из множества {X} можно произвести выбор наиболее предпочтительной по данному свойству. Способ выбора в общем случае не конкретизируется. Если он связан с использованием числовых характеристик, то такая ситуация относится к способу (2) или (3). Возникает вопрос: «Существует ли объективный способ выбора, не связанный с числами?» С практической точки зрения можем считать вполне объективными и не основанными на числовых характеристиках такие утверждения: “Этот вариант размещения пунктов потребления более предпочтителен для развертывания широкой торговли”, “Этот человек более удачно справится с поставленной задачей” и т.п.

С формальной точки зрения для альтернатив X₁ и X₂ из {X} вводится бинарная операция сравнения по признаку (свойству) R. Запись этого события можно представить в виде:

X₁RX₂, (12.3)

что означает: альтернатива X₁ предпочтительней (или “не хуже”) альтернативы X₂ по признаку R. Указанная операция может быть применена как к любой паре (X₁, X₂) из {X}´{X}, так и не ко всем из них. В последнем случае допускается, что относительно некоторых пар нельзя сделать выбор, как говорится, элементы множества {X} только частично сравнимы по признаку R.

Для операции R естественной является аксиома транзитивности, которая заключается в том, что из X₁RX₂ и X₂RX₃ следует X₁RX₃.

На основе бинарного сравнения может быть выполнена специальная операция ранжирования (упорядочивания). Результатом такой операции является то, что альтернативы в зависимости от их свойства R располагаются в определенном порядке: от наиболее до наименее предпочтительной. Математически эта операция эквивалентна определенной перестановке.

Введение числовых характеристик. Сравнение элементов на основе сопоставления им числа представляется наиболее аргументированным способом выбора. Необходима только уверенность, что выполненное сопоставление объективно. Как правило, это имеет место, если числовая характеристика обладает физическим смыслом. Можно утверждать, что в процессе экспертной оценки следует стремиться довести декомпозицию экспертируемого объекта до уровней, на которых возможны числовые оценки.

Свойства, для которых существуют объективные численные характеристики, принято называть критериями.

Таким образом, получение набора критериев - наилучший итог процесса декомпозиции. Он настолько привлекателен, что к его аналогу прибегают и тогда, когда естественные числовые характеристики отсутствуют. В этом случае вводятся искусственные оценки типа баллов. Они проставляются экспертами, каждый из которых может исходить из своего неформального принципа выбора. Этим решается задача количественной оценки качественных сторон явления или проблемы. Примерами таких оценок могут служить: коэффициент трудового участия, разрядная сетка рабочих специальностей, процент износа механизма.

Искусственные оценки практически непрерывно переходят в естественные. Однако в ряде случаев процесс перехода осложнен, и тогда эксперт обладает определенной свободой выбора. Это имеет место при присвоении рабочих разрядов, назначении коэффициентов в эмпирически подобранные зависимости, определении отдельных внутренних параметров и т.п.

Дополнительным приемом, который в ряде случаев облегчает все приведенные выше способы сравнения, является распределение элементов по подмножествам. Тогда любая альтернатива X из {X} в целом или по своему свойству R относится к одному из фиксированных подмножеств {X₁}, {X₂}, ... . Такое распределение называется задачей классификации и может как сводиться к перечисленным способам сравнения, так и быть самостоятельной задачей. Частным случаем классификации является деление свойств альтернатив по степени важности в данной задаче. Смысл этого приема состоит в сужении числа свойств, принимаемых во внимание в первую очередь.

Процесс декомпозиции альтернативы является мощным орудием анализа проблемы, оценки ее отдельных свойств. Однако, смысл любой экспертизы заключается в оценке проблемы в целом, т.е. в обобщенной оценке. Процесс обобщения отдельных экспертных оценок, полученных на этапе декомпозиции альтернативы, носит название композиции оценок и сравнений. Сразу следует отметить, что непростой процесс анализа альтернативы на этапе декомпозиции намного усложняется на этапе композиции.

Множество неулучшаемых альтернатив получило название множества Парето.

Ясно, что точки, не принадлежащие множеству Парето, не могут претендовать на то, чтобы считаться лучшей альтернативой.

Выделение множества Парето - это только первый шаг в сравнении альтернатив. Вообще можно ограничиться только этим шагом и считать лучшими все те альтернативы, которые попали в это множество. Однако в большинстве случаев проведения экспертиз требуется в итоге выбрать только одну альтернативу. Как действовать на множестве Парето?

Приемов такого выбора, основанных на столь же естественных предположениях, которые привели к выделению множества Парето, к сожалению не существует. Здесь часто используются специфические, порой спорные приемы.

Выше рассмотрены основные методы экспертных оценок, которые могут применяться в ходе проведения экспертиз и обработки их результатов. Но, как организуется экспертиза? Формы организации экспертизы могут быть достаточно разнообразными и многочисленными в зависимости от условий проведения экспертизы и контингента привлекаемых экспертов. Классические формы работы с экспертами - это заполнение анкет (таблиц), интервью, запрос аналитического отчета.

Первая из этих форм является наиболее распространенной. В вопросники как правило включаются простые вопросы, которые для ответа не нужно разбивать на отдельные части. Интервью предпочтительнее анкет, если оно проводится высококвалифицированным специалистом, способным подстроиться под интервьюируемого, помочь ему выбрать более обоснованные ответы, но одновременно не привнести в них свое мнение.

Следует иметь в виду, что человек более обосновано приводит качественные ответы, чем количественные.

Экспертизы различаются и по форме взаимодействия экспертов. Обмен мнениями может быть свободным, регламентированным и недопустимым. Все эти способы имеют свои преимущества и недостатки.

При свободном общении ряд экспертов может доминировать над другими, и чье-то мнение может оказаться неучтенным.

Регламентированное общение требует более сложной организации; его известный вид - это метод “мозговой атаки”, когда сначала мнения высказываются без обсуждения и только через некоторое время дискутируются, как правило, под руководством хорошо подготовленного ведущего.

Изолированная работа с экспертами чревата попаданием в дальнейшую обработку искаженных или просто неверных оценок, которые могли бы быть выявлены и изменены при свободном или регламентированном способе.

Причинами неудовлетворительных ответов могут быть нарушения целого ряда требований к экспертам - от неполной компетентности и предвзятости до неспособности решать нестандартные задачи и предвидеть неочевидные последствия.

Предполагается, что правильно обработанное коллективное мнение экспертов более достоверно и надежно, чем индивидуальные мнения отдельных экспертов, и что истинная величина изучаемого явления находится внутри диапазона оценок группы экспертов. Надежность экспертных оценок определяется в первую очередь подбором специалистов-экспертов, их информированностью в изучаемых проблемах, а также возможностью математико-статистической обработки полученных результатов экспертизы.

В подборе экспертов могут быть применены разные подходы, наиболее надежным из них является статистический подход.

Статистический подход к подбору экспертов состоит в проверке эрудиции и аналитических способностей эксперта, а также проверки точности его прошлых оценок.

Интересной реализацией получения обобщенной экспертной оценки, учитывающей указанные особенности организации и проведения экспертиз, является метод Дельфы.

Этот метод представляет ряд последовательно осуществляемых процедур, направленных на выявление группового мнения по той или иной проблеме. Метод получил наименование по названию города Дельфы, ставшего известным из-за прорицателей-оракулов, живших в нем и предсказывающих будущее. Пророчества обнародовались после тщательного обсуждения на совете дельфийских мудрецов.

Метод Дельфы представляет обобщение оценок экспертов, касающихся прежде всего перспектив развития. Особенность метода состоит в последовательном анонимном индивидуальном опросе экспертов, исключающем их непосредственный контакт для уменьшения группового влияния, возникающего при совместной работе экспертов и состоящего в приспособлении к мнению большинства. Работа проводится в несколько этапов. Результаты первого этапа подвергаются статистической обработке. Выявляются преобладающие суждения экспертов и сближаются их точки зрения. Всех экспертов, оценки которых находятся в границах согласованности, знакомят с обоснованиями причин расхождений суждений тех экспертов, оценки которых выходят за указанные границы. Эксперт может изменить свое суждение. Для выявления этого проводится второй тур и т. д.

Метод Дельфы дает возможность улучшить простое усреднение оценок экспертов.

Итак, теперь можно перечислить основные этапы подготовки и проведения экспертизы. Они включают:

·  постановку задачи (проблемы), подлежащей экспертизе;

·  подбор и выбор экспертов;

·  выполнение экспертизы;

·  получение обобщенной экспертной оценки;

·  формирование и оформление результатов экспертизы.

Для примера представим название некоторых задач и проблем, в решении которых применяются методы экспертных оценок.

Это:

·  распределение различных видов ресурсов с установлением приоритетности;

·  установление номенклатуры подлежащих выполнению работ для достижения определенных целей в условиях ограничений по различным ресурсам;

·  установление удельных ресурсных затрат на выполнение каких-либо работ, норм расхода материалов, нормативной трудоемкости изготовления изделия и его составляющих, стоимости отдельных этапов научно-исследовательских и опытно-конструкторских работ;

·  установление возможных и допустимых границ колебания экономических показателей;

·  установление параметров календарно-плановых нормативов, размеров партий запуска-выпуска изделий (деталей), величины заделов;

·  определение перспективных направлений развития производственной системы, организационно-функциональной структуры;

·  многокритериальная оценка деятельности предприятия;

·  определение последовательности выполнения работ;

·  научно-техническое и экономическое прогнозирование.

Процесс подготовки и проведения экспертизы сопряжен с процессом обработки огромных объемов информации с использованием громадного арсенала экономико-математических средств, методов и моделей. Поэтому получение более достоверных и надежных результатов экспертизы на современном этапе развития программно-технических средств не мыслим без привлечения в процесс экспертирования современных электронно-вычислительных комплексов.

Появление интерактивных режимов функционирования в программно-технологических комплексах дает прекрасную возможность оптимально сочетать неформализуемую интуитивную деятельность, присущую человеку, с неограниченными возможностями ЭВМ по решению формализованных задач.

В настоящее время разработан достаточно представительный набор программных средств типа экспертных и логико-расчетных систем (оболочек), позволяющих за приемлемо обозримое время настроиться на решаемый класс экспертных задач, доведя их до уровня “дружественного” общения между человеком и машиной. Существенной особенностью таких систем является так называемая база знаний, построенная на основе формализуемой части труда экспертов по определенным и конкретным проблемам. Некоторые из этих систем доведены до такого “совершенства”, что позволяют проводить экспертные оценки без участия экспертов-специалистов, которые могут привлекаться только в отдельных случаях, когда система начинает давать значительные сбои.

ДОПОЛНИТЕЛЬНАЯ ТЕМАТИКА   Тема А. Элементы теории вероятности

1. Понятие вероятности. Общие свойства вероятности.

2. Основные формулы теории вероятности.

3. Понятие случайной величины. Дискретная и непрерывная случайная величина.

4. Понятие распределения случайной величины. Основные законы распределения.

Краткое содержание темы

Изложение содержания данной темы в настоящей работе не представляется целесообразным, так как его можно без труда найти в широком круге литературных источников, в том числе тех, которые перечислены в данной работе.

  Тема Б. Нелинейное программирование

1. Постановка общей задачи нелинейного программирования.

2. Метод множителей Лагранжа.

3. Выпуклое программирование.

4. Градиентные методы.

5. Метод штрафных функций.

Краткое содержание темы

Постановка общей задачи нелинейного программирования состоит в следующем. Определить максимум (минимум) значения функции:

f(x₁, x₂, ..., x_n) (Б.1)

при условии, что переменные удовлетворяют соотношениям:

, (Б.2)

где, f и g_i некоторые известные функции, b_i - заданные числа.

Решение этой задачи X * = (x₁*, x₂*, ..., x_n*), удовлетворяющее (Б.1) и (Б.2), такое, что для любого другого X = (x₁, x₂, ..., x_n), удовлетворяющего (Б.2), имеем:

f(x₁*, x₂*, ..., x_n*) ³ f(x₁, x₂, ..., x_n) - для задачи максимизации;

f(x₁*, x₂*, ..., x_n*) £ f(x₁, x₂, ..., x_n) - для задачи минимизации.

Соотношения (Б.2) называются системой ограничений. Условия неотрицательности переменных могут быть заданы непосредственно. В евклидовом пространстве E ⁿ (Б.2) определяет область допустимых решений поставленной задачи (в отличие от задач линейного программирования эта область может быть не выпуклой).

Если область допустимых решений определена, то нахождение решения задачи (Б.1)-(Б.2) сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (наинизшего) уровня: f(x₁, x₂, ..., x_n) = h.

Эта точка может быть как на границе, так и внутри области.

Процесс решения задачи в геометрической интерпретации включает этапы:

·  определение области допустимых решений, соответствующих (Б.2) (если она пуста, то решений задачи - нет);

·  построение гиперповерхности f(x₁, x₂, ..., x_n) = h;

·  определение гиперповерхности наивысшего (наинизшего) уровня или установление неразрешимости задачи из-за неограниченности (Б.1) сверху (снизу) на множестве допустимых решений;

·  нахождение точки области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня и определение в ней значения (Б.1).

Метод множителей Лагранжа

Общая постановка задачи состоит в нахождении максимума (минимума) функции: f(x₁, x₂, ..., x_n) при условии: g(x₁, x₂,...,x_n) = b_i , i = 1, 2, ..., m.

Условия неотрицательности x_j могут отсутствовать. Имеем задачу на условный экстремум - классическая задача оптимизации.

Задача решается следующим образом. Вводят набор переменных l_i (i = 1, 2, ..., m) - множителей Лагранжа и составляют функцию:

.

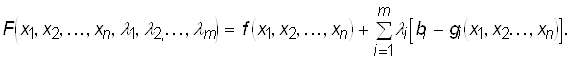Далее определяют частные производные:

 (j = 1, 2, ..., n) и , (i = 1, 2, ..., m).

На следующем шаге рассматривают систему n + m уравнений:

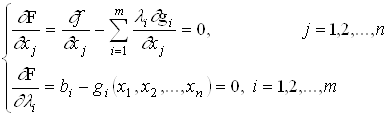
Любое решение этой системы определяет точку , в которой может иметь место экстремум функции f (x₁, x₂, ..., x_n). Таким образом, разрешив построенную систему, определяют все точки, в которых функция f может иметь экстремум. Дальнейшее исследование идет как в случае безусловного экстремума.

Итак, этапы решения задачи нелинейного программирования методом множителей Лагранжа заключаются в следующем:

1.Составляют функцию Лагранжа.

2.Находят частные производные функции Лагранжа по x_j и l_i и приравнивают их 0.

3.Решая полученную систему, находят точки, в которых целевая функция задачи может иметь экстремум.

4.Среди точек, подозрительных на экстремум, находят точки, в которых достигается экстремум, вычисляют значения f(x₁, x₂,...,x_n) в этих точках и среди них выбирают те, которые удовлетворяют условиям задачи.

Выпуклое программирование

Суть общей постановки задачи состоит в определении максимального (минимального) значения функции:

f(x₁, x₂, ...,x_n)

при условиях:

g_i(x₁, x₂, ..., x_n) £ b_i (i = 1, 2, ..., m), x_j ³ 0 (j = 1, 2, ..., n).

Универсальных методов решения поставленной задачи в общем виде не существует. Однако, при определенных ограничениях решение этой задачи может быть найдено.

Несколько определений.

Функция f(x₁, x₂, ..., x_n) на выпуклом множестве X называется выпуклой, если для любых двух точек X₂ и X₁ из Xи любого 0 £ l £ 1, выполнено соотношение:

f[lX₂ + (1 - l)X₁] ³ lf(X₂) + (1 - l)f(X₁).

Множество допустимых решений удовлетворяет условию регулярности, если существует хотя бы одна точка X_i этой области такая, что g_k(X_i) < b_k (k = 1, 2, ..., m).

Задача выпуклого программирования возникает, если функция f является вогнутой (выпуклой), а g_i - выпуклы.

Любой локальный максимум (минимум) является глобальным максимумом (минимумом). Наиболее характерным методом решения задач выпуклого программирования является метод множителей Лагранжа. При этом точка (X₀, L₀) называется седловой точкой функции Лагранжа, если:

F(x₁, x₂, ..., x_n, ) £ F()£

£ F(), для всех x_j ³ 0 и l_i ³ 0.

Для задачи выпуклого программирования, множество допустимых решений которой обладает свойством регулярности, точка X₀ = () является оптимальным решением тогда, когда существует такой вектор L₀= (), что точка (X₀, L₀) является седловой точкой функции Лагранжа, построенной для исходной задачи.

Для задачи определения максимума, условиями седловой точки будут:

(частные производные берутся в седловой точке).

Для задачи нахождения минимума седловая точка определяется соотношениями:

F() £ F()£
£ F().

Условия седловой точки в этой задаче представляются в виде:

,

.

Градиентные методы

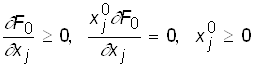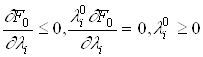Градиентными методами можно найти решение любой задачи нелинейного программирования. Однако в общем случае эти методы позволяют найти точку локального экстремума. Наиболее целесообразным является использование этих методов для решения задач выпуклого программирования, где всякий локальный экстремум является глобальным.

Суть метода заключается в том, что начиная от некоторой точки X^(k) осуществляется последовательный переход к другим точкам до тех пор, пока не будет получено приемлемого решения исходной задачи. Методы можно разделить на две группы.

Первая группа, когда исследуемые точки не выходят за пределы области допустимых решений (здесь используется метод Франка-Вулфа).

Вторая группа, когда эти точки не обязательно входят только в область допустимых решений, однако в итерационном процессе такие точки будут. (Здесь используется метод штрафных функций и метод Эрроу-Гурвица).

Нахождение решения идет итерационным процессом до тех пор, пока градиент функции f(x₁, x₂, ..., x_n) в очередной точке X^(k+1) не станет равным 0, или пока | f(X^(k+1)) - f(X^(k)) |< e, где e достаточно малое положительное число. Эту величину часто называют точностью полученного решения.

Метод Франка-Вулфа

Найти максимум вогнутой функции: f(x₁, x₂, ..., x_n), при условии:

.

Здесь имеем линейные неравенства. Эта особенность является основой для замены в окрестности исследуемой точки нелинейной функции линейной, тогда решение исходной задачи сводится к последовательному решению ряда задач линейного программирования.

Начинается процесс решения с определения точки, принадлежащей области допустимых решений. Пусть это точка X^(k). В ней вычисляют градиент функции f:

Ñf(X^(k)) =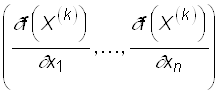

и строят линейную функцию:

F = .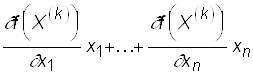

Находят максимум функции F при сформулированных ограничениях. Пусть решение этой задачи Z(k). Тогда за новое допустимое решение принимают:

X^(k+1) = X^(k) + l_k(Z^(k) - X^(k)),

где l_k ‑ некоторое число, называемое шагом вычислений (0 £ l_k £ 1). Число l_k - произвольное и выбирают его так, чтобы значение функции в точке X^(k+1) , зависящее от l_k, было максимальным. Для этого надо найти решение уравнения 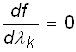 и выбрать его наименьший корень. Если корни уравнения больше 1, то берется l_k = 1. Затем определяют X^(k+1) и f(X^(k+1)) и выясняют необходимость перехода к точке X^(k+2). Если такая необходимость имеется, то в точке X^(k+1) вычисляют градиент целевой функции и переходят к соответствующей задаче линейного программирования и решают ее. Определяют координаты точки X^(k+2) и необходимость дальнейших вычислений. После конечного числа шагов получают с необходимой точностью решение исходной задачи.

Итак, этапы решения задачи методом Франка-Вулфа заключаются в следующем:

1. Определяют одно из допустимых решений.

2. Находят градиент функции f в точке допустимого решения.

3. Строят функцию F и находят ее максимальное значение при условиях исходной задачи.

4. Определяют шаг вычислений.

5. По формуле X^(k+1) = X^(k) + l_k(Z^(k) - X^(k)) находят следующее допустимое решение.

Проверяют необходимость перехода к следующему допустимому решению. В случае необходимости переходят к этапу 2, если такой необходимости нет, то приемлемое решение найдено.

Метод штрафных функций

Пусть имеем вогнутую функцию f(x₁, x₂, ..., x_n). Необходимо найти максимум этой функции при условиях: g_i(x₁, x₂, ..., x_n) £ b_i, (i = 1, 2, ...,m), x_j ³ 0, где g_i - выпуклые функции.

Строится функция: F (x₁, x₂, ..., x_n) = f (x₁, x₂, ..., x_n)+H (x₁, x₂, ..., x_n), где функция H(x₁, x₂, ..., x_n) определяется системой ограничений и называется штрафной функцией. Она может быть построена многими способами. Чаще всего эта функция строится в ви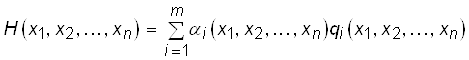де:

, где

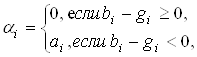a_i ‑ весовые коэффициенты,

q_i = b_i - g_i .

Используя H, последовательно переходят от одной точки к другой до тех пор, пока получится приемлемое решение. При этом координаты последующей точки находят по формуле:

 (Б.3)

Из (Б.3) следует, что если предыдущая точка находится в области допустимых решений, то второе слагаемое в квадратных скобках равно 0, и переход к последующей точке определяется только градиентом целевой функции. Если же предыдущая точка не принадлежит области допустимых решений, то за счет указанного слагаемого на последующих итерациях достигается возвращение в область допустимых решений. При этом, чем меньше  _i, тем быстрее находится приемлемое решение, но точность определения решения снижается. Поэтому в начале  _i берут малым, постепенно увеличивая.

Итак, процесс решения включает этапы:

1.  Определяют исходное допустимое решение.

2.  Выбирают шаг вычислений.

3.  Находят по всем переменным частные производные от целевой функции и функций, определяющих область допустимых решений задачи.

4.  По (Б.3) определяют координаты точки - возможное новое решение.

5.  Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если не удовлетворяют, то переходят к следующему этапу. Если координаты найденной точки определяют допустимое решение задачи, то исследуют необходимость перехода к последующему решению. Если такой переход необходим, то переходят к пункту 2, иначе решение найдено.

6.  Устанавливаются значения весовых коэффициентов и переходят к этапу 4.