Вводится так называемое системное время, которое моделирует ход времени в реальной системе

4. Вводится так называемое системное время, которое моделирует ход времени в реальной системе.

5. Формализованным образом задаются необходимые феноменологические свойства систем в целом и отдельных ее частей. (Часто эти свойства не могут быть обоснованы на современном уровне знаний, а опираются на опыт - длительное наблюдение за поведением системы). Иногда одно такое свойство оказывается эквивалентным множеству сложных математических соотношений и с успехом их заменяет, что, конечно, требует глубокого знания системы.

6. Случайным параметрам, фигурирующим в модели, сопоставляются некоторые их реализации, сохраняющиеся в течение одного или нескольких тактов системного времени. Далее отыскиваются новые реализации.

Как правило, пятый и шестой этапы наиболее просто осуществимы на ЭВМ, поэтому имитационные модели обычно реализуются с использованием специализированных программ, описывающих функционирование отдельных блоков и правила взаимодействия между ними.

Использование реализаций случайных величин требует многократного повторения экспериментов с моделью с последующим статистическим анализом полученных результатов.

Под имитационным моделированием будем понимать пошаговое моделирование поведения объекта с помощью ЭВМ. Это означает, что фиксируются определенные моменты времени t₁,t₂,...,t_n, и состояние модели определяется (вычисляется на ЭВМ) последовательно в каждом из этих моментов времени. Для реализации этого необходимо задать правило (алгоритм) перехода модели из одного состояния в следующее, т.е. преобразование: , где Y_i - состояние модели в i-й момент времени.

Пусть, как обычно, состояние модели определяется вектором: , т.е. m - числами, состояние среды вектором: , n - числами, а состояние управления вектором: , q - числами.

Тогда имитационная модель определяется оператором F, с помощью которого можно определить состояние модели в последующий момент времени, т.е. определить вектор Y_i+1, зная состояние модели в предыдущий момент времени Y_i и значения Х_i+1 и U_i+1, т.е. .

Таким образом, в имитационной модели состояние модели определяется рекуррентно на каждом шаге, исходя только из предыдущего шага. Этот алгоритм можно записать в виде рекуррентной формулы:

,

где F - оператор имитаций изменения состояния модели. Он и определяет имитационную модель объекта.

Можно рассмотреть частный случай имитационной модели под воздействием окружающей среды в виде:

.

Но имитационное моделирование (или модели) тем и хорошо, что позволяет учитывать неконтролируемые факторы Е объекта, т.е. его стохастичность, в этом случае модель можно представить рекуррентным соотношением вида:

, i = 1,...,N, (9.1)

где необходимо знать, каким образом фактор Е влияет на состояние Y объекта, т.е. следует хорошо разобраться в объекте и указать точно, как входит неконтролируемый фактор Е в оператор объекта с тем, чтобы эти данные отразить в операторе F объекта. Для работы с такой моделью необходимо знать конкретные значения фактора E, который, как известно, ненаблюдаем. Возникает противоречие, которое решает так называемый метод Монте-Карло. Собственно, как правило, он и является основным методом имитации.

Для реализации метода Монте-Карло необходимо знать некоторые статистические свойства фактора Е (например, закон его распределения). Эти свойства, вообще говоря, могут зависеть от Y, X и U. Располагая этими сведениями, можно моделировать ненаблюдаемый фактор в виде случайных рядов:

, j = 1, 2, ..., N,

где индекс внизу соответствует дискретному времени, а верхний ‑ номеру моделируемого ряда (всего моделируется N таких статистически эквивалентных рядов). Естественно, ни один из этих рядов не является точной реализацией действительности, но каждый имеет такие же статистические свойства, что и реальный. Именно поэтому ряды  позволяют исследовать статистические свойства модели (9.1).

Так поведение модели " в среднем" описывается как:

, ,

где Y_i^j - j-я реализация поведения модели в i-ый момент времени:

 i=1,2,....,N.

Дисперсия выхода модели вычисляется по формуле:

.

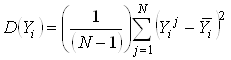Таким образом, метод Монте-Карло позволяет оценить статистические свойства поведения объекта путем вероятностного "разыгрывания" поведения модели, причем одна реализация поведения отличается от другой различными значениями ненаблюдаемого фактора Е.

В сущности методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он становится только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета.

В задачах исследования операций метод Монте-Карло применяется в трех основных ролях:

1. Моделирование сложных, комплексных объектов и операций, где присутствует много взаимодействующих случайных факторов.

2. Проверка применимости более простых аналитических методов и выяснений условий их применимости.

3. В целях выработки поправок к аналитическим формулам "типа эмпирических формул" в технике.

Таким образом, этот метод является своеобразным ОТК математических методов. При этом статистические модели не требуют серьезных допущений и упрощений. В такую модель вписывается все, что угодно - любые законы распределения, любая сложность системы, множественность ее состояний.

Главный же недостаток таких моделей - их громоздкость и трудоемкость. Огромное число реализаций, необходимое для нахождения искомых параметров с приемлемой точностью, требует большого расхода машинного времени. Кроме этого, результаты такого моделирования труднее осмыслить, чем расчеты аналитическими методами и, соответственно, труднее оптимизировать решение (в основном, наощупь). Наиболее целесообразным является сочетание аналитических и имитационных методов. Как правило, аналитическими методами рассчитываются отдельные элементы и блоки сложной системы, а затем, как из "кирпичиков", строится большая сложная имитационная модель.

Основным элементом, из совокупности которых складывается статистическая модель, является одна случайная реализация моделируемого явления.

Реализация - это как бы один экземпляр случайного явления со всеми присущими ему случайностями. Этим реализации отличаются одна от другой. Отдельная реализация разыгрывается с помощью специально разработанной процедуры (алгоритма), в которой основную роль играет "жребий" или, как говорят, "бросание жребия". Каждый раз, когда в ход явления вмешивается случай, его влияние учитывается не расчетом, а жребием.

Понятие "жребия". Пусть в ходе процесса наступил момент, когда его дальнейшее развитие (а значит и результат) зависит от того, произошло или нет какое-то событие А.

Тогда нужно "бросанием жребия" решить вопрос: произошло событие или нет? Как можно осуществить этот жребий? Необходимо привести в действие какой-либо механизм случайного выбора.

Если жребий бросается для того, чтобы узнать, произошло ли событие А, его нужно организовать так, чтобы условный результат розыгрыша имел ту же вероятность, что и событие А.

Кроме случайных событий на ход и исход операции могут влиять различные случайные величины.

С помощью жребия можно разыграть как значение любой случайной величины, так и совокупности значений нескольких величин.

Условимся называть "единичным жребием" любой опыт со случайным исходом, который отвечает на один из следующих вопросов:

1. Произошло или нет событие А?

2. Какое из событий А1, А2, ..., Аk произошло?

3. Какое значение приняла случайная величина Х?

4. Какую совокупность значений приняла система случайных величин Х1, Х2, ..., Хk?

Любая реализация случайного явления методом Монте-Карло строится из цепочки единичных жребиев, перемежающихся с обычными расчетами. Ими учитывается влияние исхода жребия на дальнейший ход событий (в частности на условия, в которых будет разыгран следующий жребий).

Единичный жребий может быть разыгран разными способами, но есть один стандартный механизм, с помощью которого можно осуществить любую разновидность жребия. А именно, для каждой из них достаточно уметь получать случайное число R, все значения которого от 0 до 1 равновероятны (т.е. обладают одинаковой плотностью вероятности).

Условно назовем величиной R "случайное число от 0 до 1". С помощью такого числа можно разыграть любой из четырех видов единичного жребия.

1. Основные понятия теории массового обслуживания.

2. Постановка задачи теории очередей.

3. Подходы решения задач теории очередей.

Практическая деятельность человека тесно связана с различного рода системами массового обслуживания. В области экономики - это банковское обслуживание, пользование объектами торговли и услугами сферы обслуживания и многие другие виды экономической деятельности.

Любая система массового обслуживания может включать в себя следующие элементы:

Входящий поток требований или заявок на обслуживание. Этот элемент является основным. Изучение входящего потока требований и его описание необходимо при организации любой системы массового обслуживания.

Очередь. В тех случаях, когда поступающие в систему массового обслуживания требования не могут быть удовлетворены немедленно, возникает очередь. В такой ситуации интерес может представлять длина этой очереди, порядок, по которому ожидающие требования направляются на обслуживание (как говорят, дисциплина очереди), время ожидания.

В отдельных случаях систем массового обслуживания очереди не допускаются, т.е. требование, заставшее систему занятой, не обслуживается (получает отказ).

Обслуживающее устройство. Этот элемент присутствует в любой системе массового обслуживания. От характеристик и параметров, способов организации обслуживающего устройства зависят не только время, необходимое на обслуживание одного требования, но и длина очереди и время ожидания.

Выходящий поток обслуженных требований. Этот элемент может оказаться очень важным в тех случаях, когда выходящий поток обслуженных требований является входящим для другой системы массового обслуживания.

Как правило, число требований на входе системы массового обслуживания за какой-либо промежуток времени и время обслуживания одного требования являются случайными величинами. Функционирование системы массового обслуживания в таком случае представляет собой случайный процесс, и методы исследования таких систем используют имитационное моделирование. Однако понять сущность задач и методов теории массового обслуживания можно на примерах детерминированных моделей систем массового обслуживания и прежде всего моделей теории очередей.

Основными компонентами модели очереди являются:

·  описание входящего потока требований;

·  описание способа, которым выполняется обслуживание (т.е. описание дисциплины обслуживания);

·  описание дисциплины очереди (т.е. каким образом из очереди выбираются клиенты на обслуживание: “первый пришел - первый обслужен”, “последний пришел - первый обслужен”, “по указанным приоритетам” и т.п.).

При конструировании модели очереди первоочередной задачей является символическое представление основных компонент, после чего изучаются соотношения между ними.

Принципиальными характеристиками очереди являются:

·  длина очереди в различные моменты времени;

·  общая продолжительность нахождения требования в системе обслуживания (т.е. время, потраченное на ожидание в очереди, плюс собственное время обслуживания);

·  время, в течение которого обслуживающее устройство было свободно.

Основной целью исследования систем массового обслуживания является установление равновесия между допустимыми нагрузками обслуживающего устройства, ограниченной пропускной способностью системы и раздражением клиента, с одной стороны, и допустимой стоимостью обслуживающих точек, с другой.

Рассмотрим систему массового обслуживания, имеющую один источник требований, проходящих через единственное обслуживающее устройство. Пусть имеют место следующие предположения:

Похожие работы

Курс отечественной политэкономии середины XIX-начала XX в. о методе экономического исследования

Скачать

23821

0

0

... именно в популярных курсах политической экономии. Отметим, однако, что интерес к вопросам методологии науки после Бутовского затихает вплоть до 90-х годов XIX в. Новый виток в развитии представлений о методе экономического исследования и интереса к этой теме в курсах политической экономии, пожалуй, начинается с "Оснований политической экономии" Д. Пихно, увидевших свет в 1890 г. Автор уже ...

Традиционные методы экономической статистики

Скачать

50665

0

0

... индекс физического оборота определяется отношением индекса оборота в действующих ценах и индекса цен, исчисляемый по схеме среднего гармонического индекса     2.                  Классические методы экономического анализа   a. Балансовый метод Этот метод применяется при изучении соотношения двух групп взаимосвязанных показателей, итоги которых должны быть равны между собой. Своим названием ...

Генетический метод в экономическом исследовании

Скачать

51117

0

1

... исследований дополняет и углубляет исторический метод, сближает его с методами естественных наук, способствует экстраполяции его на будущее хозяйственных феноменов.   Глава 2. Генетический метод в экономических исследованиях Эволюционный и исторический методы иногда можно представить как два вида генетического метода — метода исследования социальных явлений, основанного на анализе их ...

Предмет и методы экономической теории

Скачать

51177

0

0

... стоимости как об основном законе. Практика развития мировой цивилизации не подтвердила воплощение этих целей и привела к обратным (отрицательным) результатам. Из общего анализа предмета экономической теории, увеличения производства при ограниченных ресурсах формируются цели по удовлетворению потребностей и социализации общественно-экономической жизни. Это: • стабильный рост поступательного ...