Навигация
1. ЛММР
Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар у относительно отечественного производства х1, изменения запасов х2 и потребления на внутреннем рынке х3 оказалась следующей
![]()
при этом среднее значение для рассматриваемых признаков составили
![]()
на основе данной информации могут быть найдены средние значения по совокупности показатели эластичности
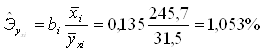
т.е. с ростом величины отечественного производства на 1% размер импорта в среднем по совокупности регионов возрастет на 1,053% при неизменных запасах и потребления семей.
2. РМ с переменной структурой (фиктивные переменные)
Проанализируем зависимость цен двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: "хрущевка", панельный кирпичный.
При использовании трех категорий домов вводятся две фиктивные переменные: z1 и z2.
Пусть переменная z1 принимает значение 1 для панельного дома и 0 для всех типов домов; переменная z2 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные z1 и z2 принимают значение 0 для домов типа "хрущевки".
![]()
![]()
"хрущевки" ![]() =320+500*х
=320+500*х
панельные ![]() =2520+500*х
=2520+500*х
кирпичные ![]() =1920+500*х
=1920+500*х
В рассматриваемом примере за базу сравнения цены взяты дома "хрущевки" для которых z1= z2=0
Параметр при z1=2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 дол. выше чем в "хрущевках". Соответственно параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600дол. при неизменной величине полезной площади по сравнению указанным типам домов.
3. Нелинейные РМ
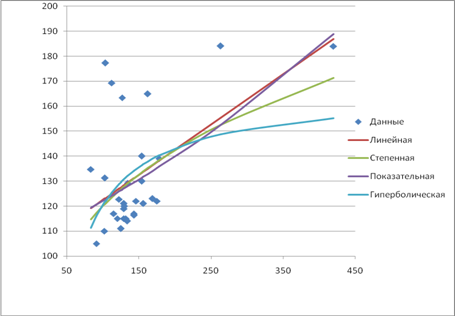
Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:
y=а*хb*![]()
y - спрашиваемое количество,
xb - цена,
![]() - случайная ошибка.
- случайная ошибка.
4. Модели временных рядов
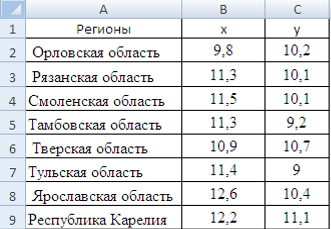
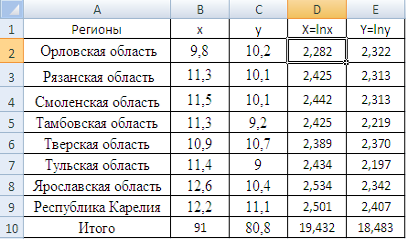
Имеются следующие данные о величине дохода на одного члена семьи и расходы на товар А.
| Показатель | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
| Расходы на товар А, руб. | 30 | 35 | 39 | 44 | 50 | 53 |
| Доход на одного члена семьи, % к 1985г. | 100 | 103 | 105 | 104 | 115 | 118 |
Ежегодные абсолютные приросты определяем по формулам
![]()
![]()
![]()
Расчеты можно представить в виде таблицы
| yt |
| xt |
|
| 30 | - | 100 | - |
| 35 | 5 | 103 | 3 |
| 39 | 4 | 105 | 2 |
| 44 | 5 | 104 | 4 |
| 50 | 6 | 115 | 6 |
| 53 | 3 | 118 | 5 |
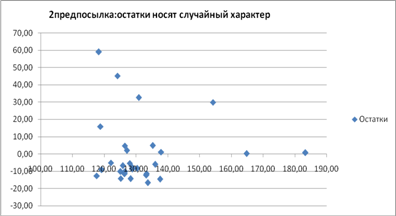
Значение у не имеют четко выраженной тенденции они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда, аналогичный вывод можно сделать и по ряду х.
Системы линейных одновременных уравнений
Модель вида

y - валовый национальный доход
y-1 - валовый национальный доход предшествующего года,
С - личное потребление,
D - конечный спрос (помимо личного потребления)
Информация за 9 лет о приросте всех показателей дана в таблице.
| Год | D | y-1 | У | С |
| 1 | -6,8 | 46,7 | 3,1 | 7,4 |
| 2 | 22,4 | 3,1 | 22,8 | 30,4 |
| 3 | -17,3 | 22,8 | 7,8 | 1,3 |
| 4 | 12,0 | 7,8 | 21,4 | 8,7 |
| 5 | 5,9 | 21,4 | 17,8 | 25,8 |
| 6 | 44,7 | 17,8 | 37,2 | 8,6 |
| 7 | 23,1 | 37,2 | 35,7 | 30 |
| 8 | 51,2 | 35,7 | 46,6 | 31,4 |
| 9 | 32,3 | 46,6 | 56,0 | 39,1 |
| ИТОГО | 167,5 | 239,1 | 248,4 | 182,7 |
Для данной модели была получена система приведенных уравнений

Похожие работы
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
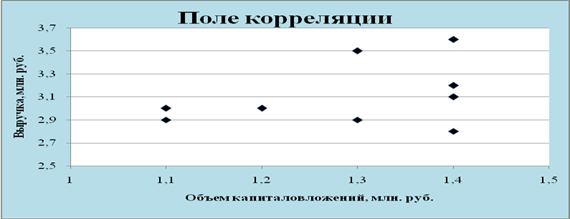
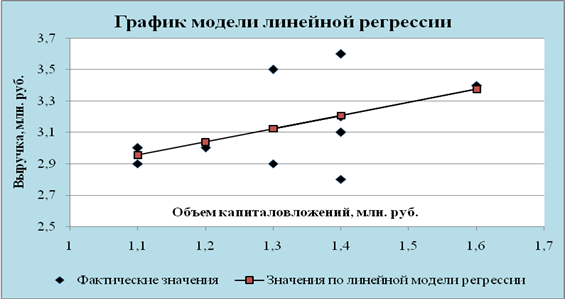
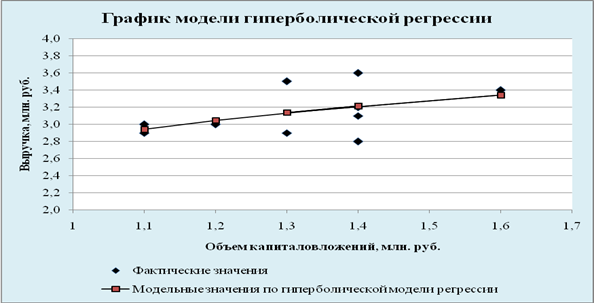
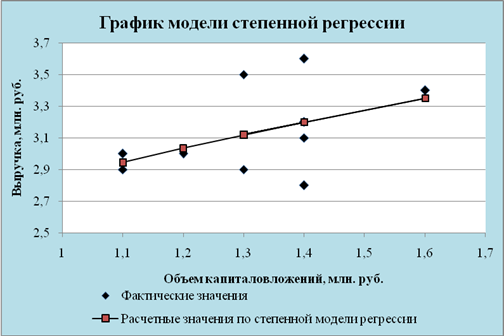
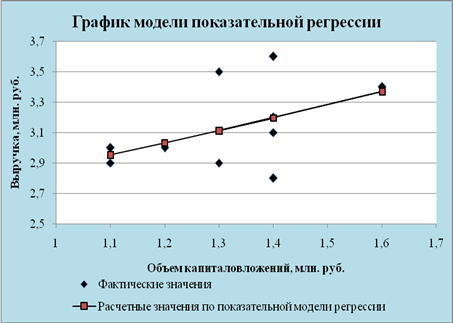
... . Но большее значение индекса корреляции, коэффициента детерминации, F – критерия Фишера и меньшее значение средней относительной ошибки аппроксимации имеет линейная модель. Т.е. она лучше и точнее из всех построенных моделей описывает зависимость выручки от объема капиталовложений. Ее можно взять в качестве лучшей для построения прогноза. 11. СДЕЛАЕМ ПРОГНОЗ НА СЛЕДУЮЩИЕ ДВА ГОДА показателя у ...
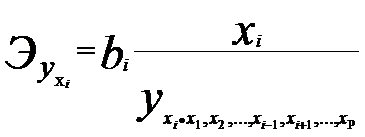
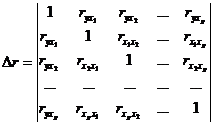
0 комментариев