Построение математических моделей

Содержание

Задание 1

Задание 2

Список литературы

Вариант 6

Задание 1

Имеются данные, характеризующие выручку (у, млн. руб.) предприятия «АВС» в зависимости от капиталовложений (х, млн. руб.) за последние 10 лет (табл. 1).

Таблица 1

Время, t	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007
Выручка, у	3,0	2,9	3,0	3,1	3,2	2,8	2,9	3,4	3,5	3,6
Объем капитало- вложений, х	1,1	1,1	1,2	1,4	1,4	1,4	1,3	1,6	1,3	1,4

1.  Построить поле корреляции.

2.  Найти параметры уравнения линейной регрессии ; дать экономическую интерпретацию параметров а и b.

3.  Составить уравнения нелинейных регрессий:

·  гиперболической ;

·  степной ;

·  показательной

4.  Для каждой из моделей:

-  найти коэффициент парной корреляции (для нелинейных регрессий – индекс корреляции);

-  найти коэффициент детерминации;

-  проверить значимость уравнения регрессии в целом с помощью F – критерия Фишера;

-  найти среднюю относительную ошибку аппроксимации.

5.  Составить сводную таблицу вычислений; выбрать лучшую модель; дать интерпретацию рассчитанных характеристик.

6.  По лучшей модели составить прогноз на следующие два года показателя у (выручка), если х (объем капиталовложений) увеличивается на 10% по сравнению с последним годом.

7.  Построить графики уравнений регрессии; отметить точки прогноза.

РЕШЕНИЕ:

1.  ПОСТРОИМ ПОЛЕ КОРРЕЛЯЦИИ

Поле корреляции – точечный график, осями X и Y которого сопоставлены изучаемые признаки (рис. 1).

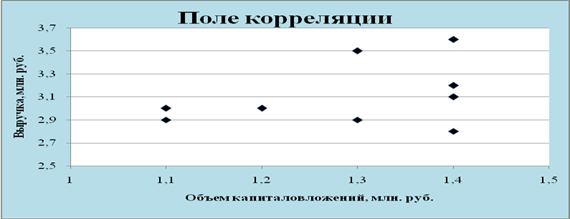
Рис. 1

Точки на графике поля корреляции находятся довольно хаотично, что говорит о слабой зависимости объема капиталовложений Х и выручки Y.

2.  НАЙДЕМ ПАРАМЕТРЫ ЛИНЕЙНОЙ РЕГРЕССИИ

Расчет неизвестных параметров выполним методом наименьших квадратов (МНК), построив систему нормальных уравнений и решая ее, относительно неизвестных параметров а и b.

Система нормальных уравнений имеет вид:

Необходимые расчеты представлены в таблице 2.

 

Построена линейная модель зависимости выручки предприятия «АВС» от объема капиталовложений:

В линейном регрессии коэффициент регрессии показывает направление связи между переменной Y и фактором X. А также, указывает насколько в среднем изменяется значение результативного признака Y, если фактор увеличить на единицу измерения.

b = 0,843, т.е. при увеличении объема капиталовложений (Х) на 1 млн. руб. выручка предприятия (Y) в среднем увеличится на 0,843 млн. руб.

Таблица 2

Вспомогательные вычисления для нахождения параметров линейной модели

t	Y	X	X2	X*Y
1998	3,0	1,1	1,21	3,3
1999	2,9	1,1	1,21	3,19
2000	3,0	1,2	1,44	3,6
2001	3,1	1,4	1,96	4,34
2002	3,2	1,4	1,96	4,48
2003	2,8	1,4	1,96	3,92
2004	2,9	1,3	1,69	3,77
2005	3,4	1,6	2,56	5,44
2006	3,5	1,3	1,69	4,55
2007	3,6	1,4	1,96	5,04
Σ	31,4	13,2	17,64	41,63

3.  РАССЧИТАЕМ:

-  коэффициент парной корреляции.

Коэффициент парной корреляции показывает направление и тесноту линейной связи.

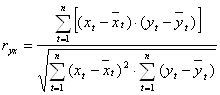
Т. е. связь между объемом капиталовложений и выручкой предприятия прямая и слабая.

Таблица 3

Вспомогательная таблица для расчета коэффициента парной корреляции, средней относительной ошибки аппроксимации

t	Y	X					A
1998	3,0	1,1	0,048	0,020	0,031	2,955	0,015
1999	2,9	1,1	0,048	0,058	0,053	2,955	0,019
2000	3,0	1,2	0,014	0,020	0,017	3,039	0,013
2001	3,1	1,4	0,006	0,002	-0,003	3,207	0,035
2002	3,2	1,4	0,006	0,004	0,005	3,207	0,002
2003	2,8	1,4	0,006	0,116	-0,027	3,207	0,146
2004	2,9	1,3	0,000	0,058	0,005	3,123	0,077
2005	3,4	1,6	0,078	0,068	0,073	3,376	0,007
2006	3,5	1,3	0,000	0,130	-0,007	3,123	0,108
2007	3,6	1,4	0,006	0,212	0,037	3,207	0,109
Σ	31,4	13,2	0,216	0,684	0,182		0,530

коэффициент детерминации

Коэффициент детерминации показывает долю вариации результативного признака Y под влиянием фактора Х, включенного в модель.

22,42% изменения выручки предприятия обусловлено изменением объема капиталовложений, на 77,58% влиянием прочих факторов, не учтенных в модели.

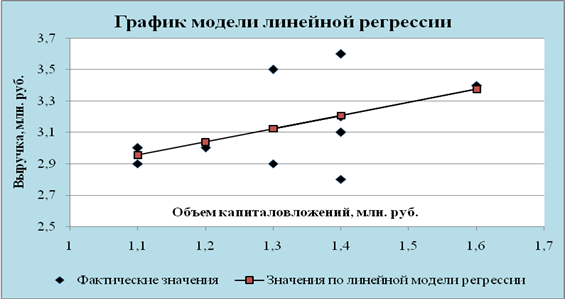
Рис. 2

F – критерий Фишера

Для проверки значимости уравнения регрессии в целом найдем расчетное значение критерия Фишера:

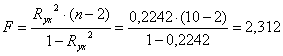
Расчетное значение статистики Фишера сравниваем с табличным

F(α; d.f.₁; d.f.₂), где

α – уровень значимости (для большей надежности примем его равным 0,05);

Число степеней свободы d.f.₁ = k = 1, где k – число факторов в модели;

Число степеней свободы d.f.₂ = n – k – 1 = 10 – 1 – 1 = 8

F (0.05; 1; 8) = 5,318.

В силу того, что F(расч.) = 2,312 < F(табл.)= 5,318, то уравнение в целом можно считать статистически незначимым.

Среднюю относительную ошибку аппроксимации:

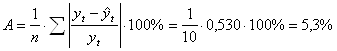
Фактические значения выручки отличаются от расчетных, полученных по модели на 5,3%. Ошибка небольшая, модель считается точной

4.  НАЙДЕМ ПАРАМЕТРЫ ГИПЕРБОЛИЧЕСКОЙ МОДЕЛИ РЕГРЕССИИ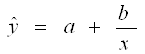

Расчет неизвестных параметров выполним методом наименьших квадратов (МНК).

Система нормальных уравнений имеет вид:

Необходимые расчеты представлены в таблице 4.

Таблица 4

Вспомогательная таблица для расчетов показателей по гиперболической модели

t	Y	X	1/Х	1/Х^2	Y/X			A
1998	3,0	1,1	0,909	0,826	2,727	2,940	0,004	0,020
1999	2,9	1,1	0,909	0,826	2,636	2,940	0,002	0,014
2000	3,0	1,2	0,833	0,694	2,500	3,047	0,002	0,016
2001	3,1	1,4	0,714	0,510	2,214	3,215	0,013	0,037
2002	3,2	1,4	0,714	0,510	2,286	3,215	0,000	0,005
2003	2,8	1,4	0,714	0,510	2,000	3,215	0,172	0,148
2004	2,9	1,3	0,769	0,592	2,231	3,137	0,056	0,082
2005	3,4	1,6	0,625	0,391	2,125	3,341	0,004	0,017
2006	3,5	1,3	0,769	0,592	2,692	3,137	0,132	0,104
2007	3,6	1,4	0,714	0,510	2,571	3,215	0,148	0,107
Σ	31,4	13,2	7,672	5,962	23,983		0,533	0,549

Построена гиперболическая модель зависимости выручки предприятия «АВС» от объема капиталовложений:

5.  РАССЧИТАЕМ:

-  индекс корреляции:

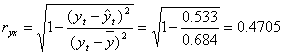
Связь между объемом капиталовложений и выручкой предприятия в гиперболической модели слабая

-  коэффициент детерминации

22,13% изменения выручки предприятия в гиперболической модели происходит под влиянием изменением объема капиталовложений и на 77,87% под влиянием факторов, не включенных в модель.

-  F – критерий Фишера

Проверим значимость уравнения

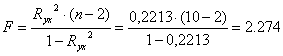
F(расч.) = 2,274< F(табл.)= 5,318, т.е. уравнение в целом можно считать статистически незначимым.

Среднюю относительную ошибку аппроксимации:

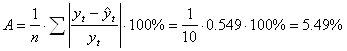
Ошибка меньше 7%, модель можно считать точной.

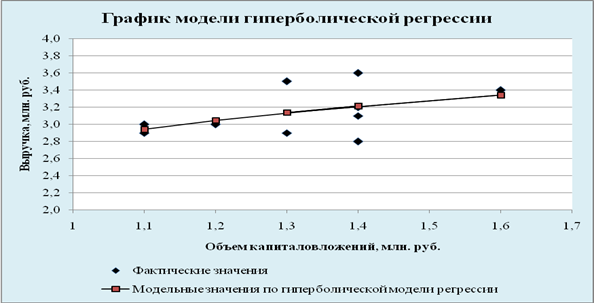
Рис. 3