Внести коэффициенты при неизвестных в уравнениях и целевой функции в верхние ячейки клеток табл.1.3 (исходный план)

3. Внести коэффициенты при неизвестных в уравнениях и целевой функции в верхние ячейки клеток табл.1.3 (исходный план).

4. Выбрать генеральный элемент. Для этого:

·  найти в верхней строке симплекс-таблицы максимальный положительный элемент (4,04). Если в верхней строке симплекс-таблицы нет положительных элементов, то записанное в данной симплекс-таблице базисное решение будет оптимальным, т.е. уменьшить значение целевой функции при переходе от одного допустимого базисного решения к другому не представляется возможным;

·  составить отношение свободных членов (первый столбец табл.1.3) к положительным коэффициентам выбранного столбца. В задаче: 23,60/1,20=19,67; 18,92/1,00=18,92; 12,08/0,92=13,13;

·  выбрать среди найденных отношений наименьшее (13,13). Если наименьшее отношение достигается при нескольких значениях, то можно выбрать любое. Элемент выбранного столбца, которому соответствует наименьшее отношение, - генеральный элемент (в табл.1.3 клетка выделена жирной линией).

5. Найти значение, обратное генеральному элементу, внести его в правый угол клетки, содержащей генеральный элемент (1/0,92=1,09).

6. Все коэффициенты из верхних отделений строки, где расположен генеральный элемент, умножить на значение, обратное генеральному элементу, и поместить полученные произведения в соответствующие правые углы клеток той же строки (12,08´1,09=13,13; 0,62´1,09=0,67 и т.д.).

7. Умножить на значение, обратное генеральному элементу, со знаком «-» все коэффициенты (кроме генерального элемента) из левых углов клеток столбца, где расположен генеральный элемент, и поместить полученные произведения в соответствующие правые углы клеток этого же столбца (4,04´1,09= -4,39; 1,20´1,09= -1,30 и т.д.).

8. Выделить числа, находящиеся в левых углах клеток строки, где расположен генеральный элемент, и в правых углах клеток столбца, в котором содержится генеральный элемент.

9. Заполнить оставшиеся правые углы клеток числами, полученными перемножением соответствующих выделенных чисел (-4,39´12,08= -53,03; -4,39´0,62= -2,72;.....-1,30´12,08= -15,70 и т.д.).

10. Перейти к новому набору свободных неизвестных. Для этого:

ü  из правых углов клеток строки и столбца, на пересечении которых находится генеральный элемент, перенести все числа в левые углы соответствующей строки и столбца последующей таблицы (первая итерация - табл.1.4);

ü  в левые углы остальных клеток последующей таблицы записать числа, равные алгебраической сумме чисел из левого и правого углов соответствующей клетки предыдущей таблицы (-53,03+205,20=152,17; -2,72+1,91= -0,81;...…. –15,70+23,60=7,90 и т.д.);

ü  поменять местами переменные на пересечении строки и столбца, где расположен генеральный элемент ( х₅ и х₁₀).

11. Если в верхней строке новой таблицы все коэффициенты при свободных неизвестных отрицательны, то полученный результат является оптимальным, план не подлежит улучшению, а целевая функция принимает свое наименьшее значение. В противном случае решение задачи следует продолжить для чего необходимо вновь перейти к п.4.

При решении задачи оптимальный план формирования пассажирских поездов был получен после второй итерации (табл.1.6). Он предусматривает следующие назначения:

Ø  А-Г (х₂) - 8 поездов;

Ø  А-В (х₃) - 1 поезд;

Ø  А-Б (х₄) - 9 поездов;

Ø  Б-Д (х₅) - 13 поездов.

Таблица 1.3

Базисное решение

			-x1		-x2		-x3		-x5		-x6		-x8
F	205,2		1,91		2,12		1,29		4,04		2,10		1,32
	-53,03		-2,72		0		0			-4,39	0		-4,39
x4	15,00		0,62		0,69		0,77		0		0		0
	0		0		0		0			0	0		0
x7	23,60		0,80		0,90		1,00		1,20		1,10		0
	-15,70		-0,81		0		0			-1,30	0		-1,30
x9	18,92		0,67		0,75		0		1,00		0,92		1,08
	-13,18		-0,68		0		0			-1,09	0		-1,09
x10	12,08		0,62		0		0		0,92		0		1,00
	13,13		0,67		0		0		1,09		0		1,09

 

Таблица 1.4

Первая итерация

			-x1		-x2			-x3		-x10		-x6		-x8
F	152,17		-0,81		2,12			1,29		-4,39		2,10		3,07
	-16,47		0,03			-2,87		0		3,13		2,64		0,03
x4	15,00		0,62		0,69			0,77		0		0		0
	-5,28		0,01			-0,92		0		1,00		-0,85		0,01
x7	7,90		0,80		0,90			1,00		-1,30		1,10		-1,30
	-6,89		0,01			1,20		0		1,30		-1,10		0,01
x9	5,74		-0,01		0,75			0		-1,09		0,92		-0,01
	7,65		-0,01		1,33			0		-1,45		1,23		-0,01
x5	13,13		0,67		0			0		1,09		0		1,09
	0		0				0	0		0		0		0

Таблица 1.5

Вторая итерация

			-x1		-x9		-x3			-x10		-x6		-x8
F	135,70		-0,78		-2,87		1,29			-1,26		-0,54		-3,04
	-1,30		-1,04		1,55			-1,29		0		0		1,66
x4	9,72		0,63		-0,92		0,77			1,00		-0,85		0,01
	-0,78		-0,63		0,92			-0,77		0		0		0,99
x7	1,01		0,81		-1,25		1,00			0		0		-1,29
	1,01		0,81		-1,27		1,00			0		0		-1,29
x2	7,65		-0,01		1,33		0			-1,45		1,23		-0,01
	0		0		0				0	0		0		0
x5	13,13		0,67		0		0			1,09		0		1,09
	0		0		0				0	0		0		0

При этом целевая функция уменьшится на 70,8 и составит 134,4 стоимостных единицы.

Таблица 14

Оптимальный план формирования пассажирских поездов

		-x1	-x9	-x7	-x10	-x6	-x8
F	134,40	-1,82	-1,32	-1,29	-1,26	-0,54	-1,38
x4	8,94	0	0	-0,77	1,00	0,85	1,00
x3	1,01	0,81	-1,20	1,00	0	0	-1,29
x2	7,65	-0,01	1,33	0	1,45	1,23	-0,01
x5	13,13	0,67	0	0	1,09	0	1,09

Дробную часть результирующего числа пассажирских поездов следует округлять по правилу:

·  до 0,2 - отбросить;

·  от 0,2 до 0,7 - округлить до 0,5 и предусмотреть назначение дополнительного пассажирского поезда с режимом движения «через день»;

·  более 0,7 - округлить до 1.

На заключительной стадии следует проверить выполнение неравенств (1.2). Если они соблюдаются, то задача решена верно.

Анализ полученных результатов показывает отсутствие прямых поездов назначением А-Д. Следовательно, пассажиры, следующие из А до Д будут вынуждены делать пересадку на одной из попутных станций: Б, В или Г. Пассажиры других маршрутов перемещаются в беспересадочном сообщении.

1.3.Определение потребного числа составов поездов и парка пассажирских вагонов

После расчета оптимального плана формирования пассажирских поездов необходимо перейти к определению потребного их числа для каждого назначения и в целом для рассматриваемого полигона.

Нахождение потребного числа составов может производиться графическим или аналитическим путем.

В первом случае производится построение графика следования пассажирских поездов (отдельно каждого назначения) и их оборота на головной и конечной станциях. При этом, период, на который строится график, принимается не менее длительности оборота одного состава. Затем по графику подсчитывается потребное число составов «в обороте».

В курсовом проекте следует отдать предпочтение аналитическому методу. В этом случае потребное число составов пассажирских поездов каждого назначения может быть рассчитано по формуле (с округлением до целого большего):

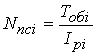,  (1.7)

где  - потребное число составов пассажирских поездов -го назначения;

 - продолжительность оборота пассажирского поезда -го назначения;

 - расчетный интервал отправления пассажирских поездов -го назначения с головной станции, равный:

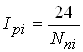,  (1.8)

где  - число пассажирских поездов -го назначения, рассчитанное в соответствии с оптимальным планом их формирования.

Продолжительность оборота состава пассажирского поезда:

, (1.9)

где  - минимальное время нахождения пассажирского состава соответственно на головной станции и на станции его оборота, ч;

 - время хода пассажирского поезда -го назначения соответственно в четном и нечетном направлениях,ч;

- суммарное время стоянок пассажирского поезда -го назначения на попутных станциях за один оборот (при следовании его в четном и нечетном направлениях), ч;

 - количество попутных станций, на которых пассажирский поезд -го назначения имеет остановки за полное время его оборота;

  - время на разгон и замедление пассажирского поезда, ч.

Так, например, если принять время хода пассажирских поездов по участкам: Б-В – 4 ч, В-Г – 4.5 ч, А-Б: в четном направлении – 3,4 ч, а в нечетном – 3,6 ч; время на разгон и замедление – по 1 мин (в сумме – 0,03 ч); продолжительность стоянки пассажирского поезда на попутной станции 12 мин (0,2 ч); время нахождения состава «по обороту» на станции А – 6 ч и на станции Г – 4 ч, то суммарное время оборота состава пассажирского поезда, следующего назначением А-Г:

 ч.

Расчетный интервал следования поездов данного назначения:

 ч.

Тогда потребное число составов пассажирских поездов, следующих назначением А-Г:

 составов.

В дальнейшем, зная композицию каждого состава и их количество определяется потребность в парке пассажирских вагонов: купейных, плацкартных и др.:

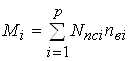,  (1.10)

где - число назначений пассажирских поездов в оптимальном плане их формирования;

  - рассчитанное число пассажирских составов -го назначения «в обороте»;

 - количество вагонов данного типа в составах поездов -го назначения.

1.4.Расчет показателей пассажирских перевозок в дальнем и местном сообщениях

Для оценки объема выполненной работы и качества использования подвижного состава применяется система количественных и качественных показателей по дальнему и местному пассажирскому движению.

К количественным показателям относятся:

1). Количество отправленных пассажиров:

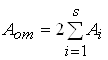,  (1.11)

где - число струй пассажиропотоков (в курсовом проекте );

 - величина -й струи пассажиропотока.

2). Пассажирооборот (пасс-км):

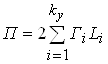, (1.12)

где  - количество участков на рассматриваемом полигоне (в курсовом проекте );

 - густота движения пассажиров на -м участке полигона, чел.;

 - протяженность -го участка, км.

3). Пробег поездов (поездо-км):

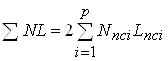,  (1.13)

где  - расстояние пробега пассажирского поезда -го назначения (расстояние между головной и станцией оборота пассажирского поезда -го назначения), км.

4). Пробег вагонов (вагоно-км):

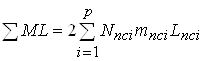, (1.14)

где  - число вагонов в составах пассажирских поездов -го назначения.

5). Вагоно-осе-км:

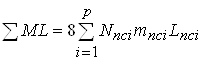. (1.15)

6). Средняя дальность поездки пассажиров (км):

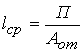. (1.16)

7). Средний состав пассажирского поезда в вагонах:

(1.17)

и в осях:

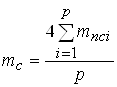. (1.18)

Качественные показатели пассажирских перевозок определяются по формулам:

1). Среднее время оборота составов (ч):

. (1.19)

Здесь  рассчитывается по формуле (1.9) для каждого назначения пассажирских поездов в оптимальном плане их формирования.

2). Среднесуточный пробег состава пассажирского поезда (км):

.  (1.20)

3). Средняя населенность (пассаж.) состава:

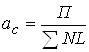;  (1.21)

вагона:

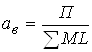. (1.22)

4). Коэффициент использования вместимости составов:

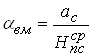, (1.23)

где  - средневзвешенное число посадочных мест в составах пассажирских поездов, рассчитываемое по формуле:

, (1.24)

где  - число посадочных мест в пассажирском поезде -го назначения, определяемое по формуле (1.1).

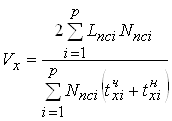
5). Ходовая скорость движения пассажирских поездов (км/ч):

. (1.25)

6). Техническая скорость движения пассажирских поездов (км/ч):

.  (1.26)

7) Участковая скорость движения пассажирских поездов (км/ч):

. (1.27)

В формулах (1.25)¸(1.27) обозначения слагаемых в знаменателе идентичны приведенным к формуле (1.1).