Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения

2.2 Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения

Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации  и эмпирическое корреляционное отношение Эмпирический коэффициент детерминации  оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель  рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле

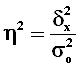, (9)

где  – общая дисперсия признака Y,

 – межгрупповая (факторная) дисперсия признака Y.

Значения показателя  изменяются в пределах . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство  =0, а при наличии функциональной связи между ними - равенство =1.

Общая дисперсия  характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле

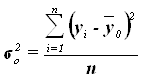 (10)

где y_i – индивидуальные значения результативного признака;

– общая средняя значений результативного признака;

n – число единиц совокупности.

Общая средняя  вычисляется как средняя арифметическая простая по всем единицам совокупности:

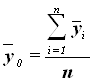 (11)

или как средняя взвешенная по частоте групп интервального ряда:

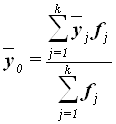 (12)

Для вычисления  удобно использовать формулу (11), т.к. в табл. 8 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.

Расчет  по формуле (11):

=133080/30=4436 млн руб.

Для расчета общей дисперсии  применяется вспомогательная таблица 12.

Таблица 12

Вспомогательная таблица для расчета общей дисперсии

Номер банка п/п	Собственный капитал, млн руб.
1	2	3	4	5
1	3900	-536	287296	15210000
2	4500	64	4096	20250000
3	3000	-1436	2062096	9000000
4	2300	-2136	4562496	5290000
5	3700	-736	541696	13690000
6	3200	-1236	1527696	10240000
7	3780	-656	430336	14288400
8	4000	-436	190096	16000000
9	3100	-1336	1784896	9610000
10	4600	164	26896	21160000
11	2200	-2236	4999696	4840000
12	5280	844	712336	27878400
13	4700	264	69696	22090000
14	4400	-36	1296	19360000
15	6500	2064	4260096	42250000
16	5000	564	318096	25000000
17	2500	-1936	3748096	6250000
18	1800	-2636	6948496	3240000
19	4200	-236	55696	17640000
20	5600	1164	1354896	31360000
21	7962	3526	12432676	63393444
22	5850	1414	1999396	34222500
23	400	-4036	16289296	160000
24	4900	464	215296	24010000
25	8400	3964	15713296	70560000
26	7088	2652	7033104	50239744
27	5100	664	440896	26010000
28	4300	-136	18496	18490000
29	6020	1584	2509056	36240400
30	4800	364	132496	23040000
Итого	133080	0	90670008	681012888

Расчет общей дисперсии по формуле (10):

=90670008/30=3022333,6

Общая дисперсия может быть также рассчитана по формуле

,

где  – средняя из квадратов значений результативного признака,

 – квадрат средней величины значений результативного признака.

Для демонстрационного примера

=681012888/30=22700429,6

=19678096

Тогда

=-=22700429,6-19678096=3022333,6

Межгрупповая дисперсия  измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних  от общей средней . Показатель  вычисляется по формуле

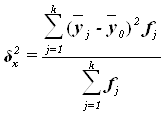, (13)

где  –групповые средние,

 – общая средняя,

–число единиц в j-ой группе,

k – число групп.

Для расчета межгрупповой дисперсии  строится вспомогательная таблица 13 При этом используются групповые средние значения  из табл. 8 (графа 5).

Таблица 13

Вспомогательная таблица для расчета межгрупповой дисперсии

Группы банков по прибыли, млн руб.	Число банков,	Среднее значение  в группе
1	2	3	4	5
50-110	3	2100	-2336	16370688
110-170	6	3080	-1356	11032416
170-230	12	4340	-96	110592
230-290	7	5694	1258	11077948
290-350	2	8181	3745	28050050
Итого	30			66641694

Расчет межгрупповой дисперсии  по формуле (11):

=66641694/30=2221389,8

Расчет эмпирического коэффициента детерминации  по формуле (9):

=2221389,8/3022333,6=0,735 или 73,5%

Вывод. 75,3% вариации суммы прибыли банков обусловлено вариацией объема прибыли, а 24,7% – влиянием прочих неучтенных факторов.

Эмпирическое корреляционное отношение  оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

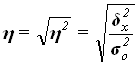 (14)

Значение показателя изменяются в пределах . Чем ближе значение  к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе  служит шкала Чэддока (табл. 14):

Таблица 14

Шкала Чэддока

	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика силы связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

Расчет эмпирического корреляционного отношения  по формуле (14):

=0,857 или 85,7 %

Вывод. Согласно шкале Чэддока связь между объемом прибыли и суммой собственного капитала банков является тесной.

ЗАДАНИЕ 3

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1. Ошибку выборки средней прибыли и границы, в которых будет находиться средний размер прибыли в генеральной совокупности.

2. Ошибку выборки доли банков с прибылью 230 и более млн. руб. и границы, в которых будет находиться генеральная доля.

Выполнение Задания 3

 

3.1 Определение ошибки выборки для средней прибыли банков и границ, в которых будет находиться средний размер прибыли в генеральной совокупности

Применение выборочного метода наблюдения всегда связано с установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки (ошибкой репрезентативности).

Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок - среднюю  и предельную .

Средняя ошибка выборки  - это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[].

Величина средней ошибки выборки рассчитывается дифференцированно (по различным формулам) в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка  выборочной средней  определяется по формуле

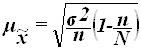 (15)

где  – общая дисперсия выборочных значений признаков,

N – число единиц в генеральной совокупности,

n – число единиц в выборочной совокупности.

Предельная ошибка выборки  определяет границы, в пределах которых будет находиться генеральная средняя:

,

, (16)

где – выборочная средняя,

 – генеральная средняя.

Границы задают доверительный интервал генеральной средней, т.е. случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют доверительной вероятностью или уровнем надёжности.

В экономических исследованиях чаще всего используются доверительные вероятности Р= 0.954, Р= 0.997, реже Р= 0,683.

В математической статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке µ с коэффициентом кратности t (называемым также коэффициентом доверия), который зависит от значения доверительной вероятности Р. Для предельной ошибки выборочной средней  это теоретическое положение выражается формулой

 (17)

Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р значения t задаются следующим образом (табл. 15):

Таблица 15

Доверительная вероятность P	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

По условию выборочная совокупность насчитывает 30 банков, выборка 5% механическая, следовательно, генеральная совокупность включает 600 банков. Выборочная средняя , дисперсия  определены в Задании 1. Значения параметров, необходимых для решения задачи, представлены в табл. 16:

Таблица 16

Р	t	n	N
0,683	1	30	600	198	3956

Расчет средней ошибки выборки по формуле (15):

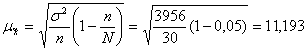млн руб.

Расчет предельной ошибки выборки по формуле (17):

млн руб.

Определение по формуле (16) доверительного интервала для генеральной средней:

Вывод. На основании проведенного выборочного обследования коммерческих банков региона с вероятностью 0,683 можно утверждать, что для генеральной совокупности банков средний объем прибыли находится в пределах от 186,807 млн руб. до 209,193 млн руб.