Навигация
Задача про розкрій
1.2.3 Задача про розкрій
Задача оптимального розкрою матеріалів полягає у визначенні найбільш раціонального способу розкрою наявного матеріалу (колоди, сталеві смуги, шкіра і т.д.), при якому буде виготовлено найбільшу кількість готових виробів у заданому асортименті чи буде досягнуто найменшу кількість відходів. Нехай на обробку поступає a одиниць сировинного матеріалу одного виду (наприклад, a колод однієї довжини). З нього потрібно виготовити комплекти, в кожен з яких входить n видів виробів у кількості, пропорційній числах. Є m способів розкрою (обробки) даного матеріалу, тобто відомі величини визначають кількість одиниць j-х виробів при i-му способі розкрою одиниці сировинного матеріалу [10].
Визначити план розкрою, що забезпечує максимальну кількість комплектів. Згідно з умовами завдання маємо таблицю розкрою:
Таблиця 3.
| Вид виробу Спосіб розкрою | 1 | ... | j | ... | n |
| 1 | a11 | ... | a1j | ... | a1n |
| … | ... | ... | ... | ... | ... |
| i | ai1 | ... | aij | ... | ain |
| … | ... | ... | ... | ... | ... |
| m | am1 | ... | amj | ... | amn |
Нехай ![]() – кількість одиниць сировинного матеріалу, розкроюється i-м варіантом (
– кількість одиниць сировинного матеріалу, розкроюється i-м варіантом (![]() .
.
Тоді кількість виробів 1-го виду одно:
![]() .
.
Беручи до уваги умову комплектності, маємо:
![]()
де y – кількість комплектів.
Аналогічні рівності можна записати і для всіх інших видів виробів, тобто умова комплектності призводить до системи обмежень:
![]()
Очевидно, що
![]()
(на розкрій надходить a одиниць сировинного матеріалу), а також
![]()
Мета задачі – максимізувати кількість комплектів:
![]() .
.
Отже, приходимо до математичної моделі задачі про розкроєння:
![]() ,
,
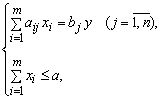
![]() .
.
Щоб виразити цільову функцію через змінні x1,…,xm, достатньо скористуватися будь-яким із співвідношень:
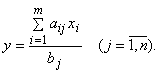
Похожие работы
... програмування та її економіко – математичної моделі, опис функцій і команд у вирішенні задач лінійного програмування засобами Exel, а також рішення конкретної задачі за допомогою ПК. 1. Побудова економіко–математичної моделі Загальна модель задачі математичного програмування має такий вигляд: У структурі моделі (1.1) можна виділити 3 елементи: 1) Набір керованих змінних x1, x2, ... x ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
2х1+5х2 + 15х3+ 10х4 досягає максимуму при системі обмежень: Розв'язуємо задачу лінійного програмування симплексним методом. Введемо балансні змінні х5 ≥ 0, х6≥ 0, х7≥ 0. Їх величина поки що невідома, але така, що перетворює відповідну нерівність у точну рівність. Після цього, задача лінійного програмування набуде вигляду: ∫ = 12х1+5х2 + 15х3+ 10х4 → max при ...
... – відпускна ціна i-го заводу j-й продукції; - закупівельна ціна i-го заводу j-й продукції, - шуканий обсяг закупівель на i-м заводі j-й продукції. 2.5 Перевірка моделі оптимізації на контрольному прикладі В цьому підрозділі на прикладі підприємства ТОВ "Гермес-Груп" розрахуємо модель (2.4.5) за допомогою електроних таблиць MSEcxel. Цільова функція має вигляд: де - об’єм закупівлі; ...


0 комментариев