Навигация
3. Синтез компенсатора
Для того, чтобы добиться желаемого качества процесса управления или регулирования (требуемой точности системы и качества переходного процесса), можно изменить структуру системы, введя дополнительные звенья корректирующие устройства (компенсаторы).
Основная задача компенсаторов состоит в улучшении точности системы и качества переходных процессов.
Систему с компенсатором можно представить в виде:
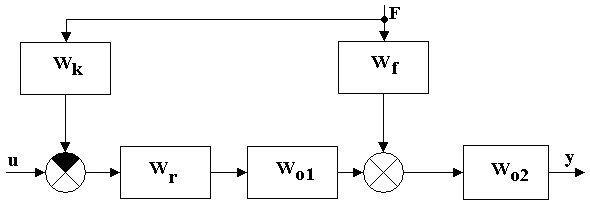
Рис. 8. Система с компенсатором
Рассчитать компенсатор можно следующим образом:
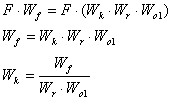
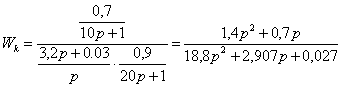
Условие физической реализуемости компенсатора соблюдено – степень числителя не превышает степень знаменателя.
Промоделируем в Simulink систему без учёта компенсатора
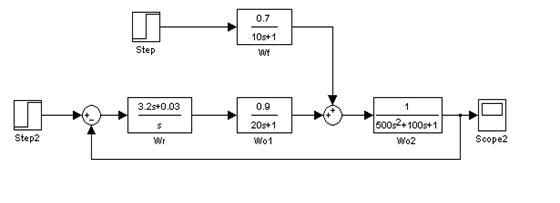
Рис. 9. Структура системы без компенсатора
Характеристика системы будет следующей
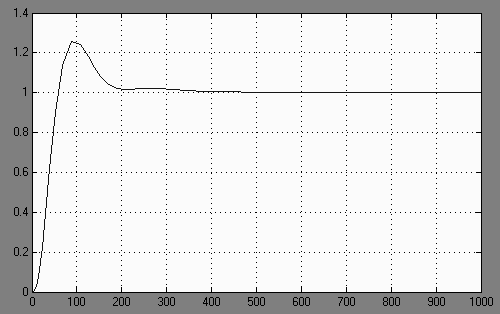
Рис. 10. Поведение системы без компенсатора
Промоделируем в Simulink систему с учётом компенсатора
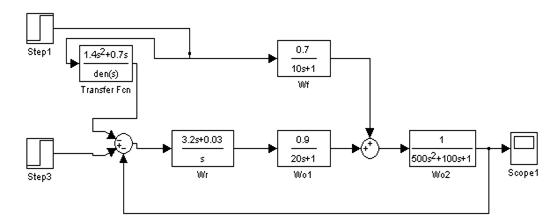
Рис. 11. Структура системы с компенсатором
Характеристика системы будет следующей
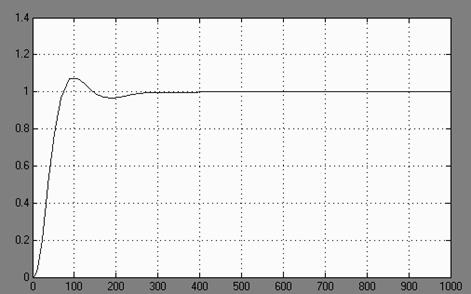
Рис. 12. Поведение системы с компенсатором
Характеристики систем
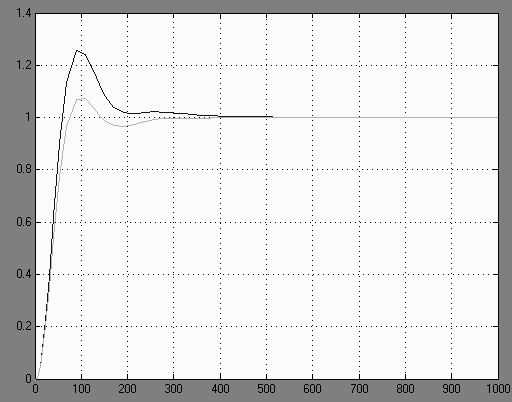
Рис. 13.
Из Рис. 13 делаем вывод : компенсатор снизил возникшую при введении в систему внешнего воздействия ошибку.
4. Синтез дискретного регулятора
Предполагается, что ступенчатое изменение задающей переменной происходит в момент времени k=0:
ω(k)=1 для k= 0,1,2,… .
Так как время запаздывания не равно нулю (d≠0), то необходимо использовать следующую модель объекта:
![]() (2.1)
(2.1)
Коэффициенты этой модели удовлетворяют соотношениям:
![]()
![]()
![]() (2.2)
(2.2)
![]()
На процесс управления наложены теперь следующие ограничения:
y(k)=ω(k)=1 для k ≥ ν=m+d,
u(k)=u(m) для k ≥ m.
Тогда параметры регулятора:
![]()
![]()
![]()
![]()
![]() (2.3)
(2.3)
![]()
![]()
![]()
Таким образом, получим передаточную функцию апериодического регулятора:
![]() (2.4)
(2.4)
Отсюда следует, что передаточная функция по задающему сигналу при использовании точной модели объекта будет равна:
![]() (2.5)
(2.5)
а ее характеристическое уравнение:
![]() (2.6)
(2.6)
что говорит об апериодическом характере переходного процесса.
Будем рассчитывать регулятор, включенный последовательно с объектом, с помощью Matlab’а.
| W1=tf([0.9],[20 1],'td', 1) % задаем передаточную функцию W2=tf([1],[500 100 1],'td', 15) % задаем передаточную функцию Wob=W1*W2 % общая передаточная двух последовательных частей системы T=1 % время квантования Wdiskr=c2d(Wob,T,'zoh') % передаточная в дискретной области [Numer Denom]=tfdata(Wdiskr, 'v') % коэффициенты числителя и знаменателя m=length (Numer) Denom1=Denom(2:m) Numer1=Numer(2:m) q0=1/sum(Numer1) for i=1:(m-1) q(i)=q0*Denom1(i) p(i)=q0*Numer1(i) end Q=[q0 q] % матрица коэффициентов числителя P=[1 -p] % матрица коэффициентов знаменателя Wr=tf(Q, P, T) % передаточная функция регулятора |
Получим значение передаточной функции дискретного регулятора:
![]()
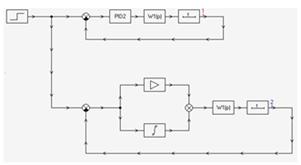
Посмотрим на поведение системы при использовании такого регулятора. Промоделируем поведение системы в Simulink’e.

Рис. 12. Структура системы с дискретным регулятором
Получим следующий график:
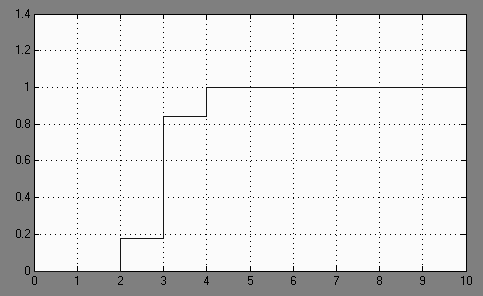
Рис. 13. Поведение системы с дискретным регулятором
Как видно из полученного графика, установившаяся ошибка и время перерегулирования отсутствует. Время регулирования составляет 3 такта.
Таким образом, произведен синтез дискретного регулятора.
Похожие работы
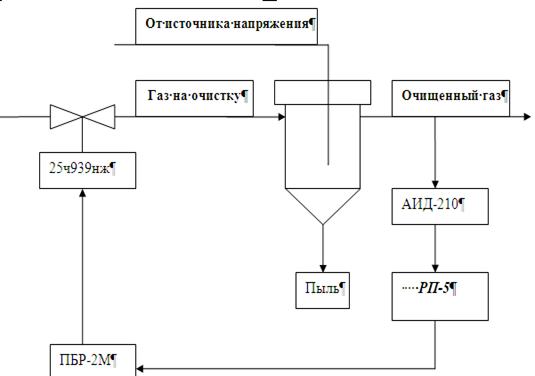
... параметры. Показателем эффективности данного процесса является степень очистки газа. Для решения задачи построена одноконтурная система управления процессом электрической очистки газа. Выбран регулятор и построена математическая модель системы управления. На модели определены оптимальные параметры регулятора. Выбраны приборы для основного контура регулирования. 1. Специальная часть ...
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
... устройства, которое нужно добавить к некоторой неизменяемой части системы, чтобы обеспечит требуемое качество системы в установившемся и переходном режимах. Наиболее приемлемым для решения задачи динамического синтеза является метод логарифмических амплитудных характеристик (метод ЛАХ). [1, § 12.5] Стадии синтеза по методу ЛАХ включают: 1. построение располагаемой ЛАХ, т.е. ЛАХ исходной ...
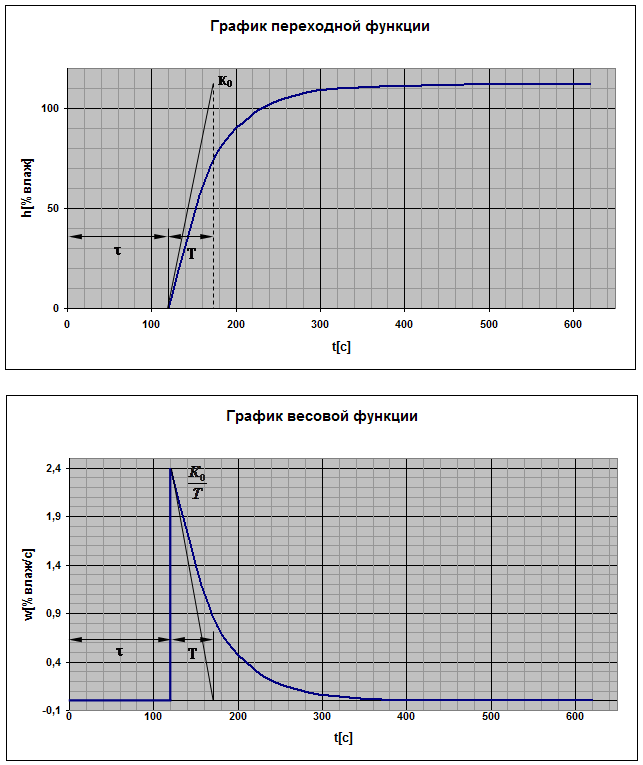
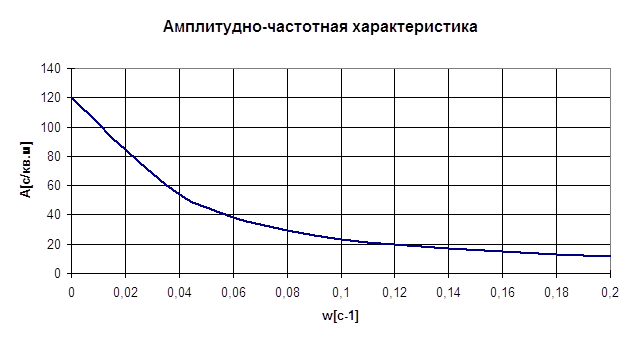
... воздействие) Δf(t) [%] - изменение концентрации массы (возмущающее воздействие) Δy(t) [г/м2] – изменение массы 1кв.м. полотна (выходная переменная) Временные характеристики по каналу управления. Передаточная функция объекта регулирования. Wоб(р) = К0 - коэффициент передачи - постоянная времени Т =50 с - запаздывание информации t =120 ...


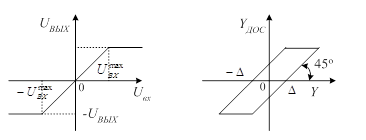


0 комментариев