Навигация
Синтез дискретного компенсатора
5. Синтез дискретного компенсатора
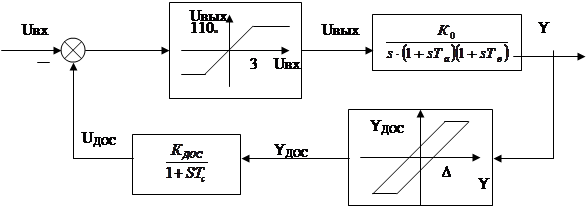
Систему с компенсатором можно представить в виде:
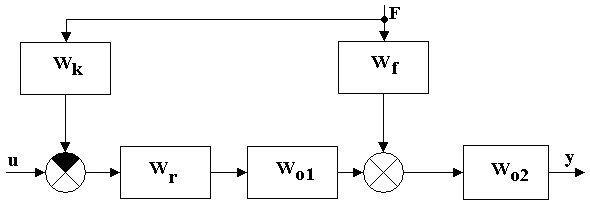
Рис. 14 Система с компенсатором
Таким образом, рассчитать компенсатор можно следующим образом:
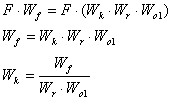
Рассчитаем дискретный компенсатор с помощью Matlab’а.
| W1=tf([0.9],[20 1],'td', 1) % задаем передаточную функцию W2=tf([1],[500 100 1],'td', 15) % задаем передаточную функцию Wf=tf([0.7],[10 1]) % задаем передаточную функцию Wob=W1*W2 % общая передаточная двух последовательных частей системы T=1 % время квантования Wdiskr=c2d(Wob,T,'zoh') % передаточная в дискретной области W1d=c2d(W1,T,'zoh') % передаточная в дискретной области W2d=c2d(W2,T,'zoh') % передаточная в дискретной области Wfd=c2d(Wf,T,'zoh') % передаточная в дискретной области [Numer Denom]=tfdata(Wdiskr, 'v') % находим числитель и знаменатель m=length (Numer) Denom1=Denom(2:m) Numer1=Numer(2:m) q0=1/sum(Numer1) for i=1:(m-1) q(i)=q0*Denom1(i) |
| p(i)=q0*Numer1(i) end Q=[q0 q] % матрица коэффициентов числителя P=[1 -p] % матрица коэффициентов знаменателя Wr=tf(Q, P, T) % передаточная функция регулятора Wkomp=(Wfd)/(Wr*W1d) % передаточная функция компенсатора [Nk Dk]=tfdata(Wkomp, 'v') % коэффициенты числителя и знаменателя [Nf Df]=tfdata(Wfd, 'v') % коэффициенты числителя и знаменателя [N1 D1]=tfdata(W1d, 'v') % коэффициенты числителя и знаменателя [N2 D2]=tfdata(W2d, 'v') % коэффициенты числителя и знаменателя |
Получим значение передаточной функции дискретного компенсатора:
![]()
Посмотрим на поведение системы при использовании такого компенсатора. Промоделируем поведение системы в Simulink’e.
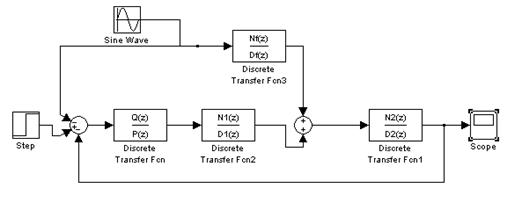
Рис. 15. Система без компенсатора
Получим следующую характеристику:
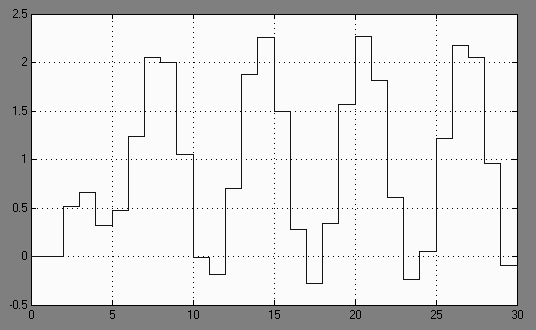
Рис. 16. Поведение системы без дискретного компенсатора
С дискретным компенсатором система примет вид:
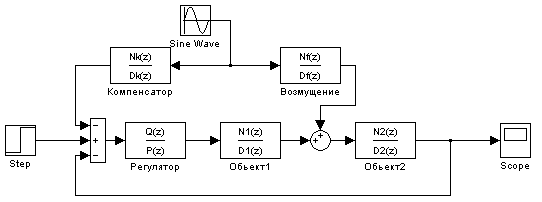
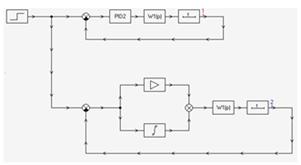
Рис. 17. Система с компенсатором
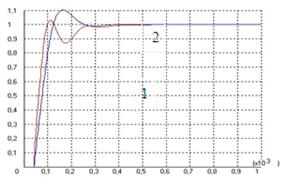
И характеристика будет следующей:
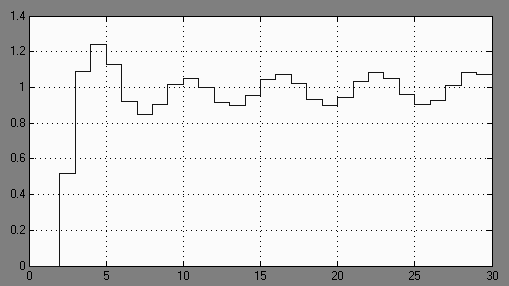
Рис. 18. Поведение системы с дискретным компенсатором
Как видно из характеристик, полученный дискретный компенсатор достаточно хорошо компенсирует возмущение.
6. Формирование интегрального квадратичного критерия
Любой критерий оптимальности есть аналитическая оценка оптимизируемого качества системы, зависящая от её параметров, задающих x и возмущающих f воздействий на объект управления u. Таким образом, критерий оптимальности выражается в виде функционала J(u), зависящего от функции управления, а оптимальное управление Uопт определяется как функция, реализующая экстремум критерия качества, т. е. функционал J(u).
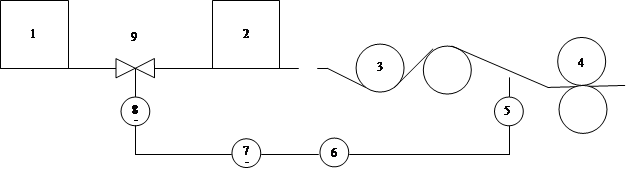
Изначально объект задан в виде:
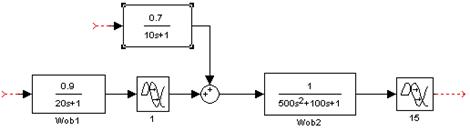
Рисунок 19 – Исходная модель объекта
Имеем систему, которая описывается моделью в области переменных состояния:
![]()
A, B, S – постоянные матрицы;x – ошибка по каждой из координат и равна:
![]()
Необходимо построить систему, которая обеспечит стабилизацию этих координат ![]() , т.е. сформировать оптимальный закон управления, минимизирующий функционал качества. Будем использовать квадратичный критерий вида:
, т.е. сформировать оптимальный закон управления, минимизирующий функционал качества. Будем использовать квадратичный критерий вида:
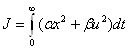
Поскольку система имеет не первый порядок, то будем использовать квадратичный функционал, который примет вид:
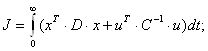
7.Синтез оптимального закона управления
Для начала необходимо перейти к модели переменных состояний. Для этого необходимо избавиться от запаздывания.
Разобьем запаздывание на 4 равных:
![]() .
.
Разложим экспоненту в ряд, ограничиваясь двумя первыми членами:
![]()
![]()
Таким образом, наше исходное запаздывание можно представить в виде четырех последовательно соединенных блоков и переходить в область переменных состояний от следующей модели:
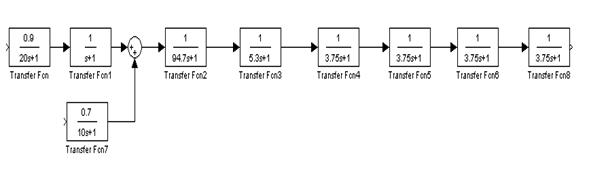
Рис.20.Вариант системы с учетом возмущающего воздействия и запаздывания
Передаточной функцию второй части объекта, в знаменателе содержит полином второго порядка, представим его в виде произведения двух полиномов первого порядка:
![]()
Таким образом, наше исходное запаздывание можно представить в виде четырех последовательно соединенных блоков и переходить в область переменных состояний от следующей модели:

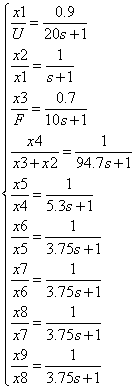
На основе полученных дифференциальных уравнений запишем матрицы A,B,S.
A=
![]()


C, D – единичные матрицы, служат в качестве весовых коэффициентов. B – управляющего воздействия, S – матрица возмущающего воздействия.
Функцию φ примем в виде:
![]()
где R– положительно определенная симметричная матрица
Воспользуемся уравнением оптимальности Беллмана:
![]() ,
,
Подставляя производные от φ и ![]() в формулу (4.9), получим:
в формулу (4.9), получим:
![]()
Оптимальный закон управления, минимизирующий выражение в скобках, равен:
![]()
Подставляя полученный закон управления в функциональное уравнение Беллмана, и приравнивая коэффициенты при одинаковых степенях переменных состояния, находим уравнения для нахождения матриц Rи L:
![]()
Видно, что в первом уравнении системы неизвестной является только матрица R, после её нахождения, на основании второго уравнения системы, можно найти матрицу L, которая представляет собой матрицу коэффициентов обратной связи по возмущению.
И так рассчитаем оптимальный регулятор, для этой цели используем математический пакет MatLab.
clc,clear,echo on
clc,clear,echo on
% Расчёт оптимального регулятора
% задание матрицы коэффициентов при переменных состояния
clc
clear
A=[-0.045 0 0 0 0 0 0 0 0;1 -1 0 0 0 0 0 0 0;0 0 -0.07 0 0 0 0 0 0;0 0.01 0.01 -0.01 0 0 0 0 0;0 0 0 0.18 -0.18 0 0 0 0;0 0 0 0 0.26 -0.26 0 0 0;0 0 0 0 0 0.26 -0.26 0 0;0 0 0 0 0 0 0.26 -0.26 0;0 0 0 0 0 0 0 0.26 -0.26];
B =zeros(9)
B(1,1)=0.045;
C=eye(9);
S=zeros(9);
S(3,1)=0.07;
D=eye(9);
R=0.5*eye(9);
Q=R;
% решение уравнения Рикатти
[X,L,G,RR]=care(A,B,Q)
% матрица коэффициентов обратной связи по возмущению
L=G*S*(-G*B-A')
В результате получаем коэффициенты обратной связи по переменным состояния:
G1= 0.5089 G5= 0.0139 G9= 0.0001
G2= 0.0175 G6= 0.0033
G3 = 0.0968 G7= 0.0012
G4= 0.6909 G8= 0.0003
Матрица L имеет вид
 ,
,
Построим модель для проверки работы рассчитанного регулятора.
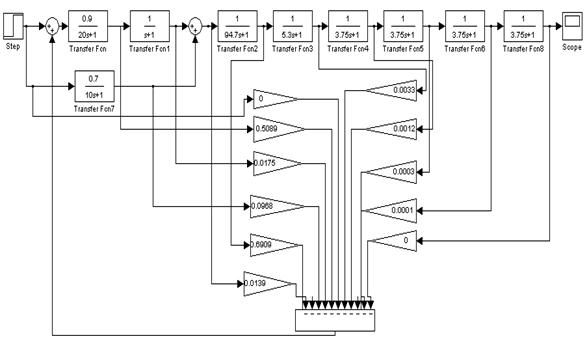
Рис.21. Модель системы с оптимальным регулятором
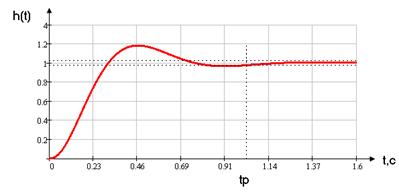
Получим следующий график переходного процесса:
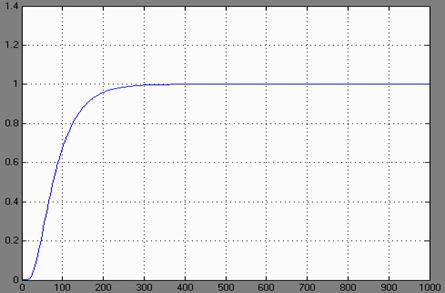
Рис.22.
Из рисунка можно сделать заключение о том, что регулятор осуществляет качественное управление, так как обеспечивает незначительную статическую ошибку (ε = 0.03).
Похожие работы
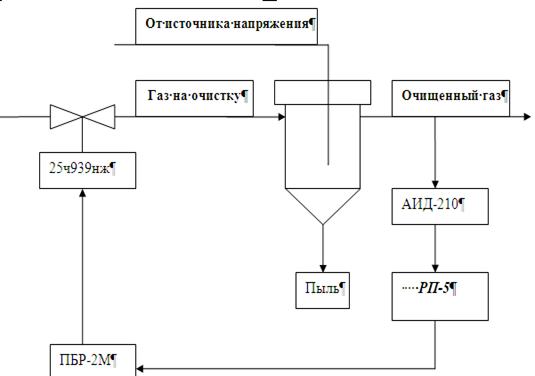
... параметры. Показателем эффективности данного процесса является степень очистки газа. Для решения задачи построена одноконтурная система управления процессом электрической очистки газа. Выбран регулятор и построена математическая модель системы управления. На модели определены оптимальные параметры регулятора. Выбраны приборы для основного контура регулирования. 1. Специальная часть ...
... поведение регулируемой величины. Управляющее воздействие вырабатывается устройством управления (УУ). Совокупность взаимодействующих управляющего устройства и управляемого объекта образует систему автоматического управления. Система автоматического управления (САУ) поддерживает или улучшает функционирование управляемого объекта. В ряде случаев вспомогательные для САУ операции (пуск, остановка, ...
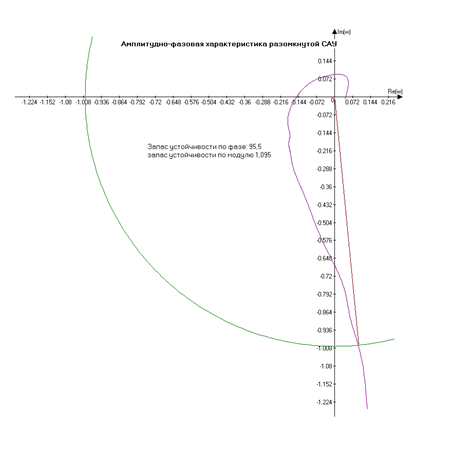
... устройства, которое нужно добавить к некоторой неизменяемой части системы, чтобы обеспечит требуемое качество системы в установившемся и переходном режимах. Наиболее приемлемым для решения задачи динамического синтеза является метод логарифмических амплитудных характеристик (метод ЛАХ). [1, § 12.5] Стадии синтеза по методу ЛАХ включают: 1. построение располагаемой ЛАХ, т.е. ЛАХ исходной ...
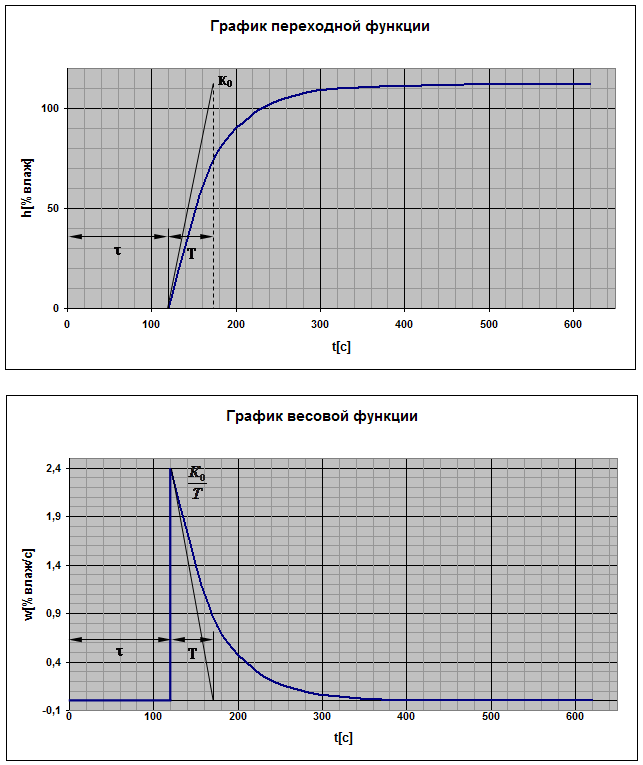
... воздействие) Δf(t) [%] - изменение концентрации массы (возмущающее воздействие) Δy(t) [г/м2] – изменение массы 1кв.м. полотна (выходная переменная) Временные характеристики по каналу управления. Передаточная функция объекта регулирования. Wоб(р) = К0 - коэффициент передачи - постоянная времени Т =50 с - запаздывание информации t =120 ...



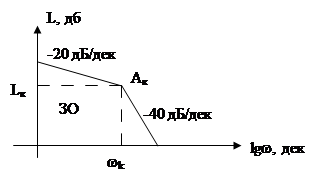

0 комментариев