Навигация
Перечень звеньев механизма
1.1.2 Перечень звеньев механизма
Звенья механизма связаны кинематическими парами:
1-2 – кинематическая пара 5-го класса, вращательная;
2-3 – кинематическая пара 5-го класса, вращательная;
3-4 – кинематическая пара 5-го класса, вращательная;
4-1 – кинематическая пара 5-го класса, вращательная;
5-1 – кинематическая пара 5-го класса, вращательная;
5-3 – кинематическая пара 5-го класса, вращательная;
4-5 – кинематическая пара 5-го класса, поступательная
Кинематические пары 4-го класса отсутствуют.
1.1.3 Определение степени подвижности механизма
Степень подвижности данного механизма определим по формуле Чебышева:
![]() , (1.1)
, (1.1)
где n – число подвижных звеньев механизма;
P5 – число пар 5 класса;
P4 – число пар 4 класса;
n=5; p5=7; p4=0.
![]()
Так как степень подвижности механизма равна 1, то для работы данного механизма необходимо одно ведущее звено.
1.2 Динамический анализ механизма
1.2.1 построение плана скоростей точек и звеньев механизма
Для определения скоростей точек и звеньев механизма применяем метод планов. Построение плана скоростей начинаем с ведущего звена механизма.
Посчитаем угловую скорость ведущего звена по формуле:
 , (1.2)
, (1.2)
n – частота вращения ведущего звена;
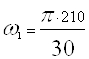 = 21 с-1.
= 21 с-1.
Поскольку известно, что его угловая скорость wОА – величина постоянная, то линейная скорость точки А равна:
VА=w11О1А=21×0,025=0,54 м/с, (1.3)
где lо1А – длина звена О1А в метрах;
Находим скорость точки А на плане скоростей. Направление вектора VОА перпендикулярно звену и направлен вдоль wо1А.
Из произвольно выбранной точки РV (полюс) откладываем вектор произвольной длины, численно равный вектору скорости VА. Определяем масштабный коэффициент скорости:
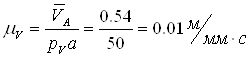 , (1.4)
, (1.4)
где VА – истинная скорость точки А, м/с;
рv×а– длина вектора на плане, мм.
Для определения скорости точки В воспользуемся условием принадлежности точки В звену АВ. Тогда можно записать следующее уравнение:
![]() , (1.5)
, (1.5)
где VА– известно и по величине, и по направлению;
VBА – известно лишь то, что линия действия этого вектора перпендикулярна звену АВ.
Эту прямую проведем на плане скоростей через точку а. В полюсе ставим точку В. Прямая будет параллельна оси АВ. Тогда:
![]() (1.6)
(1.6)
Скорость VВО2 направлена вдоль оси ВО2. На пересечении ВО2 и АВ будет находится точка В.
Численно скорость VВ равна:
![]() мм/с (1.7)
мм/с (1.7)
Поскольку точка Е принадлежит этому звену ВО2, то для векторов скоростей справедлива запись:
![]() (1.9)
(1.9)
где lBО2 и lBE – длины соответствующих звеньев.
На плане скоростей точка Е находится на отрезке bо2 и делит его в соответствии![]() .
.
Длина вектора, который соединяет полюс с точкой Е, отвечает вектор скорости VЕ, численное значение которой равно:
![]() мм/с (1.10)
мм/с (1.10)
Определяем скорость точки F, по формуле:
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
Вектором скорости точки D будет результатом общего решения векторных уравнений. В первом уравнении первое слагаемое известно по величине и по направлению.
Абсолютное значение скорости точки A, С, Е, F сведем в таблицу 1.1.
Определяем скорости центров масс по формуле :
![]() (1.13)
(1.13)
Значения скоростей центров масс занесем в таблицу 1.2.
Определение угловых скоростей звеньев механизма
Полученный план скоростей позволяет не только определить скорости всех точек механизма, а также величину и направление всех скоростей звеньев. Все линии плана, исходящие из точки ![]() , представляют собой абсолютные скорости точек. Периферийные линии – относительные скорости.
, представляют собой абсолютные скорости точек. Периферийные линии – относительные скорости.
Определим угловую скорость звена АВ:
![]() (1.14)
(1.14)
где VAВ – скорость движения точки A, относительно точки В.
Определим угловую скорость звена ВО2:
 (1.15)
(1.15)
Определим угловую скорость звена ED:
![]() (1.16)
(1.16)
Угловые скорости сведем в таблицу 1.1
Таблица 1.1 – Скорости точек и звеньев механизма
| VА | VВ | VE | VD | w2 | w3 | w4 |
| мм/с | мм/с | мм/с | мм/с | Рад/с | Рад/с | Рад/с |
| 0.54 | 0.3 | 0.21 | 0.12 | 5.25 | 1.75 | 5.16 |
| Vs1 | Vs2 | Vs3 | Vs4 | Vs5 | - | - |
| мм/с | мм/с | мм/с | мм/с | мм/с | - | - |
| 0.12 | 0.22 | 0.25 | 0.13 | 0.12 | - | - |
Масштабный коэффициент плана скоростей ![]()
Похожие работы
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... H 14 23,4 22 R, H 14 24,2 11,8 1 22,2 2. Расчет элементов кинематических пар на прочность. 2.1. Определение внешних сил, действующих на звенья. В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции ...
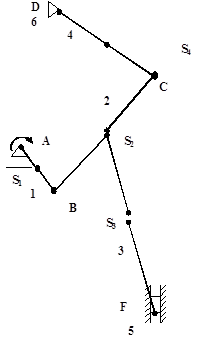

0 комментариев