Навигация
Определение уравновешивающей силы
1.3.3 Определение уравновешивающей силы
На кривошип O2A действует шатун с силой RA. Для определения уравновешивающей RA=-RA необходимо задать ее направление. Считается, что сила Fур перпендикулярна звену АO1.
Уравнение моментов всех сил, действующих на кривошип относительно точки (O1) имеет вид:
![]() (1.47)
(1.47)
Отсюда:
 H (1.48)
H (1.48)
![]() Н.м (1.49)
Н.м (1.49)
Полученные данные занесем в таблицу 1.4.
Таблица 1.4
| Fур, Н | Мур, Н×м |
| 28 | 0.7 |
2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ
В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими внешними усилиями являются силы инерции Fi, моменты инерции M и реакции в кинематических парах R. Под действием внешних сил звенья плоского механизма испытывают деформации. В данном механизме преобладают совместные деформации изгиба и растяжения.
Анализ нагруженной группы Асура 4-5 показывает, что звено 4 во время работы механизма испытывает совместное действие изгиба и растяжения. Для оценки прочности механизма необходимо при помощи метода сечений определить величину внутренних усилий, действующих в сечениях. Значения всех сил сведем в таблицу.
Таблица 2.1
|
|
|
| Mi |
|
|
| 14 | 25 | 21 | 0,021 | 13 | 30 |
2.1 Построение эпюр NZ, QY, MX
Нагруженность звена позволяет выделить два участка, чтобы использовать метод сечений для них. Использование метода сечений для нормальной силы NZ дает следующие уравнения:
I участок
![]() (2.1)
(2.1)
II участок
![]() (2.2)
(2.2)
По этим данным строим эпюру NZ.
Для поперечной силы QY на соответствующих участках записываются такие уравнения:
I участок
![]() (2.3)
(2.3)
II участок
![]() (2.4)
(2.4)
Согласно с полученными значениями строим эпюру QY.
Аналитические уравнения записываем также для изгибающего момента на участках I и II:
I участок
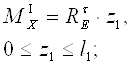
![]() (2.5)
(2.5)
![]()
II участок
 (2.6)
(2.6)
![]()
Эпюру МХ строим по полученным значениям моментов.
Из эпюр МХ и NZ видно опасное звено механизма.
Mmax =Нм
NZmax = H
2.2 Подбор сечений
Совмещенные деформации изгибания и растягивания являются причиной возникновения в материале нормального напряжения, которое определяется алгебраической суммой напряжений от изгибания и растяжения:
σmax = σ1 + σ2 = NZmax/F + Mmax/WZ (2.7)
где F – площадь сечения;
WZ – момент инерции сечения относительно оси Z.
Это напряжение σmax , согласно с условиями прочности, должно быть не больше допускаемого │σ│= 170 МПа:
![]() .
.
σmax = NZmax/F + Mmax/WZ ≤ │σ│ (2.8)
Это уравнение дает возможность найти геометрические размеры опасного разреза через подбор параметров F и WZ.
Будем рассчитывать для прямоугольного сечения. Тогда
Wx=bh2/6
h = 2b; F = hb=2b2; WZ = 4b3/6; (2.9)
b=![]() =5mm
=5mm
h=2b=2*5=10mm
Так как условие прочности выполняется, то полученный диаметр подходит.
Для круглого сечения используем отношения:
![]() ;
; ![]() ; (2.11)
; (2.11)
Отсюда находим диаметр:
d=![]() =3mm
=3mm
F=πD2/4 = 3.14![]() /4=7.06
/4=7.06
Для сечения в виде двутавра параметры находим подбором, подставляя в выражение (2.13) значение WX. Принимая [σ] = 70 МПа (латунь), выбираем двутавр с параметрами Н = 15 мм, В = 7 мм, S = 1.5мм, S1 = 1.5 мм, ГОСТ 13621-74, изготовленный из латуни.
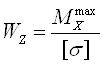 (2.13)
(2.13)
WZ= 0,245/70*106=0, 0035![]()
Выводы
В ходе выполнения курсовой работы были изучены методы анализа и расчета плоских рычажных механизмов. В результате динамического анализа были определены скорости, ускорения, силы и моменты, действующие на звено.
Расчет на прочность звеньев механизма показал наиболее опасные участки.
Исходя из конструкторских соображений, был изменен диаметр круглого сечения с 4,8мм на 5мм. Размеры прямоугольного сечения 5мм на 10 мм.
Подобрав сечения, определяем, что наиболее выгодным является сечение в форме двутавра, так как с точки зрения затрат материала наиболее выгодные сечения те, у которых большая доля материала размещена в верхней и нижней частях сечения где напряжения наибольшие и поэтому материал наиболее полно используется.
СПИСОК ЛИТЕРАТУРЫ
1 Степин П.А. Сопротивление материалов. Изд. 5-е, перераб. и доп. Учебник для студентов машиностроительных вузов. М., «Высшая школа», 1973.
2 Методические указания к курсовой работе по курсу «Теоретическая механика» для студентов специальностей 7.091807 и 7.091002 / Автор Евстратов Н.Д. – Харьков: ХТУРЭ, 2009. – 40 с.
3. Артоболевский И.И. Теория механизмов и машин. – М.: Наука, 2008.-640с.
4 Тарг С.М. Краткий курс теоретической механики. – М.: Высш. Шк. 1986.-416с.
5 Конспект лекций .
6 Анурьев В.И. Справочник конструктора-приборостроителя. – М.: «Приборостроение» 1967 688 с.
Похожие работы
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... напряжений; 4) определить размеры детали и округлить их до ближайших стандартных, согласно которым будет производится подбор сечений. 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Проектный расчет на прочность будем производить для группы Ассура 2-4 данного ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... H 14 23,4 22 R, H 14 24,2 11,8 1 22,2 2. Расчет элементов кинематических пар на прочность. 2.1. Определение внешних сил, действующих на звенья. В результате динамического анализа плоского рычажного механизма определены внешние силы, действующие на звенья и кинематические пары. Такими внешними усилиями являются силы инерции F , моменты инерции M , а также реакции ...
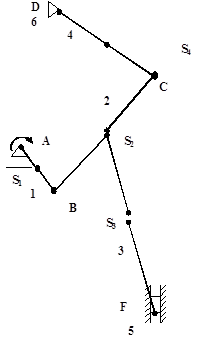

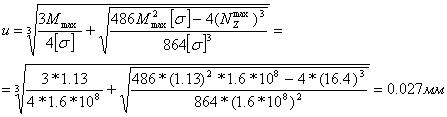
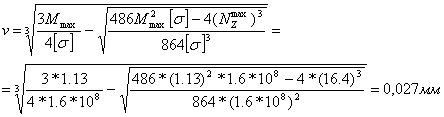
0 комментариев