Определение ускорений точек и звеньев механизма

1.2.2 Определение ускорений точек и звеньев механизма

Для определения ускорений точек применяем метод планов ускорений. Построение плана ускорений начинаем с ведущего звена механизма, учитывая, w – постоянная величина. Тогда ускорение точки А ведущего звена:

м/с², (1.17)

Определение масштабного коэффициента плана ускорений производится следующим образом:

м/с^2.мм, (1.18)

где p_аа – длина вектора в мм.

Векторное уравнение плоскопараллельного движения звена АВ с полюсом в точке А имеют вид:

(1.19)

где  – нормальная составляющая ускорения точки В в её относительном движении вокруг точки А;

 – тангенциальная составляющая ускорения точки В в её относительном движении вокруг точки А.

В этой векторной сумме ускорение точки А известно, нормальная составляющая ускорения движения точки В относительно точки А направлено от точки В к точке В и равно:

, (1.20)

А его длина на плане ускорений считается с учётом масштабного коэффициента по формуле:

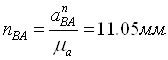, (1.21)

На плане ускорений с точки а вдоль звена АВ проводим вектор длинной nВА. О третьем составляющем векторного ускорения известно только направление – перпендикулярное звену. Потому на плане ускорений с конца вектора n_ВА проводим перпендикулярную линию.

Ускорение точки D найдем из звена ED. Тогда ускорение точки D равно:

(1.22)

В векторном уравнении 1.22 первое слагаемое известно, второе направлено от точки вдоль звена и численно равно:

 м/с (1.23)

Длина отрезка на плане ускорений:

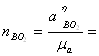 1.3 мм (1.24)

Найдем ускорение a_D из звена ED :

(1.25)

 м/с (1.26)

(1.27)

Значения ускорений точек и звеньев занесены в таблицу 1.2.

Угловые ускорения рассчитываются по формулам:

(1.28)

(1.29)

(1.30)

Для определения центра масс aS₁ звена ОА найдем на плане ускорения точку S1, по условию она лежит по средине звена, поэтому:

 м/c² (1.31)

Аналогично находим центры масс других звеньев:

(1.32)

(1.33)

(1.34)

(1.35)

Ускорения точек занесем в таблицу 1.2.

Таблица 1.2 – Ускорения точек и центров масс угловые ускорения звеньев механизма

аА	аВ	аЕ	аD	E2	E3	E4
мм/с2	мм/с2	мм/с2	мм/с2	1/с2	1/с2	1/с2
12.07	12,8	9,2	11,5	295	220	65
aD	aS2	aS3	aS4	-	-	-
1/с2	1/с2	1/с2	1/с2	-	-	-
5.6	4.6	9	6.4	-	-	-

Масштабный коэффициент плана ускорений – .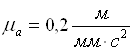

1.3 Кинетостатический анализ механизма 1.3.1 Определение сил инерции механизма

Если к механизму кроме внешних сил приложить силы инерции его звеньев, то условно можно считать, что механизм находится в равновесии. В этом случае для определения реакций в кинематических парах можно использовать уравнения статики, если в них включить силы инерции звеньев.

Сила инерции звена направлена в сторону, противоположную направлению ускорения центра масс этого звена и равна произведению массы этого звена на ускорение центра масс:

(1.36)

При этом существует также главный момент инерции звена, который приложен к центру масс звена и направлен в противоположную угловому ускорению звена сторону. Определяется по формуле:

(1.37)

где IS – момент инерции звена, для стержневого механизма , ;

Е– угловое ускорение звена, .

Силы инерции механизма приведены в табл. 1.3.

Таблица 1.3 – Рассчитанные значения сил и моментов инерции звеньев механизма

Fи2	Fи3	Fи4	Fи5
Н	Н	Н	Н
23	28,8	26,6	22,4

Масштабный коэффициент плана сил

где - длина вектора на плане сил