Формирование трехмерного оптического макроскопического
Формирование двумерного изображения
Формирование изображений методом кодирования апертуры
Трансаксиальная томография
Обработка сигналов
Представление изображений
Другие методы трехмерного отображения
Глубинные контуры
Распознавание образов
Операционные методы
Навигация
Операционные методы
Анализ и моделирование методов когерентной оптики в медицине и биологии
105404
знака
0
таблиц
19
изображений
6.1 Операционные методы
Имеются два отдельных способа использования преобразования Фурье для решения задачи распознавания образов. При первом способе (предназначенном для случаев последовательной обработки, а также для некоторых случаев параллельной обработки) мы можем измерить амплитудную (а иногда и фазовую) информацию, содержащуюся в Фурье-преобразовании и сравнить ее оптическими или электронными методами с аналогичными картинами для различных, ранее встречавшихся объектов. Оптически эта операция осуществляется помещением маски (позитивной или комплексной) в плоскость Фурье-преобразования и измерением прошедшего света. При использовании электронных методов сравнения в частотную плоскость помещают специальные фотодетекторы в виде секторов и колец [1.72]. При втором способе (он соответствует некоторым случаям параллельной обработки) мы можем использовать свет, прошедший через фильтр, для формирования изображения входной сцены. Изображение оказывается самым ярким для тех частей входной сцены, для которых через маску прошло больше всего света. Для равномерно освещенной сцены это означает, что объекты, наиболее близко соответствующие тест-объекту, использованному для изготовления маски, проявляют себя в виде ярких пятен. Ограничив этот отклик, мы можем определить местоположение и сосчитать объекты предварительно выбранной формы.
Изменения в размере объекта и его ориентации (относительно оптической оси) важны в разной степени для объектов разной формы, например вращение не оказывает существенного влияния при распознавании клеток, обладающих осевой симметрией. В любом случае вращение и изменение размера может быть выполнено либо физически, либо оптически (например, вращением «призмы Довэ), чтобы привести объект в соответствие с тест-объектом. Можно преобразовать преобразование Фурье в преобразование Меллина (инвариантное к масштабу объекта), а также и получить преобразование, инвариантное к вращению [1.73], путем соответствующего воздействия на входное изображение перед обработкой.
6.2 Применения
Имеются два тина областей применения когерентных оптических методов распознавания образов: во-первых, когда сцена, объект или образ очень сложны, чтобы можно было использовать удобные цифровые методы, и, во-вторых, когда высокая скорость измерения объекта исключает применение цифровых методов. В обоих этих случаях оптическое распознавание оказывается необходимым решением. Оптическое распознавание образов также является очевидным подходом к решению проблемы, когда измерения, которые должны быть выполнены, по своей природе оказываются оптическими.
Показательным применением когерентной оптики является автоматический счет ретикулоцитов с помощью согласованных фильтров, синтезированных на ЭВМ. Квалифицированный техник может сосчитать до 500 штук в минуту. С помощью когерентной оптики мы можем обработать почти мгновенно 1 млн. (это соответствует числу ретикулоцитов на площади реального предметного стекла диаметром 1,5 см) [1.74]. В данном случае используется параллельная обработка всех освещаемых клеток. Следовательно, метод работает благодаря наличию большого числа клеток, определенные усредненные свойства которых оказываются априори известными. Например, в большом поле с объектами спичкообразной формы часть этих объектов, ориентированная вертикально с точностью ±5°, предсказывается с высокой точностью. И наоборот, если мы измеряем число, таким образом, ориентированных объектов спичкообразной формы, мы можем подсчитать их полное число. Используемые в рассматриваемом случае пространственные фильтры искали определенные обобщенные образы ретикулоцитов, по всей вероятности, не заключающие в себе точно любую клетку, а Достаточно хорошо отображающие много клеток, чтобы обеспечить основу для счета. Реальный фильтр, несколько идеализированный, синтезировался на ЭВМ.
Другое применение, которое было продемонстрировано, связано с отображением рентгеновских изображений грудной клетки для постановки диагноза пневмокониоза (затемнения легкого) [1.75]. В этом случае критерием является увеличение высокочастотных компонент в пространственном спектре тенеграммы объекта с пневмокониозом. Аналогичные измерения были выполнены над рядом других изображений, интересующих медиков.
Вероятно, самым интересным применением для обработки данных была идентификация клеток (например, видов лейкоцитов) в жидкой системе [1.76]. В данном случае не формируется никакого изображения. Для освещения отдельных клеток используется свет разных длин волн, освещающий клетки при прохождении ими точки с фиксированным освещением. Часть света, дифрагированная каждой клеткой под разными углами, является мерой размеров и формы клеток. Поскольку обрабатывается большое число клеток, то статистический анализ может быть вполне точным. Конечно, перемещение объекта (всегда присутствующее по определению в жидкой системе) не вызывает изменений в картине Фурье-преобразования.
7. Выводы
Биомедицинские применения когерентной оптики многочисленны, эффективны, но случайны. Коммерческое использование когерентной оптики не предпринималось, не считая некоторых упомянутых ранее замечательных исключений.
8. Приложение: различные методы формирования трехмерных изображений
О формировании трехмерных изображений было сказано так много, что возможна некоторая путаница. Целью данного приложения является систематизация различных терминов и понятий с тем, чтобы они стали легкими для понимания и сравнения между собой.
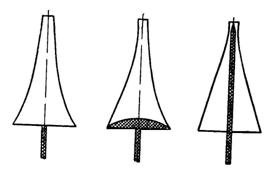
Пусть нам дан трехмерный объект, который может содержать и некоторую внутреннюю структуру. Каким образом мы можем его зарегистрировать на двумерном носителе? Существуют четыре основных способа решения этой проблемы. Во-первых, мы можем записать голограмму этого объекта. Голограмма зарегистрирует полную трехмерную информацию об объекте (за исключением теневых эффектов в плоских голограммах, которые исчезают в цилиндрической голограмме). Во-вторых, мы можем сжать одно измерение, чтобы обеспечить правильное изображение в двух измерениях и неясное в третьем. Метод проекций в рентгенотехнике даст хорошие иллюстрации этого. С помощью точечного источника излучения мы можем спроектировать на экран тень объекта (как это показано на рис. 8.1,а). Отметим, что для каждой точки теневого изображения мы можем провести прямую линию, соединяющую эту точку с точечным источником. Распределение поглощения излучения вдоль этой линии оказывается неопределенным (во всяком случае, известно только полное поглощение вдоль этой линии). Обычные рентгеновские изображения имеют именно такой характер. Назовем такие проекции двумерными проекциями (для достижения цели, поставленной в приложении). В отличие от этого один срез двумерной проекции (который мог бы быть получен с помощью расходящегося пучка в виде веера, как показано на рис. 8.1, б), мы назовем одномерной проекцией.
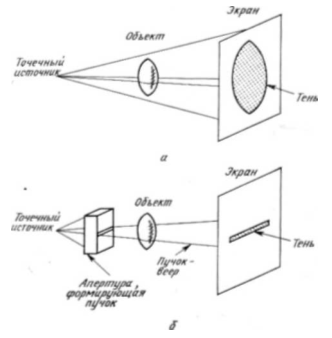
Рис. 8.1. Точечный источник создает конус направленных на объект лучен, которые и образуют на экране его теневое изображение (а). Если между точечным источником и объектом поместить щелевую диафрагму, то объект будет освещаться только веером лучей. В этом случае мы имеем трансаксиальное освещение, показанное на нижнем рисунке (б).
Получив проекции объекта (одно- и двумерные) с многих ракурсов и осуществив восстановление, мы можем синтезировать изображение трехмерного объекта (по его двумерным проекциям) или получить двумерное сечение этого объекта веерным пучком (по его одномерным проекциям). Примерами синтеза трехмерных изображений объекта по его двумерным проекциям являются псевдопараллаксные изображения, а также цилиндрические мультиплексные голограммы. Примером синтеза двумерного изображения объекта по его одномерным проекциям служит трансаксиальная томография. Во всех этих случаях дополнительное измерение синтезируется по многочисленным проекциям, полученным с многих направлений. В-третьих, мы можем совсем не учитывать одну координату из трех. Метод профилирования, является примером такого подхода. Обозначив поперечные координаты через х и у, а координату по глубине через z, получаем профили изображений в координатах х—z при постоянном у и в координатах у—z при постоянном х. И, наконец, в-четвертых, мы можем точно записать изображение в координатах х—у и восстановить затем координату z (измерение по глубине) некоторым образом (например, с помощью контуров по глубине.
Мы должны теперь уделить больше внимания голографии с малой числовой апертурой (которая включает акустическую голографию и формирование изображений методом кодированной апертуры). Предположим, что мы восстанавливаем изображение с голограммы, используя оптическое излучение с длиной волны л.
Если апертура голограммы равна А, а расстояние от голограммы до плоскости изображения D, то поперечное разрешение будет приблизительно лD/A, а глубина фокуса лD2/A2. Таким образом, части трехмерного изображения, разделенные, но глубине на расстояние, большее, чем лD2/A2, могут рассматриваться последовательно. Простейший способ реализации этой идеи состоит в перемещении экрана наблюдения в пределах реального изображения взад и вперед от голограммы.
Сейчас мы можем объяснить термин «томография». Томография стала означать метод формирования двумерных изображений поперечных сечений объекта. Она понятно и хорошо названа трансаксиальной томографией. Изображение оказывается томографическим, если освещение находится в плоскости сечения объекта. Назовем центральную нормаль к плоскости сечения его «осью». В этом случае мы видим причину использования слова «трансаксиальиый»: оно использовано для описания характера освещения. Последовательные плоскости по глубине, получаемые с кодограмм или акустических голограмм, оказываются аксиальными томографическими изображениями. К сожалению, иногда слово «аксиальный» используется тогда, когда следует употребить слово «трансаксиальный» (как, например, в аббревиатуре CAT — computerized axial tomography, что означает «цифровая аксиальная томография»), поэтому мы не оставили подходящего слова для такого рода томографии. Исследователи, работающие в области акустической голографии и формирования изображений с помощью кодированных апертур, просто ссылаются на свои «томографические» изображения.
Томографические изображения могут быть синтезированы голографически таким образом, что наблюдатель видит каждое томографическое изображение в правильном трехмерном соотношении к каждому другому томографическому изображению. Это не дает никакой новой информации, но помогает человеку-наблюдателю легче воспринимать информацию, уже имеющуюся в томографических изображениях.
Литература
1. Abbe Е., Arch. Mikrosk. Anat, 9, 413 (1873).
2. Gabor D., Nature, 161, 777 (1948).
3. Leits E. N.. Upatnieks J., /. Opt. Soc. Am., 52, 1123 (1962).
4. Toth L.. Collins S. A , Jr., Appl. Pht/s Letters, 13, 7 (1968).
5. Сох М.Е., Buckles R. G., Whitlow D., Appl. Opt., 12, 128 (1971).
6. McMahon D.H., Caulfield H. J., Appl. Opt., 9, 91 (1970).
7. Thompson B.J., /. Opt. Soc. Am., 53 (1963). Silverman В. Л., Thompson B. J., Ward J. H., У. Appl. Met., 3. 792 (1964).
8. Boettner E.A., Thompson B. J., Opt. Eng., 12, 56 (1973).
9. Singh К., Attl. Fond., 27, 197 (1972).
10. J. Opt. Soc. Am., 66, vol. 11 (1976).
11. Gara A.D., Majkowski R.P., Staplcton Т.Т., Appl. Opt, 12, 2172 (1973).
12. Balasubramanian N.. Opt. Eng., 14, 448 (1975).
13. Caulfield H.J. Hirschfcld Т., Weinberg J. M., Herron R. E., Proc. IEEE. 65. 84 (1977). [Имеется перевод: Колфнлд Г. и др. — ТИИЭР, 1977, т. 65 № I, с. 101.]
14. Rosen А.N.. Opt. Laser Tech., 7, 127 (1975).
15. McMahon D.II., Laser Focus, 6, 34 (1970), Appl. Opt, 11, 798 (1972).
16. Mueller R.K.. Acoustical Holography Survey, in: Advances in Holography, cd. by N. H.
17. Farhat, vol. 1, Dekker, New York, 1975.
18. Mueller R. Sheridon N. K-, Appl. Phys. Letters, 9, 328 (1966.)
19. Greguss P., Acoustica, 29, 52 (1973).
20. Landry J., Kcyani H., Wade G., Bragg Diffraction Imaging, in: Acoustical Holography, cd. by G. Wade, vol. 4, Plenum Press, New York, 1972.
21. Whitman R.L, Ahmed M., Korpel A., A Progress Report on the Laser Scanned Acoustic Camera, in: Acoustical Holography, Plenum Press, New York. 1974.
22. Mertz L., /. Opt. Soc. Am., 50, 505 (1960).
23. Young N. O., Sky and Telescope, 25, 8 (1963).
24. Chang L.Т., Macdonald В., Pcrcz-Mendez V., Proc. SP1E, 89. 9 (1977).
25. Gaskill J.D.. Whitehead F. R., Gray J. E., O'Mara R. E., Matched Filter Restoration of Coded Gamma and X-Ray Imaging, in: Applications of Optical Instrumentation in Medicine, SPIE, vol. 35, 1973.
26. Chang L.Т., Kaplan S. N.. Macdonald В., Perez-Mendcz V., Shiraishi L., /. Nucl. Med., 15, 1063 (1974).
27. Barrett H.H., /. NucL Med., 13. 382 (1972).
28. Barrett H. IL, Horrigan F. A., Appl. Opt, 12, 2686 (1973).
29. Rogers W.L., Coded Aperture Imaging in Nuclear Medicine, Review and Update, in: ERDA Conf. on Applications of X- and Y-Ravs. Ann Arbor, May 1976.
30. Akcasu A.Z.. May R. S.. Knoll G. F., Rogers W. L., Koral K. F.. Jones L. W., Opt Eng., 13, 117 (1974).
31. Zaklad H., Electronics, 14, 89. (1976).
32. Peters Т.M., IEEE Trans., BME-21, 214 (1974).
33. ВаггсЛ II.H.( Radiology, 104, 429 (1972).
34. Weiss IL, Three-Dimensional X-Ray Information Retrieving by Optical Filtering, in: Proceeding of the 1974 International Optical Computing Conference IEEE. 1974.
35. Bicdermann K., /. Opt. Soc. Am., 61. 1439 (1971).
36. Macovski A., Phys. Med. Biol., 19, 523 (1974).
37. Casasent D., Hybrid Processors, in: Optical Data Processing, ed. by S. Lee: Topics in Applied Physics, Springer, Berlin, Heidelberg, New York; IEEF Trans. Comput. C-24, 318 (1975).
38. Everett R.L., Lopez G., Anderson W.L., Simpson J.W., A Fourier Opticai Phonocardiogram Record-Analyze System, in: Proceedings of the San Diego Biomedical Svmposium. SPIE, vol. 1, 1972.
39. Shamir J.. Winzer G., Opt Acta, 19. 795 (1972).
40. Redman J.D., /. ScL Instr., 2. 651 (1969).
41. Greguss P.. Caulfield H.J., Science, 177, 422 (1972).
42. Falus M., Caulfield H.J., Greguss P., Laser and Unconventional Optics, 51, 3 (1974).
43. Caulfield H.J., Appl Opt, 9, 1218 (1970).
44. De Bitetto D.J.. Appl. Phys. Letters,Caulfield II.J., Lu S., The Applications of Holography, Wiley-Intersciencc, New York, 1970, Chap. VIII.
45. Benton S. A.. Opt. Eng., 14, 402 (1975).
46. Chapman J.A., Grundy S.M. W., Wolton W.P., Redman J.D., Three Dimensional Reconstructions from Electron Micrographs by Holography, in: l'roc. 5th Eur. Congr. on Electron Microscopy, 1972.
47. Redman J.D., Wolton W.P., Shuttleworth E., Nature, 220, 58 (1968).
48. Cross L., School of Holography, San Francisco, unpublished.
49. Upatnieks J.t Leonard C. D., Mattila E. S., Archival Storage of Three Dimensional Images, in: International Opt. Сотр. Conf., 1975, IEEE No. CH0941-5c.
50. Jeong Т.H., Rudolph R., Lockctt P.. /. Opt. Soc. Am., 56, 1203 (1966).
51. Какичашвнли Ш.Д., Ковалева A.H, Рухадзе В.А.— Опт. и спектроскоп. — 1968, 24, № 4, с. 627.
52. In the USA Apollo Lasers, Hadron, and International Laser Systems market such lasers.
53. Caulfield II.J., Hirschfcld Т., Weinberg J.M., Herron R., Proc. IEEE, 65, 84 (1977). [Имеется перевод: Колфилд Г. и др. — ТИИЭР, 1977, т. 65, №1, с. 101.]
54. Varner J.R., Holographic Contouring, Alternatives and Applications, in: Developments in Holography, SPIE, vol. 25, 1971.
55. Lu S., Hemstreet H.W., Jr., Caulfield II.J., Phys. Letters. 2514, 294 (1967).
56. Brooks R.E., Hcflinger L.O., Wucrkcr R.P., Brioncs R.H., Appl. Phys. Letters, 7, 92 (1965).
57. Felcppa E.J.t IEEE, BME-I9, 194 (1972).
58. Ebersole J.F., Opt. Eng., 14, 436 (1975).
59. Rounds D.E., Olson R.S., Booher J., Measurement of Cell Migration Index with a Ис-Ne Laser, in: Third Conference on the Laser, Anals of the N. Y. Acad. Scl., vol. 267, 1976.
60. Sol lid J.E., Opt. Eng., 14, 460 (1975).
61. Stetson K.A., Opt. Eng., 14, 482 (1975).
62. Burian K-, Firtze W., Schwomma W., Holographic Study of the Ear Drum, in: Symposium 1976 on Elcctro-cochleography and Holography in Medicine, Miinster, March 1976, A29.
63. Tonndorff J., Khanm S. H., /. Acoust. Soc. Am., 49, 120 (1971).
64. Hogmoen K-. Gundersen Т., Holographic Vibration Analysis of the Osskular Chain, in: Svmposium 1976 on Electro-cochleography and Holography in Medicine, Munster, March 1976, A30.
65. van Bally G., Trommclfell als Mittel zur Differentialdiagnose von Schallci-tungsstorungen MEDEX 76, 3rd International Exhibition and Congress on Medical Electrics and Bioenginccring, Basel, June 1976.
66. Wedenall P.R., cited in Greguss P., Opt. Laser Technol, 8, 153 (1976).
67. Mausler G., Schuenk Т., Seidel Holographic Deformation Measurement for Optimizing Hip-Joint Prosthesis, in: Symposium 1976 on Electro-cochleography and Ilolography in Medicine, Munster, March 1976, p. 7.
68. Vukicevic D., Hancevic J., Nikolic V., Vukiccric S., Application of Holographic Intcrferomctry in the Biomechanics of the Locomotor System, in: Symposium 1976 on Electro-cochleographv and Holography in Medicine, Munster, March 1976, p. 7.
69. 7.69. Bremble G.R.. Laker M.J., Hardinge K.A. Preliminary Study of Fracture Fixation Using Holographic Intcrferomctry, in: Holography in Medicine,
P. Greguss, IPC Science and Tech. Press. Richmond, England, 1975, pp. 65—68.
70. Greguss P., Opt Laser Technol., 8, 153 (1976).
71. Vander Lugt A., IEEE Trans., IT 10. 139 (1964); Caulfield H J., Holographic Pattern Recognition — New Thoughts on Old Problems, in: Holography and Optical Filtering, NASA SP-299 (1973).
72. Thomasson S.Т., Middleton Т.J., Jensen N.. Coherent Optics in Mapping, SPIE, vol. 45, 1974; also George N.. Thomasson Т., Spindel A., U. S. Pat. 3689772 (1972).
73. Casasent D., Psaltis D., Appl. Opt, 15, 1795 (1976).
74. Shi N.K., Carlson F.P., IEEE Trans., BME-23, 84 (1976).
75. Kruger R.P.. Thompson W.В.. Turner Л.F., IEEE Trans, SMC-4, 40 (1974).
76. Salzman G.C, Crowell J.M., Goad C.A., Hansen К.M., Hiebert R.D., La Baure P.M., Martin J. C, Ingram M. L., Mullaney P.F., Clinical Medicine, 21 (1975).
Похожие работы
... матрице, имеющей частично историческую и социокультурную обусловленность. ГЛАВА 3 Логика и математика как связующее звено между философией и наукой Философский стиль мышления современного естествоиспытателя может быть представлен на основе идей Дж. Смарта и В. Куайна [1] в виде сферы взаимодействия классических и современных философских идей и теоретического естествознания в ...
... философии - особенно с методологических позиций материалистического понимания истории и материалистической диалектики с учетом социокультурной обусловленности этого процесса. Однако в западной философии и методологии науки XX в. фактически - особенно в годы «триумфального шествия» логического позитивизма (а у него действительно были немалые успехи) - научное знание исследовалось без учета его ...
... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...
... школа, 1988. 10. Артюхов В.Г., Ковалева Т.А., Шмелев В.П. Биофизика. Воронеж: Воронежский гос. ун-т 1994. 11. Антонов В.Ф. Биофизика. VI.: Арктос-Викапресс, 2000. 12. Дополнительная 13. Механика и биомеханика 14. Никитин E. VI. Теоретическая механика. VI.: Наука. 1968. Александер Р. Биомеханика. VI.: Мир. 1970. 15. Журавлева А.И., Iраевская И.Д. Спортивная медицина и лечебная ...
0 комментариев