Навигация
Нормальные формы логических уравнений. Преобразование логических уравнений к заданному базису
6. Нормальные формы логических уравнений. Преобразование логических уравнений к заданному базису
Если при проектировании логических схем предъявляется требование получения максимального быстродействия, логическая схема строится на основе представления ПФ в нормальной алгебраической форме.

Всего существует 8 нормальных форм представления ПФ. Получим их на примере проектирования мажоритарной логической схемы (мажоритарного элементы) “2 из 3”, пронумеруем и дадим символьное обозначение путем указания операций первого и второго этапов логического преобразования.
Таблица истинности для мажоритарного элемента приведена в табл.2, карта Карно на рис.5. МДНФ для этой функции является первой нормальной формой. Следующие три нормальных формы получим путем последовательного преобразования МДНФ с применением тождеств двойной инверсии и теоремы де-Моргана. МКНФ – пятая нормальная форма, остальные получены путем ее преобразования.
![]() = 1) И / ИЛИ
= 1) И / ИЛИ
![]() =
=![]() 2) И-НЕ / И-НЕ
2) И-НЕ / И-НЕ
=![]() 3) ИЛИ / И-НЕ
3) ИЛИ / И-НЕ
![]() . 4) ИЛИ-НЕ / ИЛИ
. 4) ИЛИ-НЕ / ИЛИ
![]() 5) ИЛИ / И
5) ИЛИ / И
=![]() =
=
= ![]() = 6) ИЛИ-НЕ / ИЛИ-НЕ
= 6) ИЛИ-НЕ / ИЛИ-НЕ
=![]() =7) И / ИЛИ-НЕ
=7) И / ИЛИ-НЕ
=![]() .8) И-НЕ / И
.8) И-НЕ / И
При проектировании логических схем в зависимости от наличия определенного типа элементов (базиса) используется соответствующая нормальная форма.
7. Скобочные формы логических уравнений
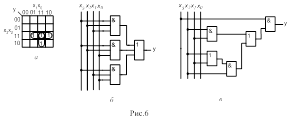
Для аналитического представления переключательных функций можно использовать не только нормальные формы, но и так называемые скобочные формы представления функций. Скобочные формы получаются путем тождественных преобразований МДНФ (МКНФ) с использованием скобок, изменяющих порядок (последовательность) логических преобразований. При вынесении общих членов за скобки порядок функции увеличивается. В практике проектирования логических схем к скобочным формам приходится обращаться в двух случаях: а) когда необходимо уменьшить аппаратные затраты и стоимость при реализации схем на логических элементах; б) когда число переменных и термов велико и реализация функций на основании МДНФ (МКНФ) с использованием стандартных логических элементов (с стандартным числом входов) невозможна. На рис.6,а представлена карта Карно логической функции, МДНФ которой
y = x3 x2 x1 ![]() x3 x2 x0
x3 x2 x0 ![]() x3 x1 x0 .(8)
x3 x1 x0 .(8)
Этой функции соответствует логическая схема второго порядка, показанная на рис.6,б. На основании законов дистрибутивности функцию (8) можно представить в форме
y = x3 [ x2 ( x1![]() x0 )
x0 )![]() x1 x0 ],(9)
x1 x0 ],(9)
которой соответствует схема на рис.6,в. В этой схеме максимальное число последовательно включенных логических элементов равно четырем, т.е. логическая схема имеет четвертый порядок. Каждый логический элемент имеет конечное быстродействие, которое характеризуется задержкой распространения сигналов от входа к выходу. Чем выше порядок логической схемы, тем больше задержка сигналов, тем ниже быстродействие схемы. Это недостаток логических схем, реализованных на основе скобочных форм ПФ.
Положительное свойство таких схем – меньшая сложность (аппаратные затраты) и стоимость.
Существует несколько способов оценки сложности логических схем: сложность по Квайну, определяемая как суммарное число входов всех логических элементов; сложность, как число логических элементов; сложность как число условных стандартных корпусов микросхем.
Так, суммарное число входов логической схемы четвертого порядка (рис.6,в) равно 10, а логической схемы второго порядка (рис.6,б) – 12.
В общем случае быстродействие и сложность схемы (стоимость) жестко связаны, при проектировании логических схем можно “обменять” быстродействие на стоимость и наоборот.
Второй пример необходимости использования скобочной формы ПФ рассмотрим на примере проектирования мажоритарного элемента “2 из 3” в двух вариантах: когда допустимо использовать логические элементы И-НЕ с любым необходимым числом входов и когда можно использовать только 2-входовые логические элементы И-НЕ.
В минимальной ДНФ логическая функция мажоритарного элемента в базисе И-НЕ имеет вид
y = ![]() .(10)
.(10)
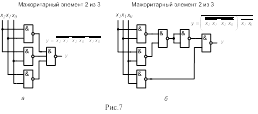
Этому уравнению соответствует логическая схема второго порядка рис.7,а, в которой используются 2- и 3-входовые элементы И-НЕ.
Если для реализации схемы разрешается использовать только 2-входовые элементы И-НЕ, то уравнение (10) преобразуется в скобочную форму
y =![]()
![]() ,(11)
,(11)
которому соответствует логическая схема четвертого порядка рис.7,б, которая хуже схемы рис.7,а по характеристикам быстродействия и сложности. Ухудшение характеристик оправдывается только возможностью реализации схемы на заданных стандартных элементах.
8. Комбинационные схемы
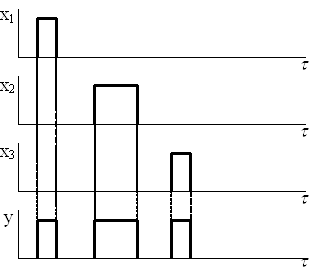
Логическая схема (рис.8) с n входами и k выходами реализует систему переключательных функций y0 ...yk-1. Каждая функция yi(x0 ...xk-1) однозначно соответствует входным наборам сигналов, комбинациям входных сигналов. Такие цифровые устройства образуют класс комбинационных схем (КС). Их часто называют схемами без обратных связей, или схемами без элементов памяти.

КС с несколькими выходами может быть представлена в виде совокупности схем, у каждой из которых лишь один выход. Работа каждого выхода описывается либо таблицей истинности, либо логическим уравнением.
В цифровой технике применяется большое число типовых (стандартных) КС, выполненных в виде интегральных схем малой и средней степени интеграции. Все многообразие КС, применяемых в цифровых устройствах, можно классифицировать по их основному функциональному назначению – по типу логической задачи, которую может решать КС в цифровом устройстве. По функциональному признаку можно сформировать следующие группы КС.
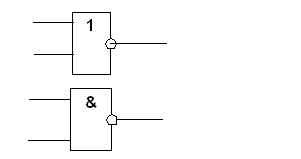
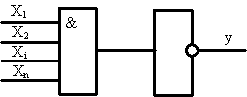
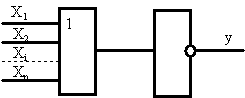
Логические элементы (ЛЭ) общего назначения, выпускаемые в виде готовых интегральных логических схем малой степени интеграции. К ним относятся ЛЭ, представленные на рис.9. Они образуют технически полную систему элементов, т.е. удовлетворяющую требованиям функциональной и физической полноты.
Функционально полная система элементов – система позволяющая реализовать любые, сколь угодно сложные ПФ путем представления их через типовые (базисные) функции. Физически полная система элементов – система, обеспечивающая работоспособность и надежное взаимодействие элементов при всевозможных комбинациях связи между ними (совместимость входных и выходных сигналов при воздействии на элемент нагрузок и дестабилизирующих факторов, при разбросе параметров и характеристик элементов и т.п.).
Преобразователи кодов – дешифраторы, детекторы состояний, шифраторы, преобразователи специальных кодов, ПЗУ и др.
Коммутационные узлы – ключи, мультиплексоры, мультиплексоры-демультиплексоры и др.
Арифметические узлы – схемы контроля на четность, сумматоры, схемы ускоренного переноса, арифметико-логические устройства, числовые компараторы, умножители и др.
Основными задачами изучения КС являются задачи анализа и синтеза этих схем. Задача анализа – нахождение функции, реализуемой конкретной схемой. Задача синтеза – преобразование заданной логической функции к форме, в которой ПФ представлена через логические функции заданных для реализации элементов. Например: через логические функции ЛЭ основного базиса, универсального базиса; через логические функции, реализуемые дешифратором, мультиплексором и т.п.

Список литературы
1.Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учеб. пособие для втузов. СПб.: Политехника, 1996.
2.Угрюмов Е.П. Цифровая схемотехника. СПб.: БХВ-Петербург, 2001.
3.Потемкин И.С. Функциональные узлы цифровой автоматики. М.: Энергоатомиздат, 1988.
4.Голдсуорт Б. Проектирование цифровых логических устройств: Пер. с англ. М.: Машиностроение, 1985.
Похожие работы
... базис применением теорем де Моргана в любой последовательности. Последнее справедливо, в силу того, что применение теорем де Моргана не изменяет числа букв в выражении. 3.Проектирование комбинационных схем с учетом коэффициентов объединения по входу и выходу Допустимая величина коэффициента объединения по входу (І) в реальных условиях проектирования КС оказывает существенное влияние на ...
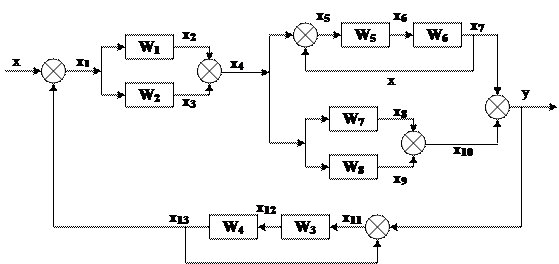
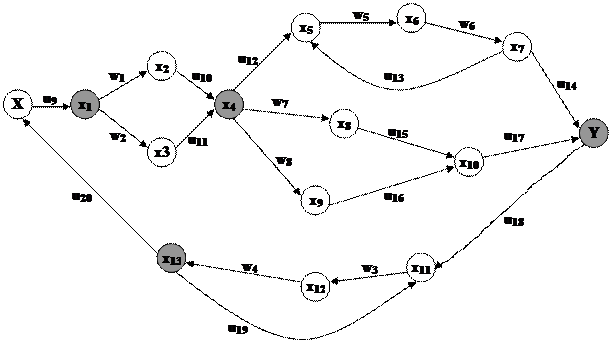
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... 1 1 0 1 0 0 14 1 1 1 0 0 0 15 1 1 1 1 0 1 Для выполнения синтеза логической схемы необходимо произвести следующие действия: 1.по таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ; 2.для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ и СКНФ, используя метод непосредственных преобразований; 3. ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...



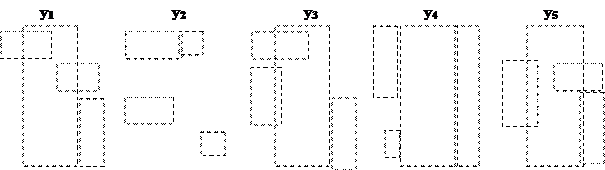

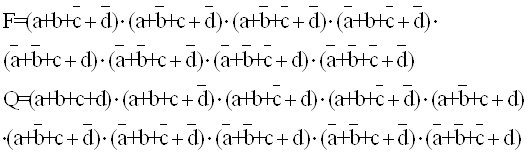

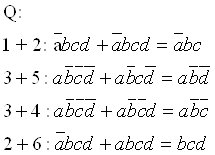
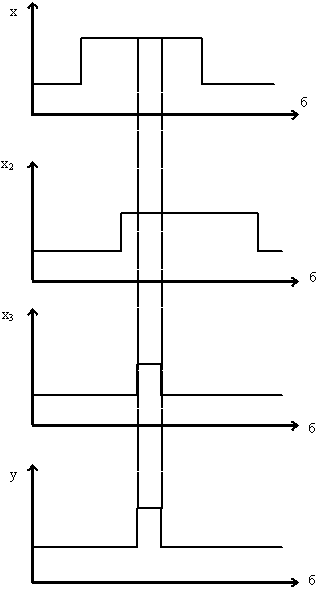
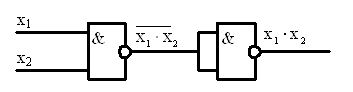
0 комментариев