Навигация
Не полностью определенные переключательные функции
3. Не полностью определенные переключательные функции
ПФ y(xn-1... x0) называется полностью определенной, если ее значения 0 или 1 заданы на всех 2n наборах. Если же значения функции не заданы хотя бы на одном наборе, то она называется не полностью определенной.
Значения функции могут считаться неопределенными, если:
а) в процессе работы логической схемы на ее входы никогда не подаются некоторые наборы сигналов, и, следовательно, функции y в таких случаях можно приписать неопределенные значения; б) разработчика логической схемы не интересует, какое значение примет выходной сигнал при некоторых наборах входных сигналов; в) при некоторых наборах входных сигналов значения выходного сигнала логической схемы 0 и 1 вызывают один и тот же результат в логическом устройстве, для которого он используется в качестве входного.
На рис. 1,д приведена карта Карно для не полностью определенной ПФ. Функция не определена на двух наборах: x3 = 1, x2 = 0, x1 = 0, x0 = 1 и x3 = 0, x2 = 1, x1 = 1, x0 = 0. Не определенные значения функции обозначаются символом ![]() или
или![]() . Обозначенные такими символами клетки карты Карно будем называть факультативными.
. Обозначенные такими символами клетки карты Карно будем называть факультативными.
Не полностью определенные функции можно доопределить произвольно , полагая y = 0 или y = 1.
4. Построение комбинационной логической схемы по заданной переключательной функции
Структурные формулы для заданной ПФ позволяют осуществить переход к тому цифровому логическому устройству, которое выполняет логические операции, входящие в структурную формулу.
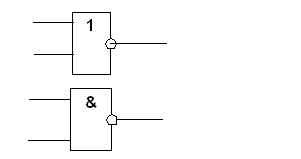
Например, для реализации выражения (1) требуются 3 элемента НЕ (для получения инверсий переменных - ![]() ), 4 трехвходовых элемента И (для получения конъюнкций –
), 4 трехвходовых элемента И (для получения конъюнкций –
![]() ,
, ![]() ,
, ![]() ,
,![]() )
)
и 1 четырехвходовый элемент ИЛИ (для получения логической суммы перечисленных четырех конъюнкций). Для реализации выражения (3) требуются 3 двухвходовых элемента И и 1 трехвходовый элемент ИЛИ.
Сказанное приводит к выводу, что при прямом способе построения логического устройства на основе использования структурной формулы, сложность логического устройства определяется сложностью структурной формулы. Одна и та же ПФ может быть реализована устройствами, отличающимися как своей структурой, так и сложностью (числом логических элементов).
Задача проектировщика состоит не только в том, чтобы создать устройство, выполняющее заданную ПФ, но и в том, чтобы из всех возможных вариантов выбрать наилучший, требующий меньшего числа элементов для реализации. При этом могут улучшаться не только технико-экономические (стоимость, масса, габариты), но и чисто технические показатели (например, быстродействие) разрабатываемого устройства, так как длинные цепи логических элементов вносят большее время задержки сигнала на выходе при переключениях устройства.
Проектируемое устройство должно быть оптимальным по количеству используемых для его построения элементов, а также количества их типов. Количество типов логических элементов определяет степень унификации схемных и конструктивных решений. Максимальная унификация достигается в том случае, если в логической схеме используются элементы только одного типа.
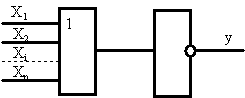
При прямом способе реализации ПФ (1), например, требуются логические элементы трех типов: НЕ, И, ИЛИ. Система логических элементов НЕ, И, ИЛИ достаточна для построения логических схем любой сложности. Такую систему называют функционально полной системой логических элементов (элементы НЕ, И, ИЛИ образуют основной логический базис).
Используя принцип двойственности и тождества алгебры логики, можно получить функционально полную систему, включающую два или даже один тип логических элементов. Например, элементы НЕ и И образуют логический базис. Элементы НЕ и ИЛИ также образуют логический базис.
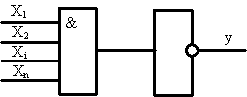
Базис, включающий только один тип логических элементов, называется универсальным. Универсальный базис образуют, например, логические элементы И-НЕ. Двухвходовый элемент И-НЕ выполняет логическую операцию ![]() . Универсальность элемента доказывается тем, что все три функции НЕ, И, ИЛИ основного базиса могут быть выражены через функцию И-НЕ:
. Универсальность элемента доказывается тем, что все три функции НЕ, И, ИЛИ основного базиса могут быть выражены через функцию И-НЕ:
![]()
Элементы ИЛИ-НЕ, выполняющие операцию ![]() , также являются универсальными. Операции НЕ, И, ИЛИ выражаются через операцию ИЛИ-НЕ следующим образом:
, также являются универсальными. Операции НЕ, И, ИЛИ выражаются через операцию ИЛИ-НЕ следующим образом:
![]()
Таким образом, задача синтеза логической схемы по заданной переключательной функции разделяется на две самостоятельные задачи:
получение структурной формулы в простейшей (минимальной) нормальной форме (МНФ); 2) преобразование МНФ к заданному логическому базису.
Похожие работы
... базис применением теорем де Моргана в любой последовательности. Последнее справедливо, в силу того, что применение теорем де Моргана не изменяет числа букв в выражении. 3.Проектирование комбинационных схем с учетом коэффициентов объединения по входу и выходу Допустимая величина коэффициента объединения по входу (І) в реальных условиях проектирования КС оказывает существенное влияние на ...
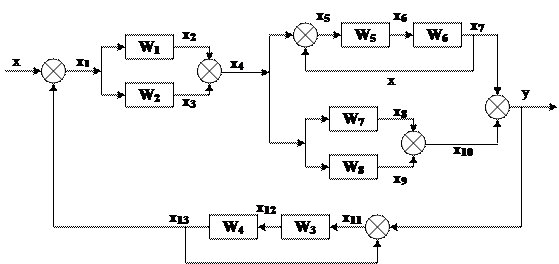
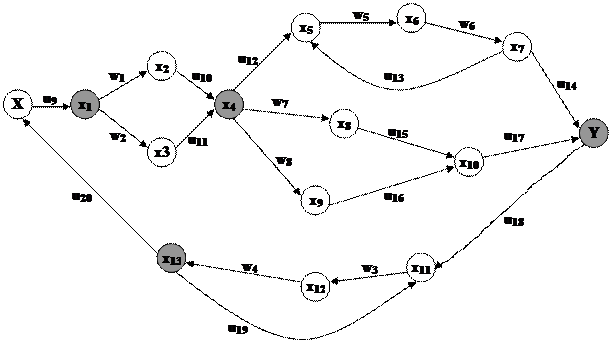
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
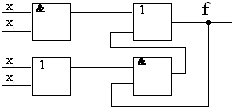
... 1 1 0 1 0 0 14 1 1 1 0 0 0 15 1 1 1 1 0 1 Для выполнения синтеза логической схемы необходимо произвести следующие действия: 1.по таблице истинности составить логические уравнения для каждого выхода в виде СДНФ и СКНФ; 2.для получения наиболее простой логической схемы выполнить минимизацию функций, записанных в СДНФ и СКНФ, используя метод непосредственных преобразований; 3. ...
... чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD. 1. Основы математического аппарата анализа и синтеза комбинационных логических устройств Все устройства, оперирующие с двоичной информацией, подразделяются на два класса: - комбинационные (дискретные автоматы без памяти). - ...



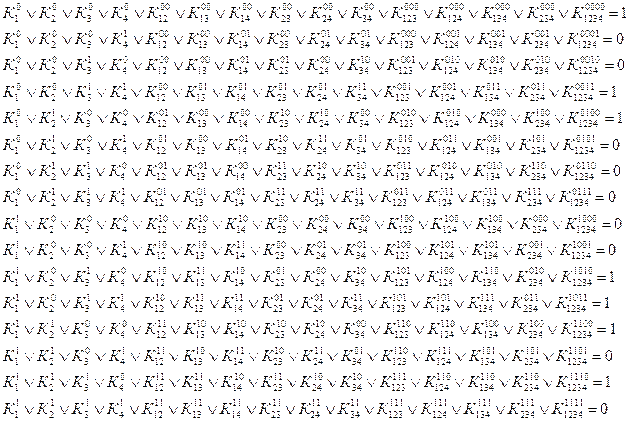
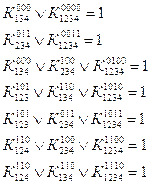
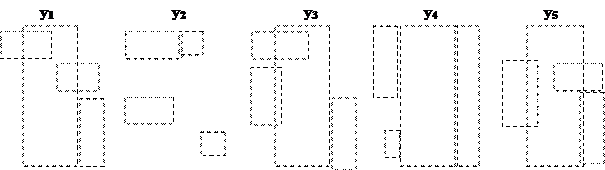

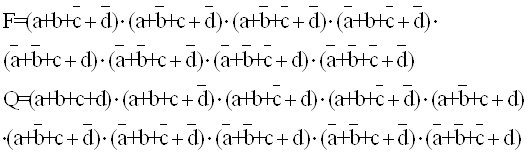

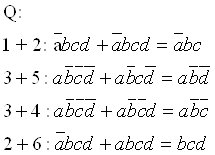
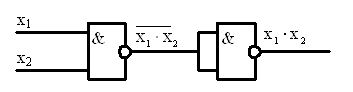
0 комментариев