Навигация
Теоретические основы методов отсечения
2. Теоретические основы методов отсечения
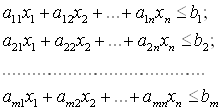
Запишем общую задачу целочисленного программирования: в области, определенной условиями
![]() (11)
(11)
![]() (12)
(12)
![]() - целые,
- целые, ![]() (13)
(13)
максимизировать функцию
![]() (14)
(14)
Назовем для кратности задачу (11–14) (£ц, C) – задачей. Соответствующую ей задачу без требования целочисленности переменных, т.е. задачу (11, 12, 14) назовем (£, C) – задачей. Поставим вопрос: нельзя ли решение (£ц, C) – задачи получить путем решения некоторой специальным образом построенной задачи без требования целочисленности переменных и такой, что оптимальные решения исходной (£ц, C) – задачи и задачи без требований целочисленности переменных будут совпадать. Другими словами: нельзя ли хорошо изученный аппарат решения задач линейного программирования приспособить к решению целочисленных задач. Принципиальный ответ на этот вопрос дает следующая теорема.
Теорема. Пусть £ – многогранник, £ц – множество его целых точек, R – выпуклая, линейная оболочка множества £ц, тогда:
1) R=Rц – целочисленный многогранник;
2) Rц = £ц;
3) R* – множество опорных решений задачи (£ц, C) содержится в многограннике Rц.
Доказательство. Докажем, что R – целочисленный многогранник. По условию теоремы £ – многогранник, поэтому множество его целых точек (оно обозначено через £ц) конечно. Поскольку R – выпуклая линейная оболочка этого конечного множества точек, R – тоже многогранник.
По самому определению выпуклой линейной оболочки, она содержит все опорные планы множества, на которое она натянута, т.е. многогранник R содержит все целочисленные точки £ц. Поэтому R – целочисленный многогранник. Обозначим его через Rц. Первая часть теоремы доказана.
Докажем, что Rц совпадает с £ц. Так как R – выпуклая оболочка точек множества £ц, то £ц ÍRц.
Покажем, что справедливо также и противоположное неравенство–включение, т.е. RцÍ£ц. Для этого выберем некоторый произвольный элемент х°ÎRц. Поскольку Rц содержит все опорные решения задачи (£ц, C), то х° удовлетворяет условиям задачи (£ц, C), т.е. х°Î£ц. Но поскольку произвольный элемент из Rцпринадлежит £ц, то очевидно, что справедливоRцÍ£ц. Сопоставляя противоположные включения RцÍ£ц и £цÍRц приходим к выводу: что £ц=Rц. Вторая часть теоремы также доказана.
Доказательство 3-го пункта теоремы является совершенно очевидным. Так как R* – множество опорных решений задачи (£ц, C), то R*Í£ц но £ц=Rц, поэтому R*ÍRц
Теорема доказана.
Следствием из этой теоремы является тот вывод, что оптимальное решение задачи, областью определения которой является выпуклая оболочка, натянутая на область поиска целочисленного решения, совпадает с оптимальным решением исходной целочисленной задачи.
Доказанная теорема и следствие из нее показывают принципиальную возможность замены решения задачи типа (£ц, C) некоторой процедурой построения и решения вспомогательной задачи типа (£, C), однако не дают алгоритма решений. К тому же построение выпуклой оболочки множества £ц реальных задач – чрезвычайно сложная, а подчас практически неразрешимая задача,
В 1954 г. Дж. Данциг высказал идею о том, что построение выпуклой оболочки целочисленной области для задачи (£ц, C) можно осуществлять поэтапно и решать получаемые при этом задачи. Однако при этом возникли вопросы как строить ограничения новой задачи и как обеспечить конечность процесса.
Ответ на эти вопросы был впервые получен Р. Гомори, который предложил алгоритмы решения целочисленных и. частично целочисленных задач.
Алгоритм Р. Гомори состоит из следующих процедур:
1. Решается (£, C) – задача, соответствующая исходной (£ц, C) – задаче.
2. Полученное оптимальное решение (£, C) – задачи, если оно существует, проверяется на целочисленность. Если условие целочисленности выполняется по всем переменным, то оптимальное решение (£, C) – задачи есть оптимальное решение (£ц, C) – задачи. Если условие целочисленности не выполняется хотя бы по одной координате, то переходят к третьему этапу. Если (£, C) – задача, оказывается неразрешимой, то (£ц, C) – задача тоже решения не имеет.
3. Строится дополнительное ограничение, обладающее тем свойством, что с его помощью отсекается часть области, в которой содержится оптимальное решение (£, C) – задачи и не содержится ни одного допустимого решения (£ц, C) – задачи. Процесс построения дополнительных ограничений и решения получаемых при этом (£, C) – задач продолжается до тех пор, пока не получим целочисленного решения или не убедимся в неразрешимости задачи.
При этом свойства, которыми должно обладать каждое из дополнительных ограничений при переходе от одной задачи к другой следующие:
1) дополнительное ограничение должно быть линейным, чтобы оставаться в области применимости аппарата линейного программирования;
2) дополнительное ограничение должно отсекать часть области, в которой не содержится допустимых решений целочисленной (£ц, C) – задачи, но есть найденное оптимальное решение нецелочисленной (£, C) – задачи, т.е. ограничение должно обладать свойством правильности, которое не позволяет потерять оптимальное решение исходной (£ц, C) – задачи.
Пусть х (£, C) – оптимальное решение (£, C) – задачи, которое является недопустимым решением для (£ц, C) – задачи. Неравенство
![]() (15)
(15)
определяет правильное отсечение, если удовлетворяет
а) условию отсечения: x(£, C) удовлетворяет неравенству (15)
б) условию правильности: любое допустимое решение задачи (£ц, C), удовлетворяет неравенству (15).
Методы, основанные на использовании процедуры построения правильных отсечений, получили название методов отсечения.
Похожие работы
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
... план будет найден. Заключение. Задачи экономической науки, требующие применения математики Имеется ряд определений предмета экономической теории. Из них вытекает необходимость экономико-математических методов, причем требуется самая изощренная современная математика, как теоретическая, так и прикладная. Фактически существует такая дисциплина, как математическая экономика, которая у ряда ...
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
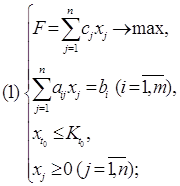
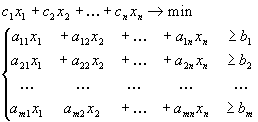
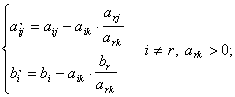


0 комментариев