Топологическая определяемость верхних полурешёток

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Топологическая определяемость верхних полурешёток.

Выполнил:

студент V курса математического факультета

Малых Константин Леонидович

Научный руководитель:

кандидат физико-математических наук, доцент кафедры алгебры и геометрии В.В. Чермных

Рецензент:

доктор физико-математических наук, профессор, заведующий кафедрой алгебры и геометрии Е.М. Вечтомов

Допущена к защите в государственной аттестационной комиссии

«___» __________2005 г. Зав. Кафедрой Е.М. Вечтомов

«___»___________2005 г. Декан факультета В.И. Варанкина

Киров 2005

Оглавление.

Введение …………………………………………………………………стр. 3

Глава 1 ……………………………………………………………………стр. 4

1.  Упорядоченные множества ………………………………………стр. 4

2.  Решётки.……………………………………………………………стр. 5

3.  Дистрибутивные решётки ………………………………………..стр. 8

4.  Топологические пространства……………………………………стр.10

Глава 2…………………………………………………………………….стр.11

1. Верхние полурешётки…………………………………………….стр.11

2. Стоуново пространство …………………………………………..стр.15

Список литературы……………………………………………………….стр.21

Введение.

Дистрибутивная решётка является одним из основных алгебраических объектов. В данной работе рассматривается частично упорядоченное множество P(L) простых идеалов. Оно даёт нам много информации о дистрибутивной решётке L, но оно не может её полностью охарактеризовать. Поэтому, для того, чтобы множество P(L) характеризовало решётку L, необходимо наделить его более сложной структурой. Стоун [1937] задал на множестве P(L) топологию.

В этой работе рассматривается этот метод в несколько более общем виде.

Работа состоит из двух глав. В первой главе вводятся начальные понятия, необходимые для изучения данной темы. Во второй главе рассматриваются верхние полурешётки, а также множество простых идеалов с введенной на нём топологией.

Глава 1.

1.  Упорядоченные множества.

Определение: Упорядоченным множеством  называется непустое множество, на котором определено бинарное отношение , удовлетворяющее для всех  следующим условиям:

1.Рефлексивность: .

2.Антисимметричность: если  и , то .

3.Транзитивность: если и , то .

Если  и , то говорят, что  меньше  или  больше , и пишут  или .

Примеры упорядоченных множеств:

1.  Множество целых положительных чисел, а  означает, что  делит .

2.  Множество всех действительных функций  на отрезке  и

 означает, что  для .

Определение: Цепью называется упорядоченное множество, на котором для  имеет место  или .

Используя отношение порядка, можно получить графическое представление любого конечного упорядоченного множества . Изобразим каждый элемент множества  в виде небольшого кружка, располагая  выше , если . Соединим  и  отрезком. Полученная фигура называется диаграммой упорядоченного множества .

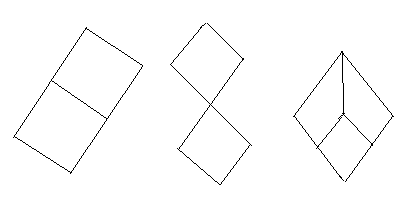
Примеры диаграмм упорядоченных множеств: