ПРЕОБРАЗОВАНИЕ РАДОНА

2. ПРЕОБРАЗОВАНИЕ РАДОНА

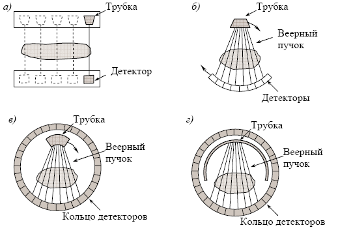
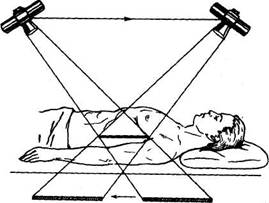
2.1 Рассмотрим задачу восстановления двумерного распределения коэффициента ослабления  при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол , и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение . Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.

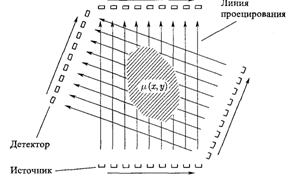
Рисунок 3. Схема кругового сканирования с параллельными проекциями.

Пусть на плоскости, где введена прямоугольная система координат  задана функция . Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим , зависит от того, по какой именно прямой проводится интегрирование.

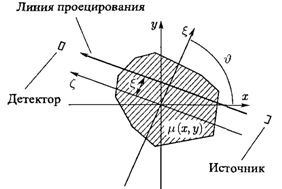
Рисунок 4. К выводу формул преобразования Радона.

Известно, что всякая прямая может быть описана уравнением

, (2.1)

где  - расстояние от начала координат до этой прямой;  - угол, образованный с осью  перпендикуляром, опущенным из начала координат на эту прямую.

Произвольная прямая  однозначно задается двумя параметрами  и . Поэтому и результат интегрирования функции  по некоторой прямой будет зависеть от этих же параметров, т.е. . Предположим, что функция  интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции  на плоскости  ставит в соответствие функцию  на множестве всех прямых, задаваемую интегралами от  вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию  часто называют образом функции  в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид

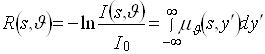. (2.2)

Задача ставится следующим образом: функция  неизвестна, но известна функция , являющаяся образом  в пространстве Радона; требуется по функции  определить . Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.

Согласно определению радоновского образа и с учетом того, что интеграл от заданной функции вдоль прямой равен интегралу по всей плоскости произведения этой функции на - функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]

. (2.3)

Интегрирование, осуществляемое по двум переменным, можно свести к интегрированию по одной переменной. Для этого введем еще одну прямоугольную систему координат , повернутую относительно  на угол . Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:

  (2.4)

  (2.5)

Сделаем в (2.3) замену переменных (2.4)

=

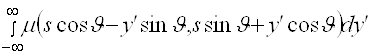= (2.6)

Для функции , отличной от нуля в пределах некоторой ограниченной области, ее радоновский образ также определяется выражением (2.3), только интегрирование проводится не по всей плоскости, а задается границами данной области. Так, если  отлична от нуля внутри круга радиуса , то вместо (2.6) имеем

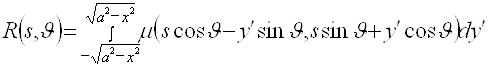. (2.7)

В общем случае функция, описывающая радоновский образ, обладает одним важным свойством

. (2.8)

Физический смысл этого свойства состоит в том, что любые пары  и  согласно (2.1) задают одну и ту же прямую.

Приведем примеры, которые иллюстрируют вычисление радоновских образов.

Пример 1.

Пусть . Подставим это выражение в (2.6) и получим (см. Приложение А)

=

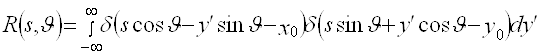=. (2.9)

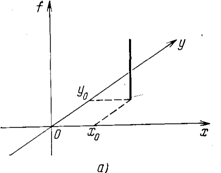
Из (2.9) следует, что если функция  отлична от нуля в точке , то функция, описывающая ее образ в пространстве Радона , отлична от нуля на линии

, (2.10)

 где .

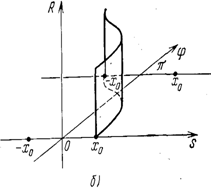
Рисунок 5. - функция (а) и ее радоновский образ (б)

 

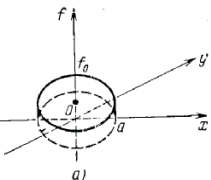
Пример 2.

Пусть 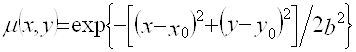. Подставляя это выражение в (2.6), получим

 . (2.11)

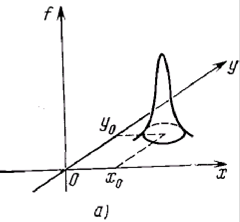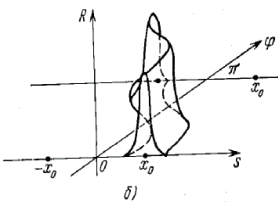
Рисунок 6. Функция (а) и ее радоновский образ (б)

Область, где  принимает максимальные значения, представляет собой линию, которая определяется выражением (2.10).

Пример 3.

При 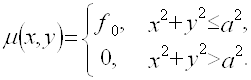 (2.12)

получаем

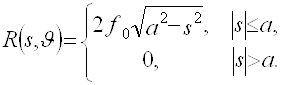 (2.13)

Рисунок 7. Функция (а) и ее радоновский образ (б)

2.2  В случае самоизлучающего объекта основной задачей ЭВТ является задача восстановления двумерного распределения источников излучения . Для простоты будем считать, что область, в которой распределены источники излучения, целиком расположена в области поглощения излучения, характеризующейся функцией распределения коэффициента ослабления . Обычно при измерениях с помощью ЭВТ, также как и при ТВТ, используют круговую схему с параллельными проекциями.

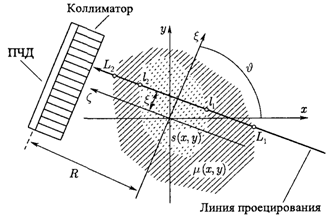
Рисунок 8. Круговая геометрия измерений в ЭВТ.

В [3] показано, что для ЭВТ с постоянным коэффициентом ослабления  экспоненциальное преобразование Радона в декартовых координатах имеет вид

, (2.14)

а в полярных координатах

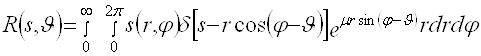. (2.15)

Выражение (2.15) можно переписать в другом виде

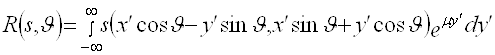. (2.16)

2.3 Выражения (2.3), (2.6) позволяет по функции  найти ее радоновский образ . Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть  - одномерное преобразование Фурье функции  по переменной , а  - двумерное преобразование Фурье функции  по переменным . Согласно определению

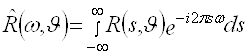, (2.17)

. (2.18)

В трехмерном пространстве введем прямоугольную систему координат, у которой по одной оси отложены значения , а по двум другим – значения  и .

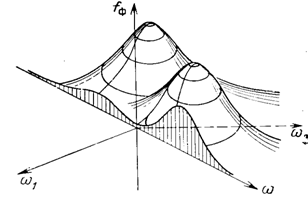
Рисунок 9. Центральное сечение двумерного преобразования Фурье

Проведем плоскость, перпендикулярную плоскости  и проходящую через начало координат, такую, что линия ее пересечения с плоскостью  составляет с осью  угол, равный  (центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции  получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно , координаты точки этой прямой в плоскости  равны  и . Следовательно,  подстановкой ,  превращается в .

Теорема.

Пусть функция  и ее радоновский образ  таковы, что существуют их преобразования Фурье. Тогда одномерное преобразование Фурье радоновского образа  по переменной  равно функции, описывающей центральное сечение двумерного преобразования Фурье, соответствующее тому значению , при котором вычисляется преобразование Фурье функции

. (2.19)

Для доказательства (2.19) подставим в (2.17) вместо  выражение (2.6) и сделаем замену переменных, аналогичную (2.4), полагая в (2.4) . Тогда получаем

=

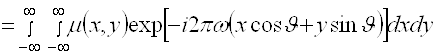. (2.20)

Сравнивая последний интеграл в (2.20) с (2.18), видим, что они равны, если в (2.20) под  и  понимать соответственно  и . Следовательно, последний интеграл в (2.20) равен , что и доказывает сформулированную теорему. Легко убедиться, что теорема о центральном сечении справедлива и для случая, когда верно равенство (2.7).

2.4 Рассмотрим теперь формулы обращения и алгоритмы реконструкции, основанные на теореме о центральном сечении. Известно, что по двумерному преобразованию Фурье можно найти :

. (2.21)

Сделаем в (2.21) замену переменных, перейдя в плоскости  к полярным координатам , так что , . Тогда (2.21) принимает вид:

. (2.22)

Теперь воспользуемся равенством (2.19) и вместо  подставим в (2.22) функцию , после чего получим

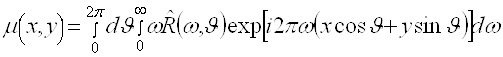 (2.23)

Равенство (2.23) и является искомой формулой обращения, позволяющей с учетом (2.17) по  найти функцию . Однако привлечение этого равенства для обработки данных томографических экспериментов оказывается не очень удобным из-за используемой в нем области интегрирования. Принимая во внимание равенство

, (2.24)

получим окончательное выражение для обращения преобразования Радона (см. Приложение Б)

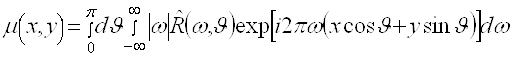. (2.25)

Для выявления детальной структуры алгоритма восстановления перепишем

(2.25) в несколько ином виде. Обозначим

 (2.26)

и введем функцию от  и  равную

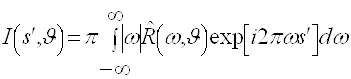. (2.27)

Тогда (2.25) принимает вид

, (2.28)

где при вычислении интеграла по  величина  должна быть заменена в соответствии с (2.26) на . В целом, алгоритм обращения преобразования Радона можно интерпретировать как последовательность операций:

1) для данного радоновского образа  определяется его преобразование Фурье ;

2) функция  умножается на ;

3) вычисляется обратное преобразование Фурье произведения  и тем самым определяется функция ;

4) аргументу  функции  присваивается значение (2.26);

5) проводится интегрирование функции  по углу .

Рассмотрим теперь иной вид формулы обращения по сравнению с (2.25). Обозначим через  импульсную реакцию фильтра с частотной характеристикой . Связь между этими функциями устанавливается прямым и обратным преобразованием Фурье

 (2.29)

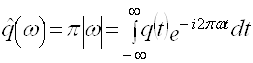 (2.30)

Заметим, что функция  обладает свойством .

Подставим в (2.25) вместо  правую часть (2.30), а вместо  - (2.17). Тогда получим

 (2.31)

Интегрирование по  дает , а последующее интегрирование по  приводит к выражению

 (2.32)

Выражение (2.32) отличается от (2.25) тем, что в последнем участвует преобразование Фурье радоновского образа, а в (2.32) сам радоновский образ. Алгоритм (2.32) можно представить как совокупность трех последовательных операций:

1) вычисляется свертка данного радоновского образа с функцией ;

2) аргументу  функции 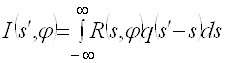, описывающей получаемую свертку, присваивается значение (2.26);

3) проводится интегрирование функции  по углу .

2.5 Обращение экспоненциального преобразования Радона (2.14) – (2.16) представляет существенно более сложную задачу. Ограничимся здесь рассмотрением только случая радиально-симметричной функции . Тогда экспоненциальное преобразование Радона  превращается в экспоненциальное преобразование Абеля  [2]

 ==.

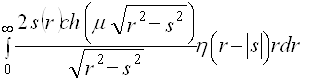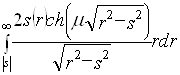В [2] показано, что обратное экспоненциальное преобразование Абеля имеет вид

 =

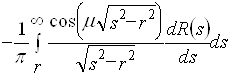. (2.33)