Методы составления начального опорного плана

3. Методы составления начального опорного плана.

 

Как и в общем случае, решение транспортной задачи начинается с отыскания первого опорного плана (исходного базиса). Мы рас­смотрим два наиболее распространенных метода построения такого базиса. Суть обоих этих методов состоит в том, что базисный план составляется последова­тельно, в несколько шагов (точнее,  шагов). На каждом из этих шагов заполняется одна клетка, притом так, что, либо пол­ностью удовлетворяется один из заказчиков (тот, в столбце кото­рого находится заполняемая клетка), либо полностью вывозится весь запас груза с одной из баз (с той, в строке которой находится заполняемая клетка).

-   В первом случае мы можем исключить столбец, содержащий заполненную на этом шаге клетку, и считать, что задача свелась к заполнению таблицы с числом столбцов, на единицу меньшим, чем было перед этим шагом, но с тем же количеством строк и с соот­ветственно измененным запасом груза на одной из баз (на той базе, которой был удовлетворен заказчик на данном шаге).

-   Во втором случае исключается строка, содержащая заполняемую клетку, и счи­тается, что таблица сузилась на одну строку при неизменном количестве столбцов и при соответствующем изменении потреб­ности заказчика, в столбце которого находится заполняемая клетка.

Начиная с первоначально данной таблицы и повторив  раз описанный шаг, мы придем к “таблице”, состоящей из одной строки и одного столбца (иначе говоря, из одной пустой клетки). Другими словами, мы пришли к задаче с одной базой и с одним потребителем, причем потребности этого единственного заказчика равны запасу груза на этой единственной базе. Заполнив последнюю клетку, мы освобождаем последнюю базу и удовлетворяем потреб­ность последнего заказчика. В результате, совершив  шагов, мы и получим искомый опорный план.

Замечание. Может случиться, что уже на некотором (но не на последнем!) шаге потребность очередного заказчика окажется рав­ной запасу груза на очередной базе. Тогда после заполнения оче­редной клетки объем таблицы как бы одновременно уменьшается на одни столбец и на одну строку. Но и при этом мы должны считать, что уменьшение объема таблицы происходит либо на один столбец, а на базе сохраняется “остаток” равный нулю, либо на одну строку, а у заказчика еще осталась неудовлетворенная “потребность” в количестве нуля единиц груза, которая и удовле­творяется на одном из следующих шагов. Этот нуль (“запас” или “потребностью” – безразлично) надо записать в очередную заполняе­мую клетку на одном из последующих шагов. Так как при этом оказывается равной нулю одна из базисных неизвестных, то мы имеем дело с вырожденным случаем.

Различие методов отыскания первого опорного плана состоит в различии способов набора заполняемой клетки.

1.Диагональный метод, или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) остав­шейся части таблицы. При таком методе заполнение таблицы начи­нается с клетки неизвестного  и заканчивается в клетке неизвест­ного , т. е. идет как бы по диагонали таблицы перевозок.

 

Пример.

 

Пункты Отправления	Пункты назначения										Запасы
		70		50		15		80		70	300
	170		110		20
		80		90		40		60		85	150
					80		70
		50		10		90		11		25	250
							50		200
Потребности	170		110		100		120		200		700

Заполнение таблицы начинается с ее северо-западного угла, т. е. клетки с неизвестным . Первая база  может полностью удовле­творить потребность первого заказчика  . Полагая , вписываем это значение в клетку  и исключаем из рассмотрения первый столбец. На базе  остается измененный запас . В оставшейся новой таблице с тремя строками  и четырьмя столбцами ; северо-западным углом будет клетка для неизвестного . Первая база с запасом может полностью удовлетворить потребность второго заказчика  . Полагаем , вписываем это значе­ние в клетку  и исключаем из рассмотрения второй столбец. На базе  остается новый остаток (запас) . В оставшейся новой таблице с тремя строками  и тремя столбцами  северо-западным углом будет клетка для неизвестного . Теперь третий заказчик  может принять весь запас с базы  . Полагаем , вписываем это значение в клетку  и исключаем из рассмотрения первую строку. У заказ­чика из  осталась еще не удовлетворенной потребность .

Теперь переходим к заполнению клетки для неизвестного  и т.д.

Через шесть шагов у нас останется одна база  с запасом груза (остатком от предыдущего шага) и один пункт  с потреб­ностью. Соответственно этому имеется одна свободная клетка, которую и заполняем, положив . План составлен. Базис образован неизвестными . Правиль­ность составленного плана легко проверить, подсчитав суммы чисел, стоящих в заполненных клетках по строкам и столбцам.

Общий объем перевозок в тонно-километрах для этого плана составит

.

2.Метод наименьшей стоимости. При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них.

 

Пример.

 

Пункты Отправления	Пункты назначения										Запасы
		70		50		15		80		70	300
	20				100				180
		80		90		40		60		85	150
	150
		50		10		90		11		25	250
			110				120		20
Потребности	170		110		100		120		200		700

В данном случае заполнение таблицы начинается с клетки для неизвест­ного , для которого мы имеем значение , наименьше из всех значений . Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе  и вто­рому заказчику . Третья база  может полностью удовлетворить потребность второго заказчика  . Пола­гая , вписываем это значение в клетку  и исключаем из рассмотрения второй столбец. На базе  остается изменённый запас . В оставшейся новой таблице с тремя строками  и четырьмя столбцами  клеткой с наименьшим значе­нием  клетка, где. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В резуль­тате оказываются заполненными (в приведенной последовательности) следующие клетки:

.

На пятом шаге клеток с наименьшими значениями  оказалось две . Мы заполнили клетку для , положив . Можно было выбрать для заполнения другую клетку, положив , что приведет в результате к другому опорному плану. Общий объем перевозок в тонно-километрах для этого плана составит

.

Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами (что и имеет место в нашем примере), хотя это и не обязательно.

Кроме рассмотренных выше способов иногда используется, так называемый, метод Фогеля. Суть его состоит в следующем: В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и ранее.

 

4.Понятие потенциала и цикла.

 

Для перехода от одного базиса к другому при решении транспортной задачи используются так называемые циклы.

Циклом пересчета или короче, циклом в таблице перевозок называется последовательность неизвестных, удовлетворяющая следующим условиям:

1.  Одно из неизвестных последовательности свободное, а все остальные – базисные.

2.  Каждые два соседних в последовательности неизвестных лежат либо в одном столбце, либо в одной строке.

3.  Три последовательных неизвестных не могут находиться в одном столбце или в одной строке.

4.  Если, начиная с какого-либо неизвестного, мы будем последовательно переходить от одного к следующему за ним неизвестному то, через несколько шагов мы вернемся к исходному неизвестному.

Второе условие означает, что у двух соседних неизвестных в цикле либо первые, либо вторые индексы одинаковы.

Если каждые два соседних неизвестных цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в свободной клетке, а остальные - в базисных клетках.

Можно доказать, что для любой свободной клетки таблицы перевозок существует один и только один цикл, содержащий свободное неизвестное из этой клетки, и что число вершин в цикле всегда четно.

Так, например, в таблице перевозок, составленной по диагональному методу при решения задачи из предыдущего пункта, неизвестному  соответствует цикл  и т.д.

Пусть теперь мы имеем некоторую свободную клетку с соответствующим ей циклом. Если мы изменим значение свободного неизвестного, увеличив его на некоторое число , то, переходя последовательно от одной вершины цикла к другой, мы должны будем в силу неизменности сумм по строкам и по столбцам поочередно уменьшать и увеличивать значения неизвестных в цикле на то же число. Например, в указанном выше цикле для свободного неизвестного  получим:

старые значения: ;

новые значения:

Очевидно, если снабдить вершины цикла поочередно знаками “+” и “–“, приписав вершине в свободной клетке знак “+”, то можно сказать, что в вершинах со знаком “+” число  прибавляется к прежнему значению неизвестного, находящегося в этой вершине, а в вершинах со знаком “–“ это число  вычитается из прежнего значения неизвестного, находящегося в этой вершине.

Замечание. Так как число вершин в цикле всегда четно, то, возвращаясь в свободную клетку, мы должны будем приписать ей знак “+”, т. е. тот знак, который ей уже приписан при выходе из нее. Это очень существенное обстоятельство, так как иначе мы пришли бы к противоречию. Безразлично также, в каком направлении обходится цикл при “означивании” вершин.

Если в качестве  выбрать наименьшее из чисел, стоящих в вершинах, снабженных знаком “–“, то, по крайней мере, одно из прежних базисных неизвестных примет значение нуль, и мы можем перевести его в число свободных неизвестных, сделав вместо него базисным то неизвестное, которое было свободным.

Так, например, в рассмотренном выше цикле имеем отрицательные вершины  и ; следовательно, выбрав , мы получаем:

старые значения: ;

новые значения:

т. е. вместо прежнего базисного решения получаем новое базисное решение:

Пункты Отправления	Пункты назначения										Запасы
		70		50		15		80		70	300
	90		110		100
		80		90		40		60		85	150
	80						70
		50		10		90		11		25	250
							50		200
Потребности	170		110		100		120		200		700

Выбор в качестве х минимального среди чисел, стоящих в отрицательных вершинах цикла, обеспечивает допустимость нового базиса.

Если минимальное значение среди базисных неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной отрицательной вершине, то свободной оставляют только одну из них, а в других клетках с тем же минимальным значением пишут нули. В этом случае новое базисное решение будет вырожденным.

Может случиться, что и само минимальное значение среди чисел в отрицательных клетках равно нулю. Тогда преобразование таб­лицы перевозок сведется к перестановке этого нуля в свободную клетку. Значения всех неизвестных при этом остаются неизменными, но решения считаются различными, так как различны базисы. Оба решения вырождены.

Описанное выше преобразование таблицы перевозок, в результате которого преобразуется базис, называется пересчетом по циклу.

Заметим, что неизвестные, не входящие в цикл, этим преобразованием не затрагиваются, их значения остаются неизменными и каж­дое из них остается либо в группе базисных, либо в группе свобод­ных неизвестных, как и до пересчета.

Выясним теперь, как пересчет по циклу влияет на общий объем затрат на перевозки и при каком условии эти затраты становятся меньше.

Пусть  – некоторое свободное неизвестное, для которого мы построили цикл и осуществили пересчет по циклу с некоторым числом . Если вершине цикла, находящейся в  строке и  столбце таблицы перевозок, приписан знак “+”, то значение неизвестного , находящегося в этой вершине, увеличивается на , что в свою очередь вызывает увеличение затрат на . где  – тариф, соответствующий этой клетке; если же указанной вершине приписан знак “–”, то значение неизвестного  уменьшается на , что вызывает уменьшение затрат на .

Сложим тарифы, соответствующие положительным вершинам цикла, и вычтем из этой суммы сумму тарифов, соответствующих отрицательным вершинам цикла; полученную разность  назовем алгебраической суммой тарифов для данного свободного неизвестного . Подсчет алгебраической суммы тарифов можно истолковать и так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком (“относительных тарифов”).

Теперь, очевидно, мы можем, заключить, что в целом при пере­счете но циклу, соответствующему свободному неизвестному  общий объем затрат на перевозки изменится на произведение алгеб­раической суммы тарифов на , т. е. на величину . Следовательно, если алгебраическая сумма тарифов для некоторого свобод­ного неизвестного  отрицательна , то пересчет по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же алгебраическая сумма тарифов положительна , то пересчет по соответствующему циклу приведет к увеличению общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю , то пересчет по соответствующему циклу не изменит общую сумму затрат (два различных базисных плана требуют одинаковых затрат на их реализацию).

Так, например, для цикла  в рассмотренной задаче алгебраическая сумма тарифов

.

Значит, пересчет по этому циклу снижает расходы. И действитель­но, осуществив такой пересчет, мы получаем план, по которому объем перевозок в тонно-километрах составляет

тогда как по исходному плану он составил . Имеем снижение объема перевозок на 1200 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в дан­ном случае равна –15, а пересчет по циклу осуществляется с помощью числа  (изменение затрат равно ).

Вычисление алгебраической суммы тарифов для каждого из сво­бодных неизвестных можно производить без построения соответ­ствующего цикла, пользуясь, так называемыми, потенциалами. При­пишем каждой базе , некоторое число  и каждому потребителю  некоторое число :

,

так что

(4.1)

,

где  – тарифы, соответствующие клеткам, заполненным базис­ными неизвестными. Эти числа  и  называются потенциалами соответствующих баз и потребителей.

Зная потенциалы, легко вычислить алгебраическую сумму тари­фов. Действительно, если в алгебраической сумме тарифов по циклу, соответствующему свободному неизвестному , заменить тарифы базисных клеток их выражениями через потенциалы по формулам (4.1), то, в силу чередования знаков при вершинах цикла, все потенциалы, кроме  и  сократятся, и мы получим:

.

Так, например, для цикла  в рассмотренной выше задаче имеем

.

Для базисных клеток сумма потенциалов строки и столбца, в которых находится эта клетка, равна тарифу, соответствующему этой клетке; если же клетка для неизвестного  свободная, то сумму потенциалов

(4.2)

называют косвенным тарифом этой клетки. Следовательно, алгеб­раическая сумма тарифов для свободной клетки  равна разности ее настоящего (“истинного”) и косвенного тарифов:

(4.3)

Из (4.3) следует, что если косвенный тариф для данной свобод­ной клетки больше её истинного тарифа, то алгебраическая сумма тарифов по циклу, соответствующему этой клетке, будет отрица­тельна; если же косвенный тариф меньше истинного, то алгебраи­ческая сумма тарифов положительна, и, наконец, если косвенный тариф равен истинному, то алгебраическая сумма тарифов равна нулю.

Потенциалы можно найти из системы равенств (4.1), рассматри­вая их как систему  уравнений с  неизвестными. Так как неизвестных здесь на единицу больше, чем уравнений, то, по крайней мере, один из потенциалов мы можем выбрать произвольно, положив, например, ; тогда остальные потенциалы легко опре­деляются из уравнений (4.1).

Например, для плана, полученного по диагональному методу в рассмотренной выше задаче, имеем

Система содержит семь уравнений с восемью неизвестными. Выбирая произвольно значение , находим последовательно из пер­вых трех уравнений значения , , , затем из четвертого уравнения – , из пятого уравнения – , из шестого уравнения  и, наконец, из седь­мого уравнения – .

Положив, например, , получаем значения потенциалов:

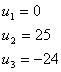
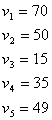
Найдем теперь косвенные тарифы для свободных клеток и сравним их с истинными тарифами:

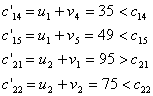
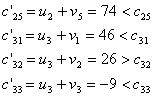
Для клеток с неизвестными  и  косвенные тарифы больше истинных. Следовательно, для них мы будем иметь отрицательные алгебраические суммы тарифов:

Значение  мы уже имели раньше, вычисляя алгебраиче­скую сумму тарифов для этой клетки непосредственно по циклу.

Замечание 1. Подсчитывая косвенные тарифы как суммы соответ­ствующих потенциалов, полезно не пропускать и клетки с базисны­ми неизвестными (заполненные клетки). Для этих клеток сумма потенциалов равна истинному тарифу; последнее может служить проверкой правильности найденных значении потенциалов.

Замечание 2. Можно показать, что если сумму всех затрат по данному плану перевозок выразить через свободные неизвестные [для этого надо исключить базисные неизвестные из выражения для S, см. формулу (2.4)], то коэффициент при каждом из таких неизвестных будет равен алгебраической сумме тарифов по циклу, соответствующему ей в таблице перевозок. Это еще раз подтверждает, что пересчет по циклам является специфической формой применения симплекс-метода к решению транспортной задачи.