Доведення ірраціональності та трансцендентності числа „π”

1.3 Доведення ірраціональності та трансцендентності числа „π”

Доведемо ірраціональність і транcцендентність числа .

Теорема 1.3.1.Число  ірраціональне.

Доведення. Припустимо, що  раціонально, тобто , де  й  натуральні числа. При збільшенні  величина 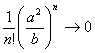; тому можна знайти  таке . що виконується нерівність

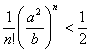(1.3.1)

Розглянемо для такого  функцію

(1.3.2)

Заміняючи  через  і розкладаючи  по ступенях  , можна представити  у вигляді:

(1.3.3)

так що . Якщо рівність 1.3.3 продифференціювати  разів, де , то одержимо:

Біноміальний коэфициент  ціле число, так що  цілі числа.

З рівності 1.3.2 видно, що , так що диференцируючи, одержуємо для всіх

, і отже,

, цілі числа.

Інтегруючи  вроздріб, одержуємо:

 (1.3.4)

тому що наступна похідна  тотожно дорівнює нулю.

З рівності (1.3.4) одержуємо:

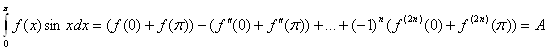 (1.3.5)

де ціле число.

Оскільки в інтервалі  подінтегральна функція  позитивна, то інтеграл у лівій частині (1.3.5) більше нуля й . З іншого боку, з рівності (1.3.2) видно, що при  маємо:

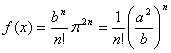
і оскільки  , то при нашім виборі  маємо:

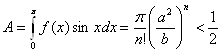
тобто .

Припущення, що  раціонально, привело нас до протиріччя, отже , ірраціональне.

Теорема доведена.

Ірраціональність числа була доведена вперше в 1761 році французьким математиком Ламбертом. Доказ Ламберта заснований на застосуванні безперервних дробів.

π — трансцендентне число, це означає, що воно не може бути коренем багаточлена із цілими коефіцієнтами. Трансцендентність числа π була доведена в 1882 році професором Кьонінгзбергського, а пізніше Мюнхенського університету Ліндеманом. Доказ спростив Феликс Клейн в 1894 році.

Для того щоб довести трансцендентність числа π доведемо спочатку три допоміжних твердження.

Лема 1.3.1. При будьякому цілому позитивному  й будьякому , має місце рівність

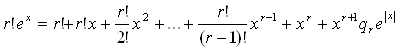 (1.3.6)

де

Доведення. Скористаємося розкладанням функції  в ряд

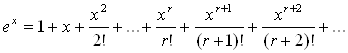
Із цього розкладання треба, щоб

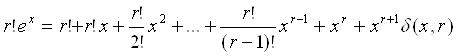
де

Тому що

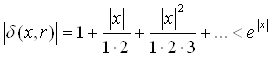
Лема доведена.

Лема 1.3.2 Нехай

 

де

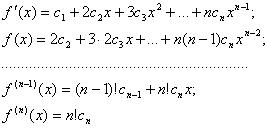
Тоді

 

(1.3.7)

де

(1.3.8)

(1.3.9)

Покладаючи в рівності (1.3.6) , одержимо

 

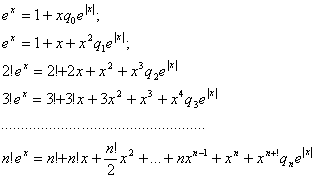
Помноживши ці рівності, відповідно, на  й склавши, одержимо рівність (1.3.7).

Лема 1.3.3. Сума й добуток двох алгебраїчних чисел є числами алгебраїчними (і притім цілими алгебраїчними, якщо такими є доданки й множники).

Доведення. Дійсно нехай алгебраїчне число, що є коренем рівняння ого ступеня з раціональними коефіцієнтами  й інших корінів цього рівняння й нехай – алгебраїчне число , що є коренем рівняння ой ступеня з раціональними коефіцієнтами , а  – інших корінів цього рівняння.

Добуток всіх різниць виду, мабуть, є багаточленом, одним з корінів якого є . Отже, нам досить переконатися в тім, що коефіцієнти цього багаточлена суть раціональні числа. Але ці коефіцієнти суть симетричні функції від аргументів і аргументів . Застосовуючи двічі теорему про симетрію функції (“Якщо симетрична функція  є багаточленом і корінь рівняння  те  де  багаточлен. Зокрема, якщо коефіцієнти багаточлена  цілі числа , то коефіцієнти багаточлена  теж цілі числа ” [9], ми переконаємося в справедливості нашого твердження про добуток алгебраїчних чисел. Аналогічно доводиться твердження про суму

Тепер перейдемо до доказу самої теореми, що  транcцендентне число.

Теорема. транcцендентне число.

Доведення. Нехай  алгебраїчне число . На підставі леми 1.3.3 число теж алгебраїчне й отже, є корнем рівняння виду

(1.3.10)

з цілими коефіцієнтами. Нехай  корінь цього рівняння , одним з них є . Тому що , то

 

(1.3.11)

Розкривши дужки в лівій частині цієї рівності , одержимо

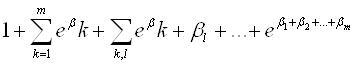 (1.3.12)

Позначимо через  ті з показників, які відмінні від нуля , а через  інші. Приєднавши відповідні доданки в лівій частині (1.3.12) до першого, можемо записати рівність (1.3.12) у вигляді

 

(1.3.13)

де ціле позитивне число.

Числа  суть цілі алгебраїчні числа, тому згідно лемі (1.3.3) цілими алгебраїчними числами є й числа

Дуже важливо помітити , що якщо  симетричний багаточлен із цілими коефіцієнтами , те  ціле число

Дійсно, якщо

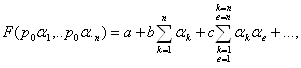
то буде також

тому що кожна із сум, що коштують у правій частині другої рівності, відрізняється від відповідної суми першої рівності, що складаються або рівними  або утримуючого цього числа як множники, а числа  дорівнюють нулю.

Вираз в правій частині останньої рівності є симетричним багаточленом відносно  й отже , відносно . На підставі теореми [20]: “Якщо  симетричний багаточлен із цілими коефіцієнтами й  корінь уранения  із цілими коефіцієнтами, тj  ціле число ” , треба, щоб  було цілим числом.

Покладемо в рівності (1.3.7) , послідовно ,  і складемо результати , помноживши попередньо перші з них на .Одержимо на підставі (1.3.13)

 (1.3.14)

Якщо ми доведемо, що для деякого багаточлена  рівність (1.3.14) неможлива, якщо  алгебраїчні числа, то тим самим буде доведена трансцендентність .

Покладемо

(1.3.15)

де просте число, що залишається поки невизначеним. Багаточлен (1.3.15) можна представити у видах

 

(1.3.16)

Перше з рівностей (1.3.16) безпосередньо отримане з рівності (1.3.15), якщо в правій його частині розкрити дужки. При цьому одержимо

Добуток у правій частині симетричний й тому  ціле число. Такі ж, легко зміркувати є й числа .

Друге з рівностей (1.3.16) виходить із рівності (1.3.15) якщо записати його у вигляді

і звільнитися від квадратних дужок. Аналогічно виходить третє з рівностей (1.3.16) і так далі. Важливо помітити, що …є багаточленами із цілими коефіцієнтами відносно

Легко підрахувати, що

(1.3.17)

(1.3.18)

Сума

є симетричним багаточленом із цілими коефіцієнтами й тому є цілим числом. Це число, через (1.3.13) , ділиться на .

Ми будемо вважати  більшим кожного із цілих чисел . Тоді

буде цілим числом, яке не ділится на , тому що таким буде перший доданок у правій частині, у той час, як інші доданки будуть цілими числами, що діляться на . Таким чином, сума, що визначена в першій частині рівності (1.3.14), при нашому виборі числа , є цілим числом, що не ділиться на , тобто є відмінним від нуля цілим числом.

Повернемося до розгляду суми

З рівності (1.3.9) , першої рівності (1.3.16) і того , що

легко доглянути, що  буде по модулі меншим одиниці, при досить великому .

Таким чином, права частина рівності (1.3.14) є сумою цілого, відмінного від нуля, числа й числа, по модулі меншого одиниці. Така сума не може рівнятися нулю й тому рівності (1.3.14), при нашім виборі  й , неможливі. Цим і завершений доказ трансцендентності числа .

Теорема доведена.