Навигация
Содержание
Введение. 2
1. Характеры.. 3
1.1 Определение характера. Основные свойства характеров. 3
1.2 Суммы характеров. Соотношение ортогональности. 6
1.3 Характеры Дирихле. 8
2. L-функция Дирихле. 13
3. Доказательство теоремы Дирихле. 29
Введение
Простые числа расположены в натуральном ряде весьма неравномерно.
Целью данной работы является доказательство следующей теоремы о простых числах в арифметической прогрессии.
Теорема Дирихле. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.
Пусть
mn + l, n=1,2, …,
прогрессия, удовлетворяющая условию теоремы.
Условие (m, l)=1, наложенные на числа m и e в формулировке теоремы, естественно, поскольку в случае, когда d=(m, l)>1, все члены прогрессии делятся на d и поэтому не являются простыми числами.
Сформулированная теория была впервые высказана Л. Эйлером в 1783 г. В 1798 г. А. Лежандр опубликовал доказательство для четных m, использовавшее, как выяснилось позднее, одну ошибочную лемму.
Полностью доказал теорему в 1837–1839 гг. Петер Густав Лежен-Дирихле (1805–1859), немецкий математик, автор трудов по аналитической теории чисел, теории функций, математической физике.
В 1837 г. вышли две работы Дирихле, посвященные теореме о простых числах в арифметической прогрессии. Они содержали формулировку теоремы в общем виде, однако доказательство приводилось только для случая, когда разность прогрессии есть простое число. В конце второй работы содержится построение характеров для произвольного модуля и некоторые утверждения о том, как можно доказать утверждение L (1,χ)¹0 для неглавных характеров x в одном случае. В 1839 г. Дилихле опубликовал полное доказательство теоремы о простых числах в арифметической прогрессии. С тех пор она носит его имя.
1. Характеры 1.1 Определение характера. Основные свойства характеров
![]()
![]() Характером (от греческого хараæτήp-признак, особенность) χ конечной абелевой группы G называется не равная тождественно нулю комплекснозначная функция, определенная на этой группе и обладающая тем свойством, что если, АÎG и BÎG
Характером (от греческого хараæτήp-признак, особенность) χ конечной абелевой группы G называется не равная тождественно нулю комплекснозначная функция, определенная на этой группе и обладающая тем свойством, что если, АÎG и BÎG
χ (АВ)= χ (А) χ(В).
Обозначим через Е единичные элементы в группе G и через А-1 обратный элемент для АÎG
Характеры группы G обладают следующими свойствами:
1. Если Е-единица группы, то для каждого характера χ
χ (Е)=1 (1.1)
Доказательство. Пусть для каждого элемента АÎG справедливо неравенство
c1(А)=c(АЕ)= c(А) χ (Е)
Из этого равенства получим, что c (Е)¹0. Теперь из равенства
c (Е)= c (ЕЕ)= c (Е) c (Е)=1
следует равенство (1.1)
2. c (А) ¹0 для каждого АÎG
Действительно, если бы χ (А) =0 для некоторого АÎG, то
c (А) χ (А-1)= c (АА-1)= χ (Е)=0,
а это противоречит свойству 1.
3. Если группа G имеет порядок h, то Аh=Е для каждого элемента АÎG Следовательно,
1= χ (Е)= χ (Аh)= χ (А)h,
то есть χ (А) есть некоторый корень степени h из единицы.
Характер χ1, обладающий свойством χ1(А)=1 для каждого элемента АÎG, называется главным характером группы G. Остальные характеры называются неглавными.
Лемма 1. Пусть Н подгруппа конечной абелевой группы G, причем G/H – циклическая порядка n, тогда для каждого характера χH– подгруппы Н существует ровно n характеров.
Доказательство. Рассмотрим группу G=![]() gkH, причем gnH=H, gnÎH и gn=h1=1.
gkH, причем gnH=H, gnÎH и gn=h1=1.
Для каждого элемента XÎG существует и притом единственное к=кх и hх=h такое, что если 0£ кх <n, то X= gkх hх=gkh. Возьмем еще один элемент группы G, Y= gmhy, где 0£ m<n. Перемножим эти два элемента
ХY= gк+mhhy.
Определим характер χ (X).
χ (X)= χ (gк h)= χ (gк) χ (n)= χ к (g) χH (h).
В данном выражении неизвестным является χ (g).
χn(g)= χ (gn)= χ (h1)= χH(h1) – данное число.
![]() χ (g)= – n корней из 1,
χ (g)= – n корней из 1,
то есть ξјn=χn(g)= χH(h1), получаем xk(g)= ξјn. Следовательно, x(g)= ξ1, …, ξn
Из полученных равенств получаем:
χ (X)= χk(g) χH(hx)= ξjkxχH (hx)
χ (Y)= χm(g) χH(hy)= ξjkyχH (hy)
Определим умножение характеров
χ (X) χ (Y)= ξjkyχH (hy) ξjk-xχH (hx)= ξjkx+kyχH (hx) χH (hy)= jk+mχH (hhy)
Для того чтобы определение выполнялось, необходимо рассмотреть степень gkx+kx. Возможны два случая:
1) Если 0£ кх + ky<n, то
кх + ky= kxy,; hxhy= hxy.
В этом случае определение выполняется.
2) Если n£ кх + ky<2n-1, то получим
кх + ky = n + kxy..
Тогда
XY= g kx+ky hxhy=ghgkx+ky-n hx hy=gkx+ky-nh1hxhy
В свою очередь 0£ кх + ky – n£n-1 Þ kx+ky – n=kxy, h1hxhy= hxy.
χ (XY) = ξjkх+kу χн (hxу) = ξjkх + kу – nχн (h1) χн(hx) χн (hy) = ξjкх ξj ку ξj– n χн (h1) χн(hx) χн (hy) = ξj кх χн (h1х) · ξj ку χн(hy) = χ (X) χ(Y).
Лемма доказана.
Похожие работы
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... на ak может быть не более чем ak - 1 (ведь ни одно число не даёт остаток rk), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа M + sd и M + td (0 Ј s Ј ak - 1 и 0 Ј t Ј ak - 1). Тогда их разность (M + sd) - (M + td) = (s - t)d делится на ak, что невозможно, т.к. 0 < |s - t| < ak и d = a1a2...ak - 1 взаимно просто с ak, ибо числа a1, a2, . . ., ak ...
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
... рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение =, , , , , … 0,3; 0,42; 0,45; 0,467; … Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида. Например, имеется разложение =, , , , , , , … 1; 1,5; 1,38; 1,44; 1,40; … Но самое интересное и важное это то, что в то время как до настоящего ...
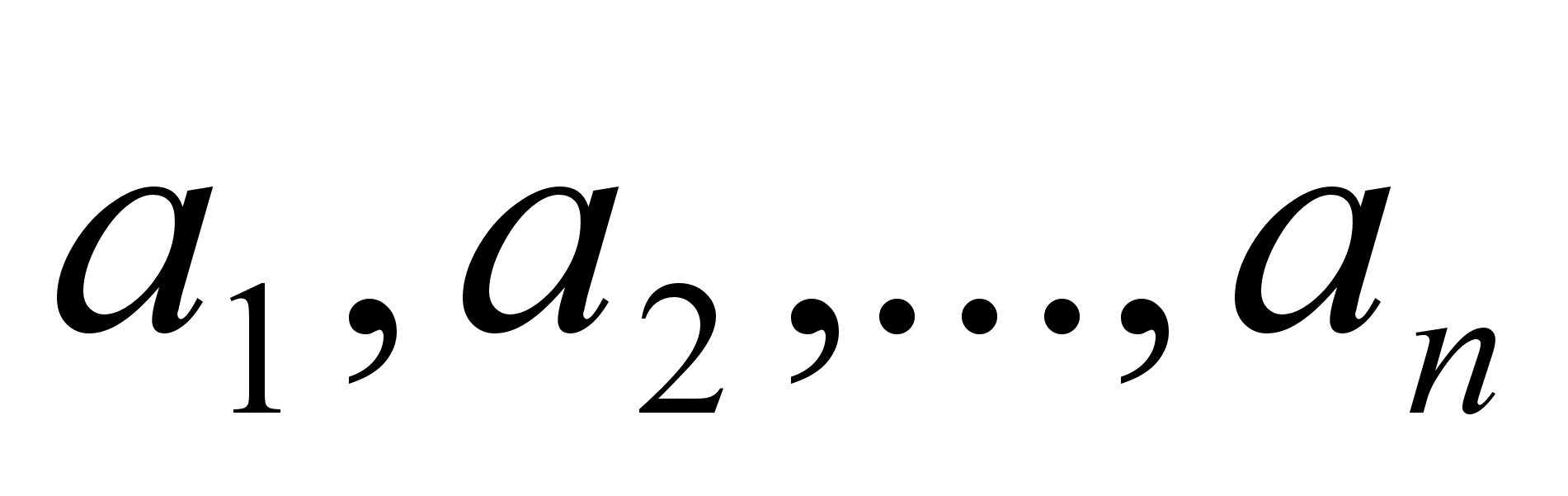
0 комментариев