Навигация
Рассмотрим c – вещественный характер, т.е. принимающий только вещественные значения, несовпадающий с главным характером
2. Рассмотрим c – вещественный характер, т.е. принимающий только вещественные значения, несовпадающий с главным характером
Лемма 8. Пусть c – вещественный характер.
Рассмотрим функцию
F(S) = ξ(S) L (S, x) (2.15)
Докажем, что если Re S>1, то
![]() (2.16)
(2.16)
представляется рядом Дирихле, которого справедливы следующие утверждения:
1) Все коэффициенты аn≥ 0
2) при n=k2, k ? / N(N)/ аn≥1
3) В области ReS<1 можно почленно дифференцировать, то есть
F (k) (S)= ![]() (-1)k(ln n)k
(-1)k(ln n)k![]() k=1,2…; (2.17)
k=1,2…; (2.17)
4) Ряд (1) в точке S=1/2 расходится.
Доказательство. В области ReS > 1 ряды, определяющие функции S(S) и L (S,c), абсолютно сходятся, поэтому их можно перемножить:
где
![]() (2.19)
(2.19)
Пусть ![]() - расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид
- расположение числа n в произведение простых сомножителей. Тогда все натуральные делители l числа n имеют вид
![]()
![]()
поэтому из равенства (14) находим, что
![]()
где ani = 1+ c (pi)+ … +cLi (pi), i=1,…, m (2.21)
так как c – вещественный характер, то он может принимать только три значения: 0, 1, -1. Из равенства (2.21) следует, что
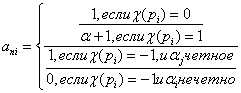 (2.22)
(2.22)
Во всех случаях числа ani³0, а значит, и an=an1 … anm³0
Если же число п является полным квадратом, то
N=k2=p/2g … pm2g,
и из равенств (2.20) и (2.22) следует, что аn ³1
При любом s > 0 в области ReS> 1 +s выполняется неравенство
![]()
Ряд (2.18) сходится в области ReS > 1. Поэтому по признаку Вейерштрасса ряд (2.16) сходится равномерно в области ReS > 1 + s, а по теореме Вейерштрасса его можно в этой области почленно дифференцировать любое число раз. Следовательно, в области ReS > 1 +s выполняется равенство (2. 17), а в силу произвольности s оно выполняется и в области ReS > 1.
Однако ряд (39) расходится, так как по второму утверждению леммы
Ряд (2.16) при S = ![]() имеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд
имеет неотрицательные члены. Поэтому, если бы он сходился, то также сходился бы ряд
![]() (2.23)
(2.23)
Следовательно, ряд (2.23) расходится. Лемма доказана.
Переходим непоредственно к доказательству второго случая теоремы. Допустим, что L (1,c) = 0. Тогда полюс дзета-функции будет компенсироваться в произведении S(S) L (S, c) нулем функции L (S, c).
Поэтому функция (2.15) F(S) будет аналитической в области ReS > 0 так как в точке S=1 у F(z) – устраненная особая точка. Следовательно, ее можно разложить в ряд Тейлора в точке S = 2:
![]() (2. 24)
(2. 24)
радиус сходимости которого не меньше 2 R³2/
Из равенств (2.17), в частности S=2, находим
![]() (2.25)
(2.25)
В радиусе сходимости будет брать не все S, а только вещественные ReS=s S=sÎ(0,2). Пользуясь разложениями (18) и (19), находим
![]()
Члены двойного ряда неотрицательны, поэтому он сходится абсолютно, и в нем можно поменять порядок суммирования. Тогда
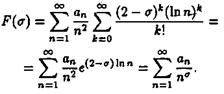
Следовательно, ряд (2.16) сходится во всех точках, s < (, 0, 2), и в точке ![]() , а это противоречит четвертому утверждению леммы. Поэтому L (S,c)¹0/
, а это противоречит четвертому утверждению леммы. Поэтому L (S,c)¹0/
Этим завершается доказательство теоремы
По следствию 2 леммы 2 функция ![]() является аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).
является аналитической в области ReS > 1. Для дальнейшего доказательства теоремы Дирихле нам будет необходимо представление этой функции в виде ряда, аналогичного ряда (2.16).
Лемма. Для каждого характера c(n) в области ReS > 1 справедливо равенство
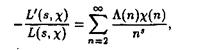 (2.26)
(2.26)

Доказательство.
Так как S=s+it имеет место неравенство
![]()
получаем, что ряд стоящий в правой части равенства (2.26), абсолютно сходится в области s>1. Умножим этот ряд на ряд определяющий L (S, c). Получили
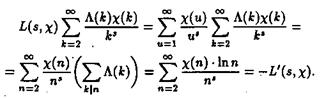
Предпоследнее равенство имеет место ввиду равенства ![]() ), а последнее – по следствию из леммы 3, равенство 2.7.
), а последнее – по следствию из леммы 3, равенство 2.7.
3. Доказательство теоремы Дирихле
Теорема. Если разность и первый член арифметической прогрессии есть взаимно простые натуральные числа, то она содержит бесконечное множество простых чисел.
Доказательство.
Рассмотрим равенство (2.26), которое справедливое по Лемме в области ReS > 1. Поскольку ![]() (n) = 0 для всех n, не являющихся степенями простых чисел, то все отличные от нуля члены ряда в правой части (2.26) имеют вид
(n) = 0 для всех n, не являющихся степенями простых чисел, то все отличные от нуля члены ряда в правой части (2.26) имеют вид
![]()
где р – простое и k – натуральное числа. Ряд (2.26) абсолютно сходится, следовательно, его можно представить в виде двойного ряда) и, значит, в области ReS > 1
![]() (3.1)
(3.1)
Второе слагаемое в правой части этого равенства равномерно ограничено по s в области ReS³3/4. Действительно, если S=p+it, p³3/4, то
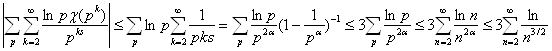
Следовательно, при S®1+0 для каждого характера c имеет место равенство
![]() (3.2)
(3.2)
Здесь и в дальнейшем s ® 1 + o обозначает, что S стремится к 1 по действительной оси справа.
Пусть u – некоторое натуральное число, удовлетворяющее сравнению
![]() (3.3)
(3.3)
Умножим обе части равенства (3.2) на c(u) и просуммируем получившиеся равенства по всем числовым характерам c. Тогда получим
![]() (3.3)
(3.3)
Если простое число р удовлетворяет сравнению р ºl (mod m), то pu ≠ 1 (mod m), и по теореме 1
![]()
Если же p≠l (mod m), то pu≠ 1 и по той же теореме
![]()
Таким образом, равенство (3.3) можно переписать в виде
![]() (3.4)
(3.4)
По лемме 3 и теореме 2 для неглавного характера c функция ![]() является аналитической в точке S = 1. Поэтому для таких характеров при S ®1 + 0 имеем
является аналитической в точке S = 1. Поэтому для таких характеров при S ®1 + 0 имеем
![]() (3.5)
(3.5)
По следствию 1 леммы 4 функция L (S, c1) имеет в точке S=1 полюс первого порядка. Значит, при S®1+0
![]() (3/6)
(3/6)
Учитывая равенства (3.5) и (3.6.) из равенства (26) получаем, что
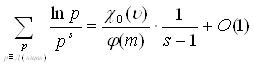
Так как число u удовлетворяет сравнению (3.3), то (u, m) = 1 и c0(u)=1. Итак, при S®1+0
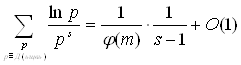 (3.7)
(3.7)
Правая часть равенства а (3.7) при S®1+0 имеет бесконечный предел. Значит, сумма, стоящая в левой части этого равенства, имеет бесконечное множество слагаемых. Поэтому существует бесконечное множество простых чисел, удовлетворяющих сравнению
pºe (mod m)
Теорема Дирихле доказана.
Похожие работы
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... на ak может быть не более чем ak - 1 (ведь ни одно число не даёт остаток rk), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа M + sd и M + td (0 Ј s Ј ak - 1 и 0 Ј t Ј ak - 1). Тогда их разность (M + sd) - (M + td) = (s - t)d делится на ak, что невозможно, т.к. 0 < |s - t| < ak и d = a1a2...ak - 1 взаимно просто с ak, ибо числа a1, a2, . . ., ak ...
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
... рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение =, , , , , … 0,3; 0,42; 0,45; 0,467; … Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида. Например, имеется разложение =, , , , , , , … 1; 1,5; 1,38; 1,44; 1,40; … Но самое интересное и важное это то, что в то время как до настоящего ...
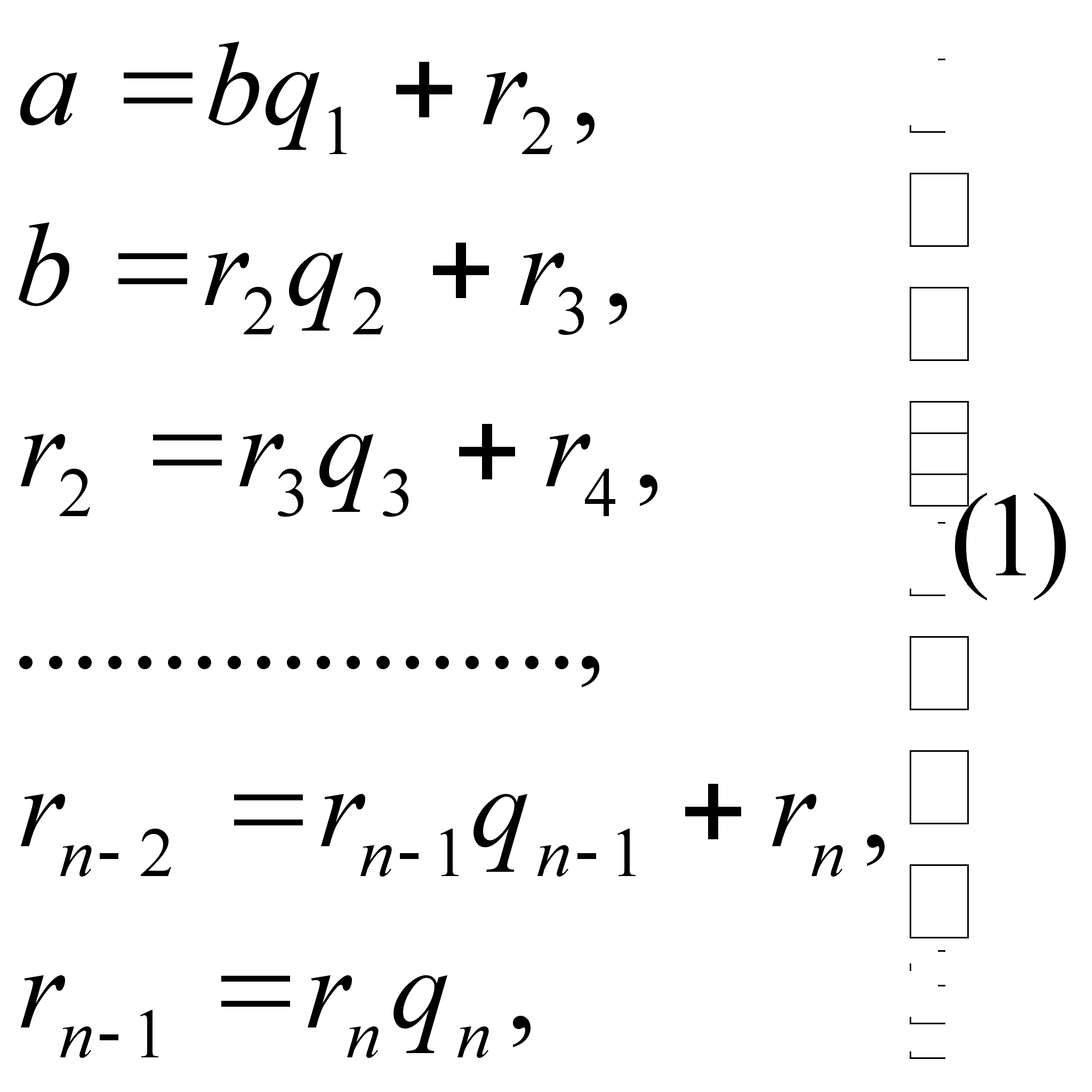
0 комментариев