Навигация
Характеры конечной мультипликативной абелевой группы G образуют конечную мультипликативную абелевую группу Ĝ
5. Характеры конечной мультипликативной абелевой группы G образуют конечную мультипликативную абелевую группу Ĝ.
Под произведением двух характеров χ' и х χ'' группы G будем понимать характер х, определяемый следующим свойством:
χ (AB) = χ' (A) χ'' (В)
Для любого элемента АÎG, имеем:
χ (АВ) = χ' (АВ) χ'' (АВ) = χ' (А) χ' (В) · χ'' (А) χ'' (В) = χ(А) χ(В)
Таким образом, получаем χ ' χ '' действительно является характером.
Роль единичного элемента группы G играет главный характер χ1
Обратным элементом G является:
![]() χ2 (g1 g2) =
χ2 (g1 g2) = ![]() =
=![]()
![]() =
= ![]() = χ2(g1) χ2(g1)
= χ2(g1) χ2(g1)
Пусть G – конечная мультипликативная абелева группа порядка h. Рассмотрим сумму:
S = ![]() ,
,
где А пробегает все элементы G, и сумму
Т = ![]()
где c пробегает все элементы группы характеров Ĝ.
Рассмотрим чему равна каждая из сумм.
а) Если В-фиксированный элемент группы G и А пробегает все элементы G, то АВ также пробегает все элементы группы G. Следовательно,
S·c (В) = ![]() c (В) =
c (В) = ![]() =
= ![]() = S.
= S.
Получили Sc (В) = S, откуда следует, что (c (В) – 1)·S = 0. Следовательно, возможны два варианта:
1) S = 0, то c (В) – негативный характер
2) S≠0, то c (В) = 1 для каждого элемента В?G и в этом случае c (В)= c1(В) есть главный характер и сумма S равна порядку h группы G. Таким образом,
S = ![]() = {
= {![]() (1.2)
(1.2)
б) Если мы умножим сумму Т на некоторый характер c’ группы Ĝ, то аналогичным образом получим
c’ (А) Т = ![]() c’ (А) =
c’ (А) = ![]() = Т,
= Т,
Следовательно,
1) или Т = 0, то А ≠Е
2) или Т ≠ 0, то c’ (А) = 1 для каждого характера c’? G. В этом случае согласно свойству 3§ 1, имеем А=Е. И тогда Т=h. Таким образом,
Т = ![]() = {
= {![]()
Пусть m – положительное целое число. Определим числовые характеры по модулю m. Мы знаем, что j(m) приведенных классов вычетов по модулю m образуют мультипликативную абелеву группу порядка h=j(m). Мы можем, следовательно, рассмотреть характер этой группы. Но определение характера для приведенных классов вычета по модулю m можно перенести на множество целых чисел следующим образом. Положим
c(а)= c(А), если аÎА,
где А – приведенный класс вычетов по модулю m. Тогда очевидно, c(а)= c(b) (mod m), и c(ab)= c(а) c(b), если (а, m)=(b, m)=1. Поскольку c(А)¹0 для каждого приведенного класса вычетов А, то c(а)¹0, если (a, m)=1.
Это определение применимо только к целым числам а, которые взаимно просты с m.
Мы можем рассмотреть его на все целые числа, положив
c(а)=0, если (a, m)>1.
Следовательно, характер по модулю m есть арифметическая функция c, обладающая следующими свойствами:
c(а)= c(b), если с=b (mod m)
c(ab)= c(a) c(b) для всех целых a и b
c(а)=0, если (a, m)>1
c(а)¹0, если (a, m)=1
Имеется точно j(m) – количество характеров по модулю m, где j(m) – количество положительных целых чисел, не превосходящих m и взаимно простых с m. Они образуют мультипликативную абелеву группу приведенных классов вычета по mod m. Единичным элементом этой группы будет главный характер c1, то есть такой характер, что c1(а)=1, если (а, m)=1. Далее имеем следующее соотношение ортогональности:
![]() = {
= {![]()
![]() = {
= {![]()
Пусть m – положительное целое число. Определим числовые характеры по модулю m. Комплекснозначная функция, определенная для всех целых чисел n, называется числовым характером или характером Дирихле по модулю m, она удовлетворяет следующим условиям:
а) c (n) = 0 тогда и только тогда, когда (n, m) ≠ 1
б) c (n) периодична с периодом m
в) для любых чисел а и b
c (аb) = c (а) c (b)
Функция
c1(n) = {![]()
является числовым характером и называется главным характером. Остальные числовые характеры по модулю m называются неглавными.
Имеет место следующее утверждение о числовых характерах.
Теорема 1 Существует равно φ(m) числовых характеров по модулю m. Если c = c (n) – числовой характер по модулю m, то:
1) для n, взаимно простых с модулем m, значения c (n) есть корень из 1 степени φ(m).
2) для всех n выполняется неравенство /c (n)/ ≤1
3) Имеет место равенство
![]() {
{![]()
4) Для каждого целого числа n
![]() = {
= {![]()
Доказательство. Пусть c (n) – некоторый числовой характер по модулю m. Из пункта б) определения следует, что c (n) задает некоторую функцию c’(![]() ) = c (n) на мультипликативной группе
) = c (n) на мультипликативной группе ![]() классов вычетов по модулю m, взаимно простых с m, а именно
классов вычетов по модулю m, взаимно простых с m, а именно
c’(![]() ) = c (n)
) = c (n)
Здесь ![]() обозначает класс вычетов по модулю m, содержащий n. Так как c(1) ≠ 0, то c’(
обозначает класс вычетов по модулю m, содержащий n. Так как c(1) ≠ 0, то c’(![]() ) не равняется тождественно нулю, а из пункта в) определения числового характера следует, что c’(
) не равняется тождественно нулю, а из пункта в) определения числового характера следует, что c’(![]()
![]() ) = c’(
) = c’(![]() ) = c’ (ab) = c (a) c (b) = c’(
) = c’ (ab) = c (a) c (b) = c’(![]() )c’(
)c’(![]() ).
).
Таким образом, c’(![]() ) есть характер модультипликативной группы Gm.
) есть характер модультипликативной группы Gm.
Обратно, по каждому характеру c’(![]() ) группы Gm можно построить числовой характер c (n) по модулю m, положив
) группы Gm можно построить числовой характер c (n) по модулю m, положив
![]() {
{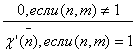
Установленное соответствие является взаимнооднозначным. И все утверждения теоремы 1 следуют из доказанного выше для групповых характеров применительно к группе Gm, если учесть, что порядок группы Gm равен φ(m), где φ(m) – функция Эйлера.
В дальнейшем требуется еще одно утверждение с числовых характерах. Обозначим для каждого c, c ≥ 1
![]()
Где суммирование ведется по всем натуральным числам n, не превосходящим c.
Лемма 2. Пусть c (n) – неглавный характер. Тогда для каждого c, c ≥ 1 справедливо неравенство
/S(x)/<m
Доказательство. Функция c (n) периодична с периодом m и по теореме з
![]() 0, так как c≠ c1
0, так как c≠ c1
Поэтому, представив [c] – целую часть числа c – в виде [c]=m1+z, 0£z£m, будет иметь
S(c) =S([c])=q![]()
![]()
В виду равенства /c(n)/£1 отсюда получили S(c)£z£m
2. L-функция Дирихле
Пусть х(п) – произвольный характер по модулю m. Рассмотрим ряд
![]() , (2.1)
, (2.1)
члены которого являются функциями комплексного переменного S. В области сходимости он определяет функцию, которая называется L-функцией Дирихле, соответствующей характеру c(n), и обозначается L (s, c).
Лемма 3
1. Если c¹c1, то ряд (1) сходится в области ReS > 0 и определяемая им функция L (s, c) является аналитической в этой области.
2. Ряд, определяющий L (S, c1), сходится в области ReS >1. Функция L (S, c1) является аналитической в области ReS > 1.
Доказательство.
Пусть c(n) – произвольный характер по модулю m, а б – некоторое положительное число. Так как /c(n)/ £ 1, то в области ReS > 1 + б справедливо неравенство
![]()
Следовательно, ряд (1) равномерно сходится в области ReS > 1 + б. Определяемая им функция L (S, c) по теореме Вейерштрасса о сумме равномерно сходящегося ряда аналитических функций является аналитической в этой области. Ввиду произвольности 6 это доказывает второе утверждение Леммы.
Для неглавных характеров c(n) потребуется более сложное исследование ряда (1).
Лемма 4 (преобразование Абеля).
Пусть an, n=1,2,…, – последовательность комплексных чисел, c>1,
А(c)=![]()
а q(t) – комплекснозначная функция, непрерывно дифференцируемая на множестве 1£t£¥
Тогда
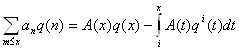 (2.2)
(2.2)
Если же
![]()
то
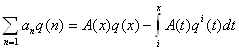 (2.3)
(2.3)
при условии, что ряд в левой части равенства сходится.
Доказательство. Положим А(0)=0 и В(х) равным левой части равенства (2.2). Тогда при любом натуральном N
![]()
так как А(0)=0. Далее

поскольку функция А(х) постоянна на каждом полуинтервале n£t<n+1. Следовательно, равенство (2.2) доказано при целых значениях х.
пусть х³1 – произвольное число. Положим N=[x]; значит, N£x£N+1. Тогда А(х)=А(N), B(x)=B(N), а
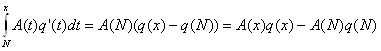
Следовательно,
![]()
Тем самым доказано, что равенство (2.2) верно и для нецелых чисел значений х.
Равенство (2.3) получаем из равенства (2.2) переходом к пределу при х®¥. Лемма доказана.
Воспользовавшись леммой 4, получим следующее равенство
![]() (2.4)
(2.4)
где
![]()
функция, введенная Лемме 4.
Для s = p+it из области ReS = s, где s – некоторое положительное число, пользуясь леммой 4, находим
![]()
Поэтому интеграл

сходится в области ReS > s. Поскольку в этой области выполняется неравенство
![]()
то из равенства (2) следует, что ряд (1), определяющий функцию L (S, x), сходится в области ReS > s. Эти рассуждения справедливы для любого положительного числа s. Значит, ряд (1) сходится в полуплоскости ReS > 0.
Из равенства (2) следует, что в этой полуплоскости для L-функции, соответствующей неглавному характеру c(n), справедливо представление
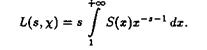
![]() (2.5)
(2.5)
так как
![]()
Интеграл, стоящий в правой части равенства (2.5), можно также представить в виде
 (2.6)
(2.6)
Члены ряда (2.6) являются аналитическими функциями в области ReS >s, что следует из равенств
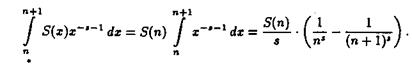
При этом использовано, что на полуинтервале n£х< n+1 функция S(х) принимает значение S(n). Поскольку

то ряд (2.6) равномерно сходится в области ReS >s. Отсюда, как и выше, получаем, что сумма его, т.е.
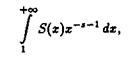
является аналитической функцией (по теореме Вейерштраса) в области ReS >s.
Из представления (2.5) следует теперь, что L (S, x) есть аналитическая функция в полуплоскости ReS >s, а ввиду произвольности S – s и b полуплоскости ReS > 0.
Следствие. Пусть c (n) – произвольный характер. Тогда в области ReS > 1 справедливо равенство
![]() (2.7)
(2.7)
Это следует из того, что ряд (2.1) по доказанному равномерию сходится в области ReS>1+s, где s>0. Следовательно, по теореме Вейштрасса о равномерно сходящихся рядах аналитических функций в этой области ряд (2.1) можно почленно дифференцировать
![]()
Поэтому в полуплоскости ReS>1+s выполняется равенство (2.7). Так как в этом рассуждении s-любое положительное число, то равенство (2.7) будет справедливо в полуплоскости ReS>1.
Для L-функций имеет место представление в виде бесконечного произведения по простым числам, аналогичное тождеству Эйлера. Рассмотрим вспомогательную Лемму.
Лемма 5. Пусть функция f(n) вполне мультипликативна и ряд
![]() (2.8)
(2.8)
абсолютно сходится. Тогда выполняется равенство
![]() (2.9)
(2.9)
Доказательство. Отметим прежде всего, что /f(n)/<1 при любом натуральном n>1. В противном случае при каждом mÎN
/f(n)m/=/f(n)/m³1,
что противоречит сходимости ряда (2.6). Поэтому при каждом простом р ряд
![]()
абсолютно сходится, и его сумма как сумма бесконечно убивающей геометрической прогрессии равна (1-f(р))-1. Кроме этого, в силу абсолютной сходимости, ряды можно перемножить. Перемножая конечное число таких рядов и используя то, что f(n) есть вполне мультипликативная функция, получим
![]()
где ne= pa … pas и в сумме в правой части равенства содержатся такие и только такие слагаемые f(ne), что все просты делители neне превосходят х. Следовательно, в разности
![]()
остаются те и только те слагаемые f(me), для которых у числа me имеется хотя бы один простой делитель р>x. Тогда оценим разность
/S-S(x)/£![]()
и из абсолютной сходимости ряда (2.8) следует, что
![]()
Это доказывает, что бесконечное произведение (2.7) сходится и выполняется утверждение Леммы.
Лемма 6. Для каждого характера c(n) в области ReS > 1 справедливо представление
![]()
Доказательство. Эта лемма является следствием Леммы 5, поскольку функция c(n) вполне мультипликативна, то есть c(АВ)= c(А) c(В), и выполняется неравенство /c(n)/£ 1 по теореме 1.
Следствие 1. В области ReS > 1 для главного характера c1(n) по модулю m справедливо равенство
![]() (2.10)
(2.10)
и поэтому функция L (S, c1) может быть аналитически продолжена в область ReS > 0, где она имеет единственный полюс (первого порядка) в точке S=1.
Действительно, по определению главного характера c1(n) имеет место равенство
![]()
Поэтому
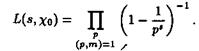
Пользуясь теперь тождеством Эйлера для дзета-функции Римана получаем равенство (2.10). Остальные утверждения легко следуют из этого равенства, поскольку дзета-функция является аналитической в области ReS > 0 с единственным полюсом первого порядка в точке S = 1.
Следствие 2. Для каждого характера c функция L (S, x) не обращается в нуль в области ReS > 1.
Доказательство.
Если s = ReS > 1. то
![]()
Пользуясь неравенством для дзета-функции Римана, находим
![]()
Получаем:
L (S,c) ≥![]()
![]() > 0
> 0
Теперь докажем утверждения, что L – функция, соответствующая неглавному характеру c, точке S =1 отлична от нуля.
Теорема 2. Если c – неглавный характер, то L (1, c)≠0
Для доказательства рассмотрим 2 случая
1. Пусть характер c – комплексное число, не является действительным. Тогда характер c2(n) не является главным. В этом случае доказательство теоремы будет основываться на тех же идеях, что и доказательство отсутствия нулей дзета – функции на прямой ReS=1.
Лемма7. Пусть 0<ч<1, а х – действительное число, тогда выполняется неравенство /(1 – ч)3 (1 – чеix)4 (1 – че2ix)/-1 ≥ 1
Доказательство.
Для всех z из круга /z/<1 имеет место расположение
– ln (1 – z) =![]() (2.11)
(2.11)
Так как ln(t) = Re lnt, то обозначая М (ч φ), левую часть неравенства (2.11), получим
lnM (ч φ) = 3ln (1 – ч) – 4 ln (1 – чеi4) – ln (1 – че2i4) = – 3ln (1-ч) – 4Reln/1 – чеi4/ – Reln/1 – че2i4/=![]() rc (3+4e)inl/1-rei4/=
rc (3+4e)inl/1-rei4/=![]() (3+4cosnl+2cos2nl)=
(3+4cosnl+2cos2nl)= ![]() (2+4cosa+1+cos2a)=
(2+4cosa+1+cos2a)=![]() 1 (1+cosa)2³0
1 (1+cosa)2³0
ln=M (r, l)=³0
Следовательно, M (r, l)=³1 доказана.
Из леммы 7 следует, сто при любом действительном S>1 выполняется равенство:
|L3(8, c1) L4(S, c) 4 (S, c4) 1 = П (1- ![]() )3(1-
)3(1- ![]() )4(1-
)4(1- ![]() )|-1 (2.12)
)|-1 (2.12)
Получая в лемме ч = р-s, т.е.
0< ч = c1(р)<1
0< р-s<1
c (р) р-s = чеi4, в силу того что c (р) – комплексное
c (р) р-s= че2i4
Получаем, что каждый сомножитель в правой части равенства (f) не меньше 1 и, следовательно, при любом S>1 выполняется равенство:
|L3(Sc1) · L4(Sc) L (Sc2)| ≥ 1 (2.13)
Допустим, что для некоторого характера c (c2≠c1) выполняется равенство
L (1, c) = 0 (2.14)
Оценим сверху левую часть неравенства. Из оценки дзета-функции Римана
ξ(S) ≤ ![]() , следует, что при S ? R, S>1 выполняется неравенство
, следует, что при S ? R, S>1 выполняется неравенство
а) 0 < 4 (S, c1) = 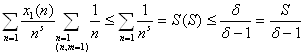
получили 0<L (S, c1)≤![]()
б) Функция L (S, c) разложим в ряд Тейлора
L (S, c) = Cp + C1 (S – 1) + C2(S – 1)2 +… + Cn(S – 1)n +…
Предположим, что у нее есть нуль L (1, c) = 1; тогда С0 = 0
Перепишем разложение L – функции в ряд
L(Sc) = Cк (S – 1)к + Ск+1(S – 1)к+1 = (S – 1)1 (Cк + Ск+1(S -1)+….), где к≥1, Ск ≤ 0, т. к. S>1
| L (S, c)| = |S – 1|k| Ck + Ck+1(S – 1) +….| ≤ 2 Ck|S – 1)k, при |S – | < r
Функция L (S, c2) в точке S = 1 не имеет полюса, следовательно не имеет особенности. Это в силу того, что c комплексное и c2≠c1
Получаем неравенство:
L (S, c2) ≤ C,
При условии | S – 1|< δ
Учитывая все неравенства и оценки
| L3 (S, c) L4(S, c) L (S, c2)| = (![]() )3 · 24 |Ck|4 (S – 1)4k· C≥1
)3 · 24 |Ck|4 (S – 1)4k· C≥1
Следовательно, это неравенство становится противоречивым, если перейти к пределу при S→1+0. Полученное противоречие показывает, что равенство (2.14) не выполняется.
Похожие работы
... . Упражнение. Доказать, что, если на всей оси функция y(х) дифференцируема, а j(х) – дважды дифференцируема, то функция (13.11) действительно удовлетворяет уравнению (13.9) и начальным условиям (13.10). Глава 3. Операционное исчисление § 14. Преобразование Лапласа Понятие оригинала. Кусочно-непрерывная функция называется оригиналом, если выполняются следующие условия: 1) для всех ...
... на ak может быть не более чем ak - 1 (ведь ни одно число не даёт остаток rk), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа M + sd и M + td (0 Ј s Ј ak - 1 и 0 Ј t Ј ak - 1). Тогда их разность (M + sd) - (M + td) = (s - t)d делится на ak, что невозможно, т.к. 0 < |s - t| < ak и d = a1a2...ak - 1 взаимно просто с ak, ибо числа a1, a2, . . ., ak ...
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
... рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение =, , , , , … 0,3; 0,42; 0,45; 0,467; … Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида. Например, имеется разложение =, , , , , , , … 1; 1,5; 1,38; 1,44; 1,40; … Но самое интересное и важное это то, что в то время как до настоящего ...
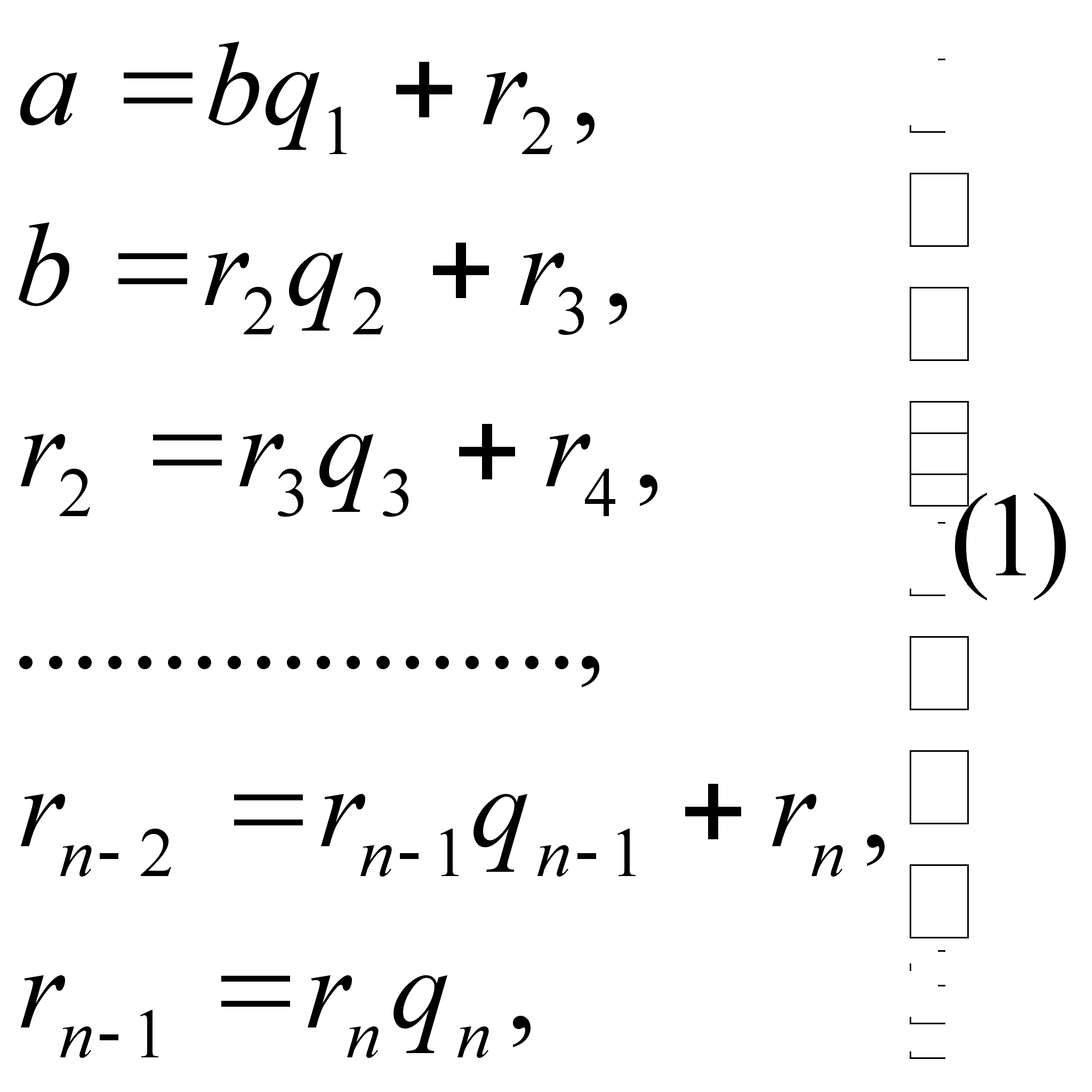
0 комментариев