Навигация
2. Расчетная часть
Исходные данные
Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности в отчетном году (выборка 20 %-ная механическая), млн. руб.:
| № № предприятия п/п | Фонд заработной платы млн. руб. | Среднесписочная численность работников чел | № предприятия п/п | Фонд заработной платы млн. руб. | Среднесписочная численность работников чел |
| 1 | 11,340 | 162 | 16 | 11,502 | 162 |
| 2 | 8,112 | 156 | 17 | 16,356 | 188 |
| 3 | 15,036 | 179 | 18 | 12,792 | 164 |
| 4 | 19,012 | 194 | 19 | 17,472 | 192 |
| 5 | 13,035 | 165 | 20 | 5,85 | 130 |
| 6 | 8,532 | 158 | 21 | 9,858 | 159 |
| 7 | 26,400 | 220 | 22 | 11,826 | 162 |
| 8 | 17,100 | 190 | 23 | 18,142 | 193 |
| 9 | 12,062 | 163 | 24 | 8,848 | 158 |
| 10 | 9,540 | 159 | 25 | 13,944 | 168 |
| 11 | 13,694 | 167 | 26 | 23,920 | 208 |
| 12 | 21,320 | 205 | 27 | 13,280 | 166 |
| 13 | 16,082 | 187 | 28 | 22,356 | 207 |
| 14 | 10,465 | 161 | 29 | 10,948 | 161 |
| 15 | 4,32 | 120 | 30 | 15,810 | 186 |
Задание 1
Признак – Среднегодовая заработная плата (определите как отношение фонда заработной платы к среднесписочной численности работников).
Число групп – пять.
Решение:
Прежде всего, рассчитаем среднегодовую заработную плату работников на каждом предприятии, как указано в задании, и отсортируем их по возрастанию заработной платы для удобства дальнейших расчётов; результаты отразим в таблице 2.1.
Таблица 2.1
Таблица результатов расчета среднегодовой заработной платы (предприятия отсортированы по возрастанию заработной платы)
| № п/п | Фонд заработной платы, млн. руб. | Среднесписочная численность работников, чел. | Среднегодовая заработная плата, тыс. руб./чел. |
| 15 | 4,32 | 120 | 36 |
| 20 | 5,85 | 130 | 45 |
| 2 | 8,112 | 156 | 52 |
| 6 | 8,532 | 158 | 54 |
| 24 | 8,848 | 158 | 56 |
| 10 | 9,54 | 159 | 60 |
| 21 | 9,858 | 159 | 62 |
| 14 | 10,465 | 161 | 65 |
| 29 | 10,948 | 161 | 68 |
| 1 | 11,34 | 162 | 70 |
| 16 | 11,502 | 162 | 71 |
| 22 | 11,826 | 162 | 73 |
| 9 | 12,062 | 163 | 74 |
| 18 | 12,792 | 164 | 78 |
| 5 | 13,035 | 165 | 79 |
| 27 | 13,28 | 166 | 80 |
| 11 | 13,694 | 167 | 82 |
| 25 | 13,944 | 168 | 83 |
| 3 | 15,036 | 179 | 84 |
| 30 | 15,81 | 186 | 85 |
| 13 | 16,082 | 187 | 86 |
| 17 | 16,356 | 188 | 87 |
| 8 | 17,1 | 190 | 90 |
| 19 | 17,472 | 192 | 91 |
| 23 | 18,142 | 193 | 94 |
| 4 | 19,012 | 194 | 98 |
| 12 | 21,32 | 205 | 104 |
| 28 | 22,356 | 207 | 108 |
| 7 | 26,4 | 220 | 120 |
| 26 | 23,92 | 208 | 115 |
| 7 | 26,4 | 220 | 120 |
Для того чтобы разбить данные предприятия на пять групп с равными интервалами по среднегодовой заработной плате, необходимо рассчитать величину шага разбиения по формуле:
i = (Xmax-Xmin)/n, где n – число образуемых групп.
i = (120 - 36) / 5 = 16,8 (тыс. руб./чел.).
Распределение предприятий по группам по среднегодовой заработной плате продукции представлено в таблице 2.2.
Таблица 2.2
Распределение предприятий по уровню рентабельности
| Группы предприятий по среднегодовой заработной плате | Интервал, тыс. руб./чел. | Количество предприятий | Кумулятивная частота | |
| 1 | 36,0 | 52,8 | 3 | 3 |
| 2 | 52,8 | 69,6 | 6 | 9 |
| 3 | 69,6 | 86,4 | 12 | 21 |
| 4 | 86,4 | 103,2 | 5 | 26 |
| 5 | 103,2 | 120,0 | 4 | 30 |
| Итого: | 30 | - | ||
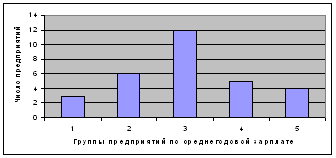 |
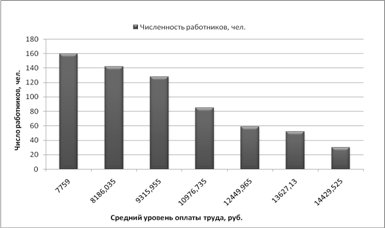
Согласно данным таблицы 2.2 построим графики полученного ряда распределения.
Рис. 2.1: Гистограмма распределения предприятий по уровню заработной платы
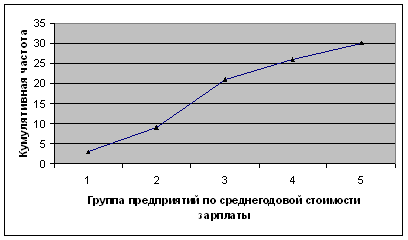 |
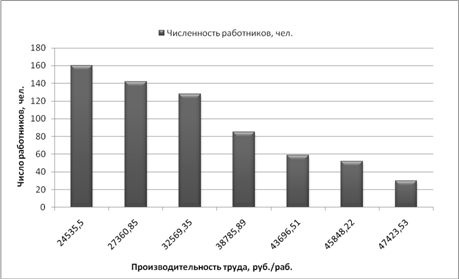
Рис. 2.2: Кумулята распределения предприятий по уровню рентабельности
По графикам видно, что Мо = 78, а Ме = 69,6. Конечно, при определении значений по графикам имеет место небольшая погрешность.
Для расчёта средней арифметической, среднего квадратического отклонения, коэффициента вариации применяем формулы во взвешенной форме, так как данные сгруппированы и представлены в виде интервального ряда.
Для расчета указанных величин нам понадобятся некоторые промежуточные данные, представленные в таблице 2.3
Таблица 2.3
Данные для расчёта средней арифметической, среднего квадратического отклонения, коэффициента вариации
| № группы | Интервал | Число п/п (fi) | Середина интервала (хi) | хi* fi | хi2* fi | хi-ха | (хi-ха)2* fi | |
| 1 | 36,0 | 52,8 | 3 | 44,4 | 133,2 | 5914,08 | -34,16 | 3500,72 |
| 2 | 52,8 | 69,6 | 6 | 61,2 | 367,2 | 22472,64 | -17,36 | 1808,22 |
| 3 | 69,6 | 86,4 | 12 | 78,0 | 936 | 73008 | -0,56 | 3,76 |
| 4 | 86,4 | 103,2 | 5 | 94,8 | 474 | 44935,2 | 16,24 | 1318,69 |
| 5 | 103,2 | 120,0 | 4 | 111,6 | 446,4 | 49818,24 | 33,04 | 4366,57 |
| Итого | 30 | - | 30 | - | 2356,8 | 196148,16 | - | 10997,95 |
1) Для расчёта средней арифметической используется следующая формула:
ха = ∑ хifi / ∑ fi = 2356,8/30 = 78,56 тыс. руб./чел.
2) Расчёт средней квадратической произведём по формуле:
![]()
![]() хкв = ∑ хi2fi / ∑ fi = 196148,16/30 = 80,86
хкв = ∑ хi2fi / ∑ fi = 196148,16/30 = 80,86
3) Среднее квадратическое отклонение высчитывается по формуле:
σ = ∑(хi-ха)2 fi / ∑ fi = 10997,95/30 = 19,147 тыс. руб./чел.
4) Тогда коэффициент вариации будет равен:
Vδ = σ /ха = (19,147/78,56)100 = 24,4%
Теперь вычислим среднюю арифметическую по данным таблицы 5, расчёт будем производить по формуле:
ха = ∑ хi / n = 2350/30 = 78,33 тыс. руб./чел.
Полученный результат отличен от приведённого выше, так как в данном случае расчет проводился для несгруппированных данных, представленных в виде дискретного ряда. Следовательно, расчёт проводился по формуле средней арифметической простой.
Таким образом, по результатам задания №1 можно сделать такой вывод: коэффициент вариации (24,4%) не превышает 33%, что говорит о том, что найденная средняя заработная плата является типичной характеристикой, а также об однородности совокупности предприятий по данному признаку.
Задание 2
Связь между признаками – фонд заработной платы и среднегодовая заработная плата
Решение:
Сначала установим связь между указанными признаками методом аналитической группировки. В качестве факторного признака будет выступать фонд заработной платы работников предприятия, а в качестве результативного – среднегодовая заработная плата. Сначала необходимо рассчитать величину интервала: i = (26,4 – 4,3)/5 = 4,42
Результаты группировки отражены в таблицах 2.4 и 2.5 (для составления таблицы 2.5 будут использоваться данные из таблицы 2.4).
Таблица 2.4
Зависимость рентабельности от объёма выпуска продукции
| Группы предприятий по размеру фонда оплаты труда | Интервал | Количество предприятий | Среднегодовая заработная плата, тыс.руб./чел. | ||
| всего | в среднем на 1 предприятие | ||||
| 1 | 4,3 | 8,72 | 4 | 187 | 46,75 |
| 2 | 8,72 | 13,14 | 11 | 756 | 68,73 |
| 3 | 13,14 | 17,56 | 9 | 768 | 85,33 |
| 4 | 17,56 | 21,98 | 3 | 296 | 98,67 |
| 5 | 21,98 | 26,4 | 3 | 343 | 114,33 |
| Итого: | 30 | 2350 | 78,33 | ||
Таблица 2.5
Корреляционная таблица
| Группы предприятий по размеру ФОТ | 4,3 – 8,72 | 8,72 –13,14 | 13,14-17,56 | 17,56-21,98 | 21,98 – 26,4 | Частота | |
| Группы предприятий по уровню зарплаты | |||||||
| 36,0 | 52,8 | 3 | - | - | - | - | 3 |
| 52,8 | 69,6 | 1 | 5 | - | - | - | 6 |
| 69,6 | 86,4 | - | 6 | 6 | - | - | 12 |
| 86,4 | 103,2 | - | - | 3 | 2 | - | 5 |
| 103,2 | 120,0 | - | - | - | 1 | 3 | 4 |
| Частота | 4 | 11 | 9 | 3 | 3 | 30 | |
Теперь измерим тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения. Для удобства расчёта указанных показателей представим в таблице 2.6 некоторые промежуточные данные.
Таблица 2.6
Промежуточные расчеты
| Показатель | x1 | х2 | х3 | х4 | х5 | ха | x1-xa | х2-xa | х3-xa | х4-xa | х5-xa |
| Значение | 46,75 | 68,73 | 85,33 | 98,67 | 114,33 | 78,33 | -31,58 | -9,6 | 7,0 | 20,34 | 36 |
х1 – х5 – групповые средние (хj); ха – общая средняя.
Общую дисперсию рассчитаем по формуле:
Σобщ2 = (∑ хi2 / n)-( ∑ хi / n)2;
Σобщ2 = (195626/30)-(78,33)2 = 385,28
Величина межгрупповой дисперсии определяется по следующей формуле:
Δ2 = ∑(хj-ха)2 nj / ∑nj , где nj – число единиц в j-той группе
После вычисления имеем: δ2 = 352,44.
Теперь мы имеем все данные для расчёта коэффициента детерминации (η2)и эмпирического корреляционного отношения (η).
![]()
η2 = δ2/σобщ2 η = δ2/σобщ2
![]() η2 = (352,44/385,28)*100 = 91,5%;
η2 = (352,44/385,28)*100 = 91,5%;
η = 352,44/385,28 = 0,956
Таким образом, по результатам выполнения задачи №2 можно сделать следующие выводы:
из таблицы 2.4 видно, что с ростом фонда оплаты труда от группы к группе, увеличивается и среднегодовая заработная плата от группы к группе. Следовательно, связь между рассматриваемыми признаками прямая корреляционная;
выводы, сделанные в п.1) подтверждаются и корреляционной таблицей, где присутствует ярко выраженное распределение предприятий вдоль диагонали (таблица 2.5);
коэффициента детерминации (91,5%) показывает, что среднегодовая зарплата почти на 91,5% объясняется различием в размере фонда оплаты труда и только на 8,5% - другими признаками;
эмпирическое корреляционное отношение (0,956, т.е. близко к единице) свидетельствует, что на среднегодовую зарплату существенно влияет размер фонда оплаты труда.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
Ошибку выборки среднегодовой заработной платы и границы, в которых будет находиться уровень среднегодовой заработной платы в генеральной совокупности.
Ошибку выборки доли организаций с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более и границы, в которых будет находится генеральная доля.
Решение:
![]() Расчёт ошибки выборки среднего уровня рентабельности будем производить по формуле:
Расчёт ошибки выборки среднего уровня рентабельности будем производить по формуле:
Δх = tμх = (σ2/n)(1-n/N)
![]() а ошибку выборки доли организаций с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более по следующей формуле:
а ошибку выборки доли организаций с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более по следующей формуле:
Δw = tμw = (w(1-w)/n)(1-n/N)
Данные, необходимые для расчёта, представлены в следующей таблице
Таблица 2.7
| Показатель | P | t | N, шт. | n, шт. | xa, тыс.руб./чел. | σ | w |
| Значение | 0,954 | 2,0 | 150 | 30 | 78,33 | 19,147 | 0,300 |
Р – доверительная вероятность;
t – коэффициент доверия;
n – число единиц выборочной совокупности;
N – число единиц генеральной совокупности;
w – доля единиц, обладающих данным признаком;
σ – среднее квадратическое отклонение.
![]()
Δх = 2,0 ((19,147)2/30)(1-30/150) = 6,25 (тыс. руб./чел.)
Таким образом, среднегодовая заработная плата на предприятиях генеральной совокупности с вероятностью 0,954 будет находиться в промежутке: 72,08 ≤ 78,33 ≤ 84,58.
![]()
Δw = 2,0 (0,30(1- 0,30)/30)(1-30/150) = 0,149
Следовательно, от 15,1 до 44,9% организаций с вероятностью 0,954 будут превышать уровень среднегодовой зарплаты 86,4 тыс. руб./чел.
Задание 4
Имеются следующие данные по двум организациям:
| Организация | базисный период | отчетный период | ||
| Средняя заработная плата, руб. | Среднесписочная численность работников, чел. | Средняя заработная плата, руб. | Фонд заработной платы, тыс. руб | |
| 1 | 5000 | 100 | 6500 | 682,5 |
| 2 | 5600 | 100 | 8000 | 760,0 |
Определите:
Похожие работы
... труде наемного работника. Автор "Капитала" излагает свое представление о заработной плате, переходя от простого к сложному: от анализа сущности стоимости и цены рабочей силы к характеристике превращения стоимости и цены рабочей силы в заработную плату и особенностей ее форм - повременной и сдельной (поштучной). Так или иначе, на заработную плату влияют как продолжительность рабочего времени, ...
... пенсионные фонды, зачисляемые на личные счета работников, включаются наряду с другими материальными и социальными благами в денежном выражении в состав совокупного налогооблагаемого дохода работника. 1.5. Методика анализа фонда заработной платы Анализ фонда оплаты труда проводят по тому же плану, что и анализ других видов расходов: по сравнению с нормативной или плановой величиной либо ...
... план по договорным обязательствам, по объему перевозок, по номенклатуре грузов. Чем ближе значение показателя к 100%, тем ритмичнее работа автотранспортного предприятия, коэффициент ритмичности на рассматриваемом предприятии 100,46. 3. Статистическое изучение основного капитала По данным бухгалтерского учета стоимость основного капитала и его элементов известна по состоянию на начало и ...
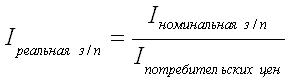
... так и реальной заработной плате Глава 2. Статистический анализ данных финансовой отчетности по оплате труда на ОАО «Бумажная Фабрика «Коммунар» В курсовой работе статистический анализ оплаты труда изучается на примере ОАО «Бумажная Фабрика «Коммунар». ОАО «Бумажная Фабрика «Коммунар» известный в России и за рубежом производитель упаковочных и технических видов бумаг и картона плотностью ...

0 комментариев