Навигация
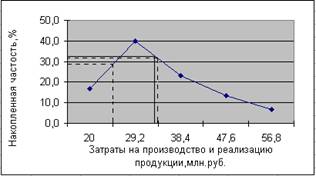
Рассчитаем основные характеристики ряда распределения
3. Рассчитаем основные характеристики ряда распределения.
Для расчёта основных характеристик построим рабочую таблицу 6. Перейдём от интервального ряда к дискретному, заменив интервальные значения их средними значениями (простая средняя между нижней и верхней границами интервала).
Таблица 6 Таблица расчёта основных характеристик
| Группы предприятий по выпуску продукции, млн. руб. | Число предприятий | Середина интервала |
|
|
| |
| 14,4 | 27,36 | 4 | 20,88 | 83,52 | 435,97 | 1743,88 |
| 27,36 | 40,32 | 8 | 33,84 | 270,72 | 1145,15 | 9161,2 |
| 40,32 | 53,28 | 9 | 46,8 | 421,2 | 2190,24 | 19712,16 |
| 53,28 | 66,24 | 6 | 59,76 | 358,56 | 3571,26 | 21427,56 |
| 66,24 | 79,2 | 3 | 72,72 | 218,16 | 5288,20 | 15,864,6 |
| 30 | 1352,16 | 52044,8 | ||||
Найдём среднюю арифметическую:
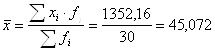 млн. руб.
млн. руб.
– уровень выпуска продукции на каждом предприятии за отчётный год составил в среднем 45,072 млн. руб.
Дисперсия признака – это средний квадрат отклонений вариантов от их средней величины:
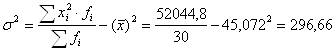
Среднее квадратическое отклонение показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения и численно равно корню квадратному из дисперсии:
![]() (млн. руб.)
(млн. руб.)
Коэффициент вариации:
![]()
Значение коэффициента меньше 40%, следовательно, вариация производительности в данной совокупности незначительна, а совокупность однородна.
3. Рассчитаем среднее значение выпуска продукции по исходным данным по формуле средней арифметической простой:
![]() (млн. руб.)
(млн. руб.)
Полученное значение отличается от значения в п. 3 т. к. в п. 3 вычисления происходили по сгруппированным данным, причём, для расчётов брались приближённые значения вариант (середины интервалов).
Задание 2
По исходным данным табл. 1:
1. Установите наличие и характер связи между признаками среднесписочная численность работников и выпуск продукции, образовав пять групп с равными интервалами по обоим признакам, методами:
а) аналитической группировки,
б) корреляционной таблицы.
2. Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициента детерминации и эмпирического корреляционного отношения.
Сделайте выводы.
Решение:
Построим аналитическую группировку предприятий по уровню среднесписочной численности работников. Факторным признаком в данном случае будет являться среднесписочная численность работников, а результативным – уровень выпуска продукции.
Ранжируем исходные данные в порядке возрастания численности рабочих. Результаты расчётов для построения аналитической группировки представим в таблице 7.
Таблица 7. Ранжированный ряд по признаку численность работников
| № | Численность работников, чел. | Итого | Выпуск продукции, млн. руб.
| Итого |
| Дисперсия |
| 15 | 120 | 14,4 | 207,36 | |||
| 20 | 130 | 250 | 18,2 | 32,6 | 331,24 | 3,61 |
| 2 | 156 | 23,4 | 547,56 | |||
| 6 | 158 | 26,86 | 721,46 | |||
| 24 | 158 | 28,44 | 808,83 | |||
| 10 | 159 | 30,21 | 912,64 | |||
| 21 | 159 | 790 | 31,8 | 140,69 | 1011,24 | 8,599 |
| 14 | 161 | 35,42 | 1254,57 | |||
| 29 | 161 | 35,903 | 1289,03 | |||
| 1 | 162 | 36,45 | 1328,6 | |||
| 16 | 162 | 36,936 | 1364,27 | |||
| 22 | 162 | 39,204 | 1536,95 | |||
| 9 | 163 | 40,424 | 1634,1 | |||
| 18 | 164 | 41 | 1681 | |||
| 5 | 165 | 41,415 | 1715,2 | |||
| 27 | 166 | 41,832 | 1749,92 | |||
| 11 | 167 | 42,418 | 1799,29 | |||
| 25 | 168 | 43,344 | 1878,7 | |||
| 3 | 179 | 1980 | 46,54 | 480,886 | 2165,97 | 10,541 |
| 30 | 186 | 50,22 | 2522,05 | |||
| 13 | 187 | 51,612 | 2663,8 | |||
| 17 | 188 | 53,392 | 2850,71 | |||
| 8 | 190 | 54,72 | 2994,28 | |||
| 19 | 192 | 55,68 | 3100,26 | |||
| 23 | 193 | 57,128 | 3263,6 | |||
| 4 | 194 | 1330 | 59,752 | 382,504 | 3570,3 | 9,143 |
| 12 | 205 | 64,575 | 4169,93 | |||
| 28 | 207 | 69,345 | 4808,73 | |||
| 26 | 208 | 70,82 | 5015,47 | |||
| 7 | 220 | 840 | 79,2 | 283,94 | 6272,64 | 27,822 |
| 4940 | 1288,02 | 65169,7 | 56,105 |
Величина интервала:
![]() чел.
чел.
Xmax и Х min - соответственно максимальная и минимальная численность рабочих.
Получаем следующие интервалы численности рабочих, чел.:
Таблица 8. Интервалы численности рабочих
| Нижняя граница | Верхняя граница |
| 120 | 140 |
| 140 | 160 |
| 160 | 180 |
| 180 | 200 |
| 200 | 220 |
Результаты группировки представим в таблице 9.
Таблица 9. Группировка предприятий по численности рабочих:
| Группы предприятий по численности рабочих, чел. | Число предприятий | Выпуск продукции, млн. руб. | ||
| Всего | В среднем на 1 предприятие | |||
| 120 | 140 | 2 | 32,6 | 16,3 |
| 140 | 160 | 5 | 140,69 | 28,138 |
| 160 | 180 | 12 | 480,886 | 40,074 |
| 180 | 200 | 7 | 382,504 | 54,643 |
| 200 | 220 | 4 | 283,94 | 70,985 |
| Итого | 30 | 1288,02 | 42,934 | |
Из таблицы видно, что между численностью рабочих и уровнем выпуска продукции существует прямая корреляционная связь. С ростом численности рабочих от группы к группе растёт средний уровень выпуска продукции на каждое предприятие.
Для оценки тесноты этой связи рассчитаем коэффициент детерминации и эмпирическое корреляционное отношение.
Общая дисперсия характеризует вариацию результативного признака, которая зависит от всех условий, влияющих на совокупность. В данном случае она характеризует вариацию выпуска продукции под воздействием всех факторов в данной совокупности.
![]()
Рассчитаем среднюю из внутригрупповых дисперсий. В данном случае эта дисперсия характеризует вариацию выпуска продукции за счёт факторов, не положенных в основу группировку:
![]()
![]()
Рассчитаем межгрупповую дисперсию. Межгрупповая дисперсия характеризует вариацию результативного признака, вызываемую фактором, положенным в основание группировки. В данном случае она характеризует вариацию выпуска под влиянием изменения численности рабочих:
![]()
Коэффициент детерминации определяется по формуле:
![]()
Расчёты показали, что вариация объёма продукции на 96,43% обусловлена вариацией численности рабочих.
Эмпирическое корреляционное отношение рассчитывается как корень квадратный из коэффициента детерминации и характеризует тесноту связи между результативным и факторным признаками:
![]()
Таким образом, между объёмом продукции и численностью рабочих существует достаточно тесная прямая корреляционная связь.
Проверим значимость коэффициента детерминации с помощью F-критерия Фишера:
![]()
При уровне значимости ![]() , числе степеней свободы
, числе степеней свободы ![]() и
и ![]() табличная величина F = 2,69, поэтому значение коэффициента детерминации признаётся существенным.
табличная величина F = 2,69, поэтому значение коэффициента детерминации признаётся существенным.
Построим корреляционную таблицу (табл. 10).
Таблица 10. Корреляционная таблица
| Группы предприятий по производительности, тыс. руб. | Группы предприятий по численности рабочих, чел. | Итого | ||||
| 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | ||
| 14,4-27,36 | 2 | 2 | 4 | |||
| 27,36-40,32 | 3 | 5 | 8 | |||
| 40,32-53,28 | 7 | 2 | 9 | |||
| 53,28-66,24 | 5 | 1 | 6 | |||
| 66,24-79,2 | 3 | 3 | ||||
| Итого | 2 | 5 | 12 | 7 | 4 | 30 |
Как видно из данных таблицы 9, распределение числа предприятий произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол, т.е., увеличение численности рабочих сопровождалось ростом объёмов выпуска продукции.
Характер распределения частот по диагонали корреляционной таблицы свидетельствует о наличии прямой корреляционной связи между изучаемыми признаками.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки среднего уровня выпуска продукции и границы, в которых будет находиться выпуск в генеральной совокупности.
2. Ошибку выборки доли организаций с выпуском продукции 53,28 млн. руб. и более и границы, в которых будет находиться генеральная доля.
Решение:
1. Найдём среднюю ошибку выборки, которая показывает, какие отклонения возможны между характеристиками генеральной и выборочной совокупностей, по формуле собственно – случайной бесповторной выборки:
Дано:
Доверительная вероятность 0,954; t=2 (коэффициент кратности при доверительной вероятности 0,954).
![]() - процент выборки
- процент выборки
Величина возможной случайной ошибки репрезентативности характеризуется средней ошибкой выборки. Она показывает, какие возможны отклонения между характеристиками генеральной и выборочной совокупностей, и при бесповторном отборе, как в данном случае, находится по формуле:
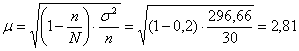 млн. руб.
млн. руб.
Найдем предельное отклонение. Оно равно произведению коэффициента кратности t средней ошибки (показывает, сколько средних ошибок находится в предельной ошибке с заданной вероятностью) на величину средней ошибки. В данном случае:
![]() млн. руб.
млн. руб.
Найдем предельную ошибку выборки, то есть, в каких пределах находится средняя сумма прибыли отрасли в генеральной совокупности:
![]()
![]()
![]()
С вероятностью 0,954 можно утверждать, что средний выпуск продукции в генеральной совокупности будет находиться в пределах от 39,452 до 50,692 млн. руб.
2. Выборочная доля определяется отношением числа единиц, обладающих изучаемым признаком, к общему числу единиц выборочной совокупности:
n – общее число предприятий выборочной совокупности (30):
m – число предприятий с выпуском 53,28 млн. руб. и более.
![]()
Найдём среднюю ошибку выборки для доли, которая показывает, какие возможны отклонения между характеристиками генеральной и выборочной совокупностей, по формуле собственно-случайной бесповторной выборки:
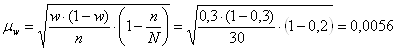
![]() млн. руб.
млн. руб.
предельное отклонение для заданной доверительной вероятности равно средней ошибке.
Найдем в каких пределах находится генеральная доля:
Р- генеральная доля совокупности;
![]()
![]()
![]()
![]()
Значит с вероятностью 0,954 можно утверждать, что генеральная доля предприятий с выпуском продукции 53,28 млн. руб. и более будет находиться в пределах от 0,2888 до 0,3112 (от 28,88% до 31,12%).
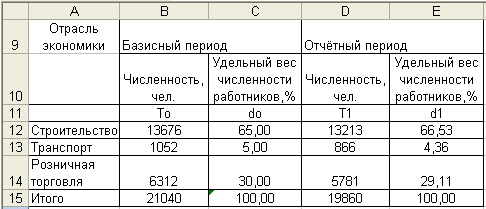
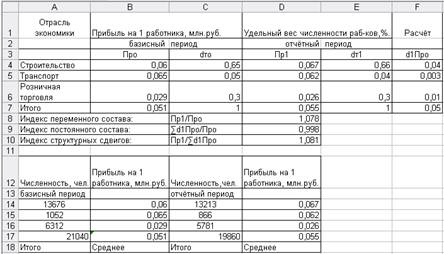
Задание 4
Имеются следующие данные о производстве продукции и среднесписочной численности работников организации:
Таблица 11 Исходные данные
| Филиалы организации | Базисный период | Отчётный период | ||
| Выпуск продукции, млн. руб. | Численность работников, чел. | Выпуск продукции, млн. руб. | Численность работников, чел. | |
| №1 | 50 | 180 | 80 | 200 |
| №2 | 70 | 200 | 90 | 200 |
Определите:
1.По каждому филиалу уровни и динамику производительности труда.
Результаты расчетов представьте в таблице.
2.По организации в целом:
- индексы производительности труда (переменного, постоянного состава, структурных сдвигов);
- абсолютное изменение средней производительности труда за счет отдельных факторов.
- абсолютное изменение выпуска продукции вследствие изменения среднесписочной численности работников, производительности труда и двух факторов вместе.
Решение:
Похожие работы
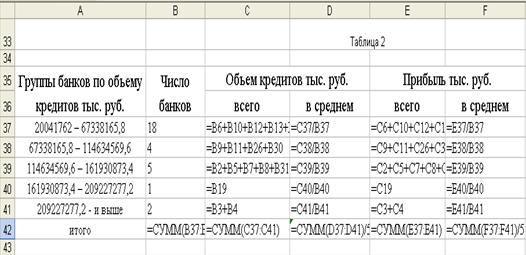
... , которые применяются для выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях. 3. Показатели деятельности коммерческих банков При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающими. Такие интервалы ...
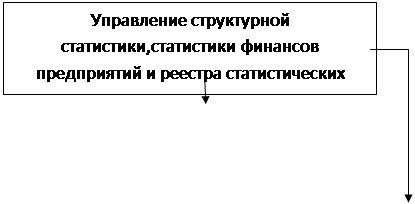
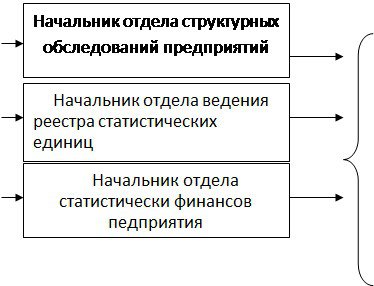
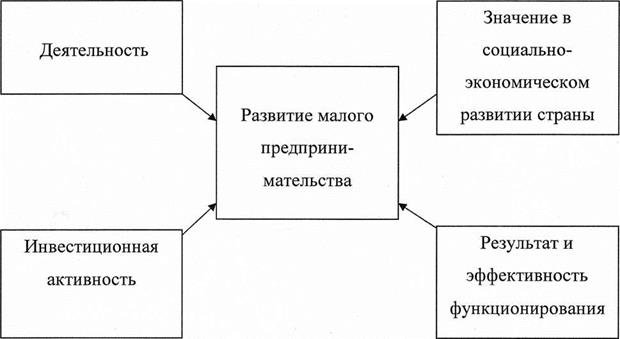
... и зарубежных ученных- экономистов; дано определение предпринимательство в составе с хозяйственным Кодексом Украины. РАЗДЕЛ 2. ИНФОРМАЦИОННО АНАЛИТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ СТАТИСТИЧЕСКОГО ИЗУЧЕНИЕ ПРЕДПРИНИМАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ 2.1 Характеристика деятельности управления структурной статистики, статистики финансов и реестра статистических единиц Управление структурной статистики, статистики финансов ...
... рассчитывается по формуле Норма доходности = Доход по ссуде – Расходы по ссуде / Величина ссуды. 2. Методы анализа результатов деятельности коммерческих банков 2.1 Индексный метод Для анализа кредитных вложений и их динамики широко используют такой статистический метод, как индексный. Индексный метод позволяет проанализировать факторы изменения скорости оборачиваемости операций. В этом ...
... из одной единицы, обладающей всем объёмом признака. Минимальное значение приближается к нулю, но его никогда ни достигает. [2; 135] 2. Расчётная часть 2.1. Условие задач Для анализа финансовых результатов деятельности предприятий одной из отраслей экономики произведена 10% -ная механическая выборка, в результате которой получены следующие данные млн. руб.: № предприятия п/п ...
0 комментариев