Навигация
Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. P > [2/3(n-2) – 1, 96 √ (16n-29)/90]
3.2. Проверку случайности уровней ряда остатков проведем на основе критерия поворотных точек. P > [2/3(n-2) – 1, 96 √ (16n-29)/90]
Количество поворотных точек равно 6 (рис.4.5).
Рис. 4.5

Неравенство выполняется (6 > 2). Следовательно, свойство случайности выполняется. Модель по этому критерию адекватна.
3.3. Соответствие ряда остатков нормальному закону распределения определим при помощи RS – критерия:
![]() , где
, где
![]() - максимальный уровень ряда остатков,
- максимальный уровень ряда остатков, ![]()
![]() - минимальный уровень ряда остатков,
- минимальный уровень ряда остатков, ![]()
![]() - среднеквадратическое отклонение,
- среднеквадратическое отклонение,
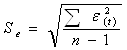 ,
, ![]()
![]()
Расчетное значение попадает в интервал (2,7-3,7), следовательно, выполняется свойство нормальности распределения. Модель по этому критерию адекватна.
3.4. Проверка равенства нулю математического ожидания уровней ряда остатков.
В нашем случае ![]() , поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
В таблице 4.3 собраны данные анализа ряда остатков.
Таблица 4.3
| Проверяемое свойство | Используемые статистики | Граница | Вывод | ||
| наименование | значение | нижняя | верхняя | ||
| Независимость | d-критерий | 0,85 | 1,08 | 1,36 | неадекватна |
| Случайность | Критерий поворотных точек | 6>2 | 2 | адекватна | |
| Нормальность | RS-критерий | 2,81 | 2,7 | 3,7 | адекватна |
| Среднее=0? | t-статистика Стьюдента | 0 | -2,179 | 2,179 | адекватна |
| Вывод: модель статистики неадекватна | |||||
4) Оценить точность модели на основе использования средней относительной ошибки аппроксимации.
Для оценки точности полученной модели будем использовать показатель относительной ошибки аппроксимации, который вычисляется по формуле:
![]() , где
, где ![]()
Расчет относительной ошибки аппроксимации
Таблица 4.4
| t | Y | Предсказанное Y |
|
| |
| 1 | 5 | 4,58 | 0,42 | 0,08 | |
| 2 | 7 | 7,21 | -0,21 | 0,03 | |
| 3 | 10 | 9,84 | 0,16 | 0,02 | |
| 4 | 12 | 12,48 | -0,48 | 0,04 | |
| 5 | 15 | 15,11 | -0,11 | 0,01 | |
| 6 | 18 | 17,74 | 0,26 | 0,01 | |
| 7 | 20 | 20,38 | -0,38 | 0,02 | |
| 8 | 23 | 23,01 | -0,01 | 0,00 | |
| 9 | 26 | 25,64 | 0,36 | 0,01 | |
| Сумма | 45 | 136 | 0,00 | 0,23 | |
| Среднее | 5 | 15,11 |
![]()
Если ошибка, вычисленная по формуле, не превосходит 15%, точность модели считается приемлемой.
5) По построенной модели осуществить прогноз спроса на следующие две недели (доверительный интервал прогноза рассчитать при доверительной вероятности р = 70%).
![]()
![]()
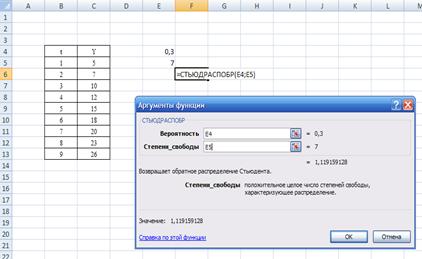
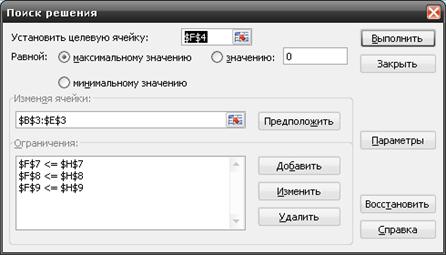
Воспользуемся функцией Excel СТЬЮДРАСПОБР. (рис. 4.10)
t = 1,12
Рис. 4.6
Для построения интервального прогноза рассчитаем доверительный интервал. Примем значение уровня значимости ![]() , следовательно, доверительная вероятность равна 70 %, а критерий Стьюдента при
, следовательно, доверительная вероятность равна 70 %, а критерий Стьюдента при ![]() равен 1,12.
равен 1,12.
Ширину доверительного интервала вычислим по формуле:
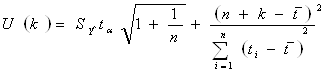 , где
, где
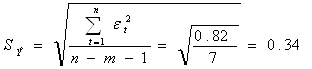
![]()
![]()
![]() (находим из таблицы 4.1)
(находим из таблицы 4.1)
![]() ,
,
![]() .
.
Вычисляем верхнюю и нижнюю границы прогноза (таб. 4.11).
Таблица 4.5
Таблица прогноза
| n +k | U (k) | Прогноз | Формула | Верхняя граница | Нижняя граница |
| 10 | U(1) =0.84 | 28.24 | Прогноз + U(1) | 29.сен | 27.40 |
| 11 | U(2) =1.02 | 30.87 | Прогноз - U(2) | 31.89 | 29.85 |
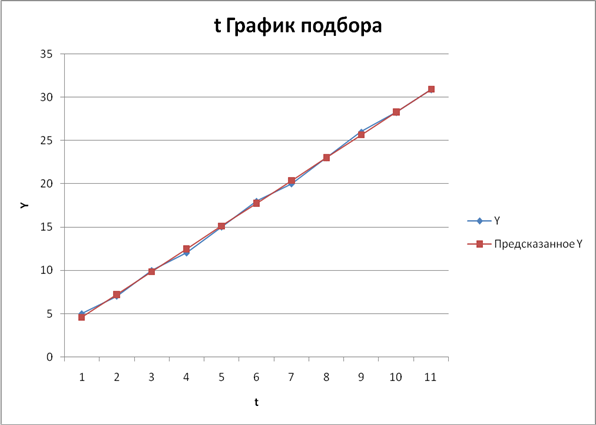
6) Фактические значения показателя, результаты моделирования и прогнозирования представить графически.
Преобразуем график подбора (рис. 4.5), дополнив его данными прогноза.
Рис. 4.7
Похожие работы
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
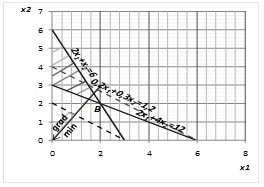
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...
... модели по тем свойствам, которые выбраны в качестве существенных (другими словами, должны быть произведены верификация и валидация модели). Применение численных результатов моделирования в экономике направлено на решение практических задач (анализ экономических объектов, экономическое прогнозирование развития хозяйственных и социальных процессов, выработка управленческих решений на всех уровнях ...
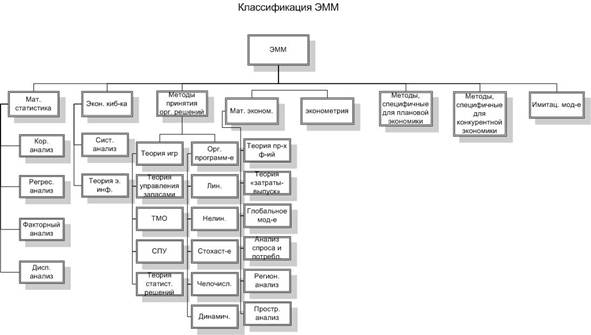
... , что найденный вариант является наилучшим. В современных условиях даже не значительные ошибки могут привести к огромным потерям. В связи с этим возникла необходимость привлечения к анализу и синтезу экономических систем оптимизационных экономико-математических методов и ЭВМ, что создает основу для принятия научно обоснованных решений. Такие методы объединяют в одну группу под общим названием « ...
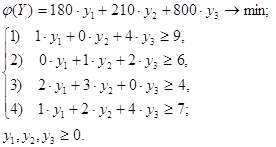
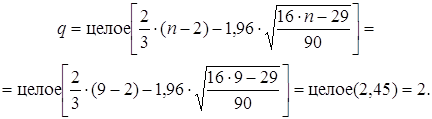


0 комментариев