Навигация
Выявление основной тенденции ряда динамики себестоимости продукции
5.3 Выявление основной тенденции ряда динамики себестоимости продукции
Выявим основную тенденцию развития ряда динамики. Построим ряд динамики помесячных значений себестоимости единицы продукции. За колебаниями ежемесячных значений может не просматриваться общая тенденция динамики, поэтому используем специальные методы.
-укрупнение интервалов
Рассматриваемый период разобьем на 8 интервалов равных кварталу (Приложение). Построим графики месячных и квартальных значений себестоимости единицы продукции (Рис 5.1).
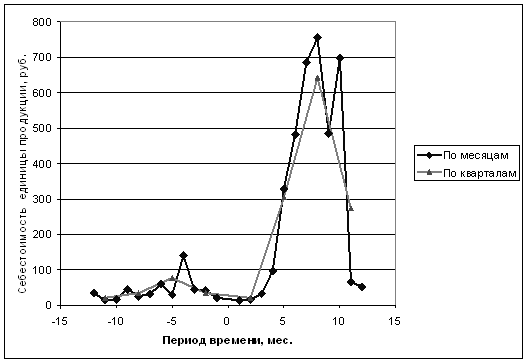
Рис. 5.1 - Динамика себестоимости единицы продукции
Полученная кривая отражает усредненную зависимость. По ней можно сделать общие выводы о динамике себестоимости единицы продукции. Значение увеличивается не равномерно, вопреки общей тенденции роста присутствуют снижения уровня себестоимости, в последнем периоде наметилось явное ее снижение, что может носить как локальный характер так и стать началом смены общей тенденции роста на тенденцию снижения себестоимости.
– метод скользящей средней;
Суть метода состоит в замене абсолютных месячных значений себестоимости средними арифметическими за определенные периоды. Расчет ведется способами скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Все расчеты приведены в таблице 2.
Таблица 2. Скользящие средние значения себестоимости единицы продукции
| Месяцы | Себестоимость продукции | Пятимесячные скользящие суммы | Пятимесячные скользящие средние | |
| январь | 32,90393013 | |||
| февраль | 13,1518847 | |||
| март | 16,45170732 | 26,48 | ||
| апрель | 44,99132112 | 26,25 | ||
| май | 24,90987984 | 132,41 | 35,35 | |
| июнь | 31,74208145 | 131,25 | 37,92 | |
| июль | 58,66874351 | 176,76 | 56,98 | |
| август | 29,27769572 | 189,59 | 60,65 | |
| сентябрь | 140,303653 | 284,90 | 62,47 | |
| октябрь | 43,24763705 | 303,24 | 54,72 | |
| ноябрь | 40,84312148 | 312,34 | 51,53 | |
| декабрь | 19,91136288 | 273,58 | 26,43 | |
| январь | 13,34939196 | 257,66 | 24,02 | |
| февраль | 14,80803571 | 132,16 | 35,28 | |
| март | 31,19151847 | 120,10 | 97,18 | |
| апрель | 97,141 | 176,40 | 191,14 | |
| май | 329,3873239 | 485,88 | 325,38 | |
| июнь | 483,1662198 | 955,69 | 470,28 | |
| июль | 686,0376176 | 1626,92 | 547,76 | |
| август | 755,6463878 | 2351,38 | 621,70 | |
| сентябрь | 484,5772871 | 2738,81 | 538,06 | |
| октябрь | 699,0557103 | 3108,48 | 411,19 | |
| ноябрь | 64,98900428 | 2690,31 | ||
| декабрь | 51,66256983 | 2055,93 |
По получившимся значениям построим графики по месячным значениям и по методу скользящей средней (Рис.5.2).
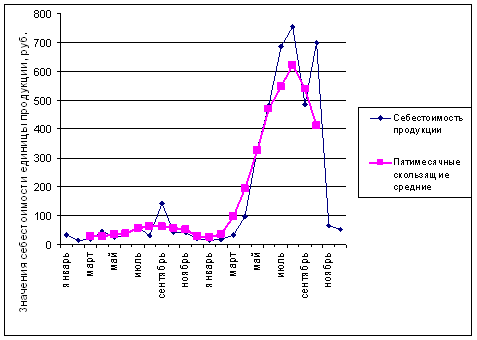
Рис.5.2 - Пятимесячные скользящие средние
По графику можно сделать выводы аналогичные выводам по методу укрупнения интервалов.
– метод аналитического выравнивания ряда динамики.
Для выравнивания ряда динамики по прямой используется следующие уравнение:
![]() .(5.18)
.(5.18)
Для нахождения параметров ![]() и
и ![]() по методу наименьших квадратов построим систему нормальных уравнений:
по методу наименьших квадратов построим систему нормальных уравнений:
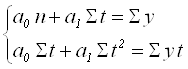 (5.19)
(5.19)
Где у – исходные уровни ряда динамики;
n – количество членов ряда;
t – показатель времени, который обозначается порядковыми номерами.
Если задать значения t таким образом, чтобы ![]() , т.е.
, т.е.
t = (…, -6, -4, -2, +2, +4, +6, …) , то система уравнений примет вид:
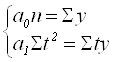 ,(5.20)
,(5.20)
тогда,
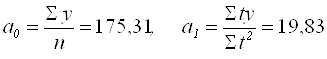 (5.21,5.22)
(5.21,5.22)
Таким образом, теоретическое уравнение ряда динамики примет вид:
![]() (5.23)
(5.23)
Построим прямую, описываемую данным уравнением (Рис.5.3):
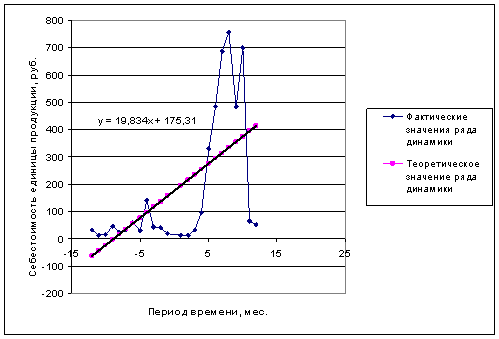
Рис.5.3 – Аналитическое выравнивание по прямой
Результаты полученные по данному методу так же свидетельствуют о тенденции повышения себестоимости единицы продукции.
Проведем оценку надежности уравнения динамики используя критерий Фишера:
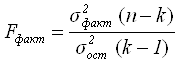 ,(5.24)
,(5.24)
Где ![]() – факторная дисперсия,
– факторная дисперсия,
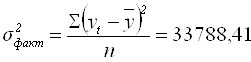 ;(5.25)
;(5.25)
![]() – остаточная дисперсия,
– остаточная дисперсия,
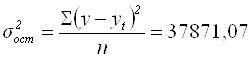 (5.26)
(5.26)
![]() – число параметров уравнения, описывающего основную тенденцию (для уравнения прямой
– число параметров уравнения, описывающего основную тенденцию (для уравнения прямой ![]() ), то есть
), то есть ![]() .
.
Сравним фактическое значение критерия Фишера с теоретическим (табличным). Табличное значение критерия Фишера равно:
| Fкр при | α=0,05 | 19,45 |
| α=0,01 | 99,46 |
Так как ![]() , следовательно уравнение динамики значимо, т.е. построенная модель адекватна фактической временной тенденции.
, следовательно уравнение динамики значимо, т.е. построенная модель адекватна фактической временной тенденции.
Основная тенденция показывает, как воздействуют систематические факторы на уровень ряда динамики.
Колеблемость уровней ряда около тренда служит мерой воздействия остаточных факторов. Найдем ее по формуле по формуле среднего квадратического отклонения:
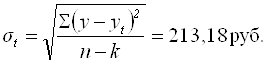 (5.27)
(5.27)
Относительной мерой колеблемости уровней эмпирического ряда относительно тренда является коэффициент вариации:
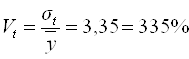 .(5.28)
.(5.28)
Колеблемость от теоретической прямой составляет 213,18 рублей или 335%. Так как коэффициент вариации много больше 30%, значения ряда динамики не однородны.
На основе аналитического выравнивания ряда выполним экстраполяцию себестоимости единицы продукции на следующий временной период, воспользовавшись уравнением динамики. При t=13 себестоимость единицы продукции:
![]()
При составлении прогноза оперируют интервальной оценкой, определяя доверительные интервалы прогноза. Величина доверительного интервала определяется:
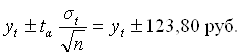 - при α=0,01;(5.29)
- при α=0,01;(5.29)
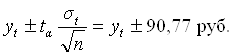 - при α=0,05.(5.30)
- при α=0,05.(5.30)
Где ![]() – среднее квадратическое отклонение от тренда;
– среднее квадратическое отклонение от тренда;
![]() – табличное значение t-критерия Стьюдента при уровне значимости
– табличное значение t-критерия Стьюдента при уровне значимости ![]() .
.
6. Исследование влияния факторов на себестоимость продукции
6.1 Выбор факторов, влияющих на себестоимость продукции графическим методом
Отберем факторы, которые на первый взгляд могут оказать влияние на себестоимость данной продукции: объём выпускаемой продукции, заработная плата (таблицы 6.1,6.2).
Построим корреляционные поля и линии тренда:
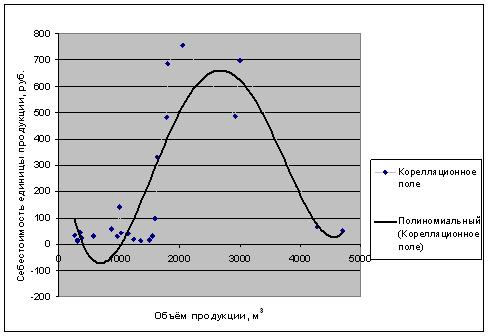
Рис.6.1 Зависимость себестоимости от объёма выпускаемой продукции
На рисунке видно, что себестоимость находится в полиноминальной зависимости от объёма выпускаемой продукции, на рисунке 6.2 – в экспоненциональной зависимости от заработной платы.
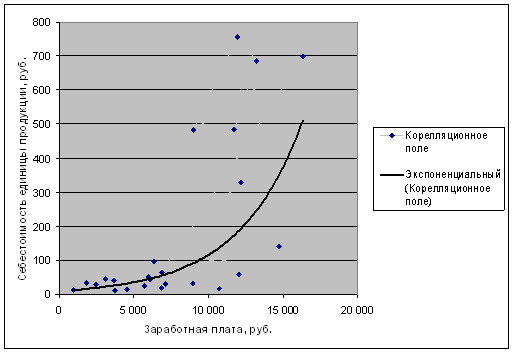
Рис.6.2 Зависимость себестоимости от заработной платы
0 комментариев