Навигация
В качестве факторного признака выберем заработная плата, тыс. руб
2. В качестве факторного признака выберем заработная плата, тыс. руб.
Таблица 6.3 Зависимость себестоимости от заработной платы
| Себестоимость, руб. | Заработная плата за единицу, тыс. руб. | |
| 13 | 943 | |
| 33 | 1 825 | |
| 29 | 2 417 | |
| 45 | 3 132 | |
| 41 | 3 647 | |
| 13 | 3 710 | |
| 15 | 4 528 | |
| 25 | 5 722 | |
| 52 | 6 010 | |
| 43 | 6 079 | |
| 97 | 6 314 | |
| 20 | 6 833 | |
| 65 | 6 915 | |
| 32 | 7 128 | |
| 31 | 8 928 | |
| 485 | 8 985 | |
| 16 | 10 740 | |
| 483 | 11 714 | |
| 756 | 11 918 | |
| 59 | 12 048 | |
| 329 | 12 161 | |
| 686 | 13 227 | |
| 140 | 14 720 | |
| 699 | 16 313 |
Примем количество интервалов для данной совокупности равным пяти и проведем аналитическую группировку. Результаты группировки представим в таблице 6.4.
Таблица 6.4 Аналитическая группировка себестоимости единицы продукции по заработной плате
| Группы по факторному признаку | Среднее значение себестоимости продукции в группе,
| Численность группы,
|
| 0-3506 | 25,11 | 4 |
| 3507-6312 | 31,47 | 6 |
| 6313-9119 | 121,59 | 6 |
| 9120-11925 | 418,42 | 3 |
| 1926-… | 382,69 | 5 |
Построим график групповых средних совместно с соответствующей эмпирической линией:

Рис.6.3 – Аналитическая группировка по заработной плате
Методика измерения тесноты связи в аналитической группировке вытекает из правила сложения дисперсий:
![]() .(6.1)
.(6.1)
Общая дисперсия характеризует вариацию результативного признака (у) от всех влияющих на него факторных признаков:
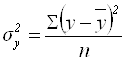 ,(6.2)
,(6.2)
где n – численность совокупности.
Групповые дисперсии и средняя из групповых характеризуют вариацию результативного признака у от всех факторных признаков, кроме признака х, по которому построена группировка:
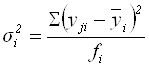 ;(6.3)
;(6.3)
 ,(6.4)
,(6.4)
гдеj – порядковый номер значения признака в i-й группе.
Межгрупповая дисперсия ![]() характеризует вариацию результативного признака от признака, положенного в основание группировки:
характеризует вариацию результативного признака от признака, положенного в основание группировки:
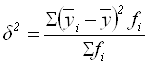 .(6.5)
.(6.5)
Отсюда можно получить относительный показатель – дисперсионное отношение – показывающий удельный вес вариации, связанной с группировочным признаком в общей дисперсии:
 .(6.6)
.(6.6)
Тесноту связи характеризует эмпирическое корреляционное отношение:
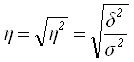 ; (6.7)
; (6.7)
![]() ,
,
![]() – связь слабая.
– связь слабая.
![]() – связь тесная.
– связь тесная.
Определив тесноту связи, необходимо убедиться, что связь эта не случайна, т.е. провести проверку существенности связи. Для этой цели может быть использован критерий Фишера (F – критерий):
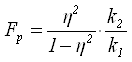 ,(6.8)
,(6.8)
![]() , (6.9)
, (6.9)
![]() ,(6.10)
,(6.10)
где ![]() – расчетное значение критерия Фишера;
– расчетное значение критерия Фишера;
n – число единиц совокупности;
m – количество групп.
Результаты расчетов по двум аналитическим группировкам сведем в таблицу 6.6:
Таблица 6.6 Расчет показателей по аналитическим группировкам
| Рассчитанные показатели | Номер интервала | Первая аналитическая группировка | Вторая аналитическая группировка |
| Среднее значение ряда распределения | 175,3089619 | 175,3089619 | |
| Внутригрупповая дисперсия | 1 | 20,84 | 25,11 |
| 2 | 33,88 | 31,47 | |
| 3 | 67,87 | 121,59 | |
| 4 | 24,70 | 418,42 | |
| 5 | 118,13 | 382,69 | |
| 6 | 641,62 | ||
| 7 | 325,07 | ||
| Дисперсия средняя из групповых | 17473,32 | 2067093908,66 | |
| Межгрупповая дисперсия | 21516,71 | 38296,30 | |
| Общая дисперсия | 71722,36 | 71722,36 | |
| Дисперсионное отношение | 0,31 | 0,53 | |
| Эмпирическое корреляционное отношение | 0,56 | 0,73 | |
| К1 | 6 | 4 | |
| К2 | 17 | 19 | |
| Fр | 8,79 | 5,44 | |
| Fкр | α=0,05 | 2,7 | 2,9 |
| α=0,01 | 4,1 | 4,5 |
При использовании объёма продукции в качестве факторного признака эмпирическое корреляционное отношение получаем равным 0,56, следовательно, в этом случае связь близка к тесной, для заработной платы - 0,76, связь тесная. Себестоимость единицы продукции на 31% зависит от объёма выпущенной продукции и на 58% от заработной платы. Обе связи не случайны, так как в обоих случаях Fр> Fкр. Таким образом, на себестоимость наибольшее влияние оказывает заработная плата.
0 комментариев