Навигация
Характеристика объекта проектирования и постановка задачи исследования
1. Характеристика объекта проектирования и постановка задачи исследования.
1.1 Схема и циклограмма дифференциального привода
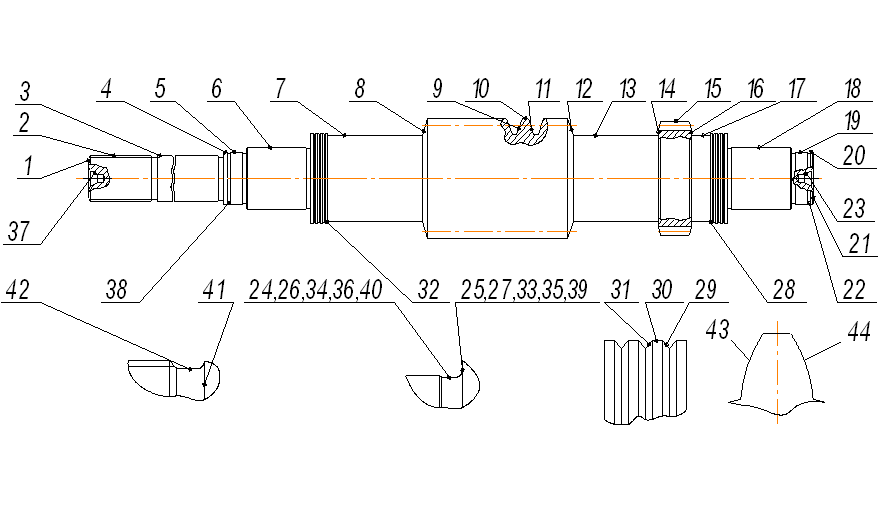
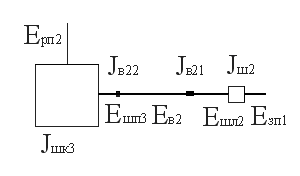
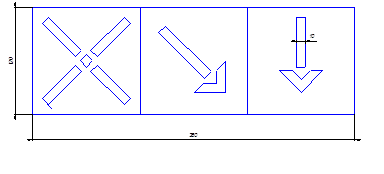
Схема одностороннего привода с дифференциальным поршнем 1, площади которого с обеих сторон значительно отличаются друг от друга, приведена на рис. 1. Штоковая полость привода постоянно соединена с магистралью (со сжатым воздухом давлением рм), а поршневая в исходном состоянии соединена с атмосферой (ра), благодаря чему создается начальный перепад давления сжатого воздуха, и поршень 1 занимает крайнее левое положение.
После срабатывания управляющего устройства 2 распределитель 3 сообщает с магистралью поршневую полость, давление воздуха в ней повышается, и когда сила давления со стороны этой полости превысит силу сопротивления привода, поршень начинает двигаться вправо (положение, показанное на рисунке). Как только поршень совершит свой рабочий ход s, управляющее устройство переключит распределитель 3, который соединит поршневую полость с атмосферой для того, чтобы поршень 1 мог вернуться в исходное состояние. Дроссели 4 и 5 служат для регулирования скорости движения поршня. Другие обозначения на чертеже будут объяснены позднее.

Рис. 1. Схема дифференциального привода
Односторонние приводы с начальным перепадом давления называют также дифференциальными. Рассмотрим последовательность действия этого привода, т. е. его циклограмму. В циклограмму пневмопривода кроме интервалов времени перемещения и остановки поршня для наглядности включены также интервалы времени изменения давления рl и р2 В полостях рабочего цилиндра в виде диаграммы (рис. 2).
Началом циклограммы является момент включения управляющего устройства, время срабатывания которого относится ко времени срабатывания распределителя (см. рис. 1). Процессы открытия отверстий для сжатого воздуха в управляющем устройстве и распределителе могут происходить одновременно с процессом распространения волны сжатого воздуха и заканчиваться в разные моменты времени.
В первом приближении предположим, что волна давления воздуха возникает после полного открытия отверстия распределителя, так как у большинства пневмоприводов время открытия распределителя невелико по сравнению с временем всего рабочего цикла.
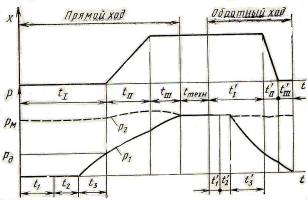
Рис. 2. Циклограмма дифференциального привода
Указанное допущение позволяет отдельно определять интервалы времени t1 (время открытия распределителя) и t2 (время распространения волны давления от распределителя до цилиндра, см. рис. 2). Горизонтальные прямые на верхней диаграмме соответствуют интервалам времени выстоев поршня, а наклонные - интервалам времени его движения. Кривые на нижней диаграмме отражают процессы изменения давлений рl и р2 воздуха соответственно в поршневой и штоковой полостях. Давление в первой из них начинает расти после открытия распределителя и этот процесс продолжается до начала движения поршня (давление рlд, интервал t3). Сумма интервалов t1, t2 и t3 составляет подготовительное время tІ.
В период движения поршня tІІ давление в этой полости может
монотонно увеличиваться (уменьшаться) или колебаться в зависимости от соотношения конструктивных параметров привода и нагрузки. В штоковой полости давление воздуха, равное магистральномy в исходном положении, при движении поршня несколько возрастает, в результате чего часть воздуха перетекает в магистраль, последний процесс может закончиться уже в период остановки поршня (штриховая линия). В поршневой полости после того, как поршень закончит рабочий ход, давление рl обычно уравнивается с магистральными рм или с давлением, требуемым технологическим процессом, которому соответствует время tтехн.
После выполнения заданной технологической операции управляющее устройство снова переключается (время tтехн технологической "операции не рассматривается). Затем в той же последовательности начинается обратный ход поршня, при этом вначале давление падает в обеих полостях: в поршневой - за счет соединения с атмосферой, а в штоковой - за счет увеличения ее объема при движении поршня влево. После возвращения поршня в исходное положение давление в поршневой полости падает до атмосферного, а в штоковой - поднимается до магистрального.
1.2 Процесс наполнения сжатым воздухом рабочей полости привода
Наполнение сжатым воздухом рабочей полости двигателя объемом V1 (см. рис. 1) происходит из магистрали, баллона или какого-либо другого источника питания, давление в котором принимаем постоянным (рм = const), имея в виду, что на входе в привод находится стабилизатор давления. Термодинамические процессы в пневматических приводах в первом приближении рассматриваем как квазистационарные и протекающие при установившихся режимах истечения.
При поступлении сжатого воздуха в полость рабочего цилиндра или при истечении из нее давление в различных точках объема будет неодинаковым. Сначала меняется давление вблизи входного (или выходного отверстия), затем изменение давления постепенно распространяется на весь объем.
Учитывая, что выравнивание параметров воздуха происходит достаточно быстро по сравнению с рассматриваемым процессом и большой разницы в их значениях для разных точек объема не наблюдается, в теории пневматических систем процессом выравнивания пренебрегают. Все процессы рассматривают как квазистационарные, т.е. такие, при которых во всех точках объема полости предполагаются одинаковые параметры (давление, температура и плотность). Принимаем, что рабочая полость имеет индекс 1.
Считая согласно первому закону термодинамики, что вся подведенная с газом тепловая энергия dQм расходуется на изменение внутренней энергии dU1 и на работу расширения газа dL1, запишем уравнение энергетического баланса
dQм = dU1 + dL1 (1.1)
Имея в виду, что количество тепловой энергии, поступившей в полость с газом, равно произведению его массы mм на удельную энтальпию (dQM = iMdmM), а внутренняя энергия U1 газа и совершаемая им работа L1 равны соответственно dU1 = d (u lml) и
dL1 = р1dV1,
представим уравнение (1.1) в следующем виде:
iM dmM = u ldml + ml dUl + рl dV1, (1.2)
где u l – удельная внутренняя энергия.
Выразим в уравнении (1.2) значения энтальпии и внутренней энергии через произведение температуры на теплоемкость соответственно при постоянных давлении ср и объеме сv:
сpTMdmM = сvTldml +cvmldTl + рldVl (1.3)
Рассматривая воздух как идеальный газ, молекулярными силами сцепления которого можно пренебречь, опишем его состояние с помощью уравнения Клапейрона:
рl V1= m1RT1, (1.4)
где R - газовая постоянная, R = 287 Дж/(кг, К) для воздуха (при Тм = 290 К).
Подставляя в уравнение (1.3) значение m1 dT1, полученное из уравнения (1.4), и полагая в нем ![]() и
и ![]() = R, где k - показатель адиабаты, после несложных преобразований получаем следующее выражение:
= R, где k - показатель адиабаты, после несложных преобразований получаем следующее выражение:
kRT м dmM = V1 dp1 + kp1 dV1.(1.5)
Заменим в уравнении (1.6) массу сжатого воздуха dmM, поступающего в полость V1 в течение времени dt, соответствующим значением GM расхода dmM = GM dt и выразим полученное уравнение относительно давления:
![]() (1.6)
(1.6)
Расход GM воздуха из неограниченного объема (магистрали) определяют чаще всего по формуле Сен-Венана и Ванцеля:
 , (1.7)
, (1.7)
где μ1 - коэффициент расхода;
f1 - площадь входного отверстия;
ТМ - температура воздуха в магистрали.
Из решения (1.5) совместно с уравнением (1.7) и определяют давление Р1 в полости как функцию времени. Из формулы (1.7) следует, что расход GM является функцией отношения давлений σ, в числителе которого всегда находится давление той среды, куда истекает газ, а в знаменателе - давление среды, откуда вытекает этот газ.
Представим формулу (1.7) расхода воздуха из магистрали σМ в более удобном виде:
![]() , (1.7)
, (1.7)
где ![]() ;
;
![]() ;
;
![]() .
.
При Т м = 293 К расход GM = 0,00912![]() , причем Рм в Па. Чтобы найти максимум расходной функции
, причем Рм в Па. Чтобы найти максимум расходной функции ![]() ер (а), приравняем нулю ее производную
ер (а), приравняем нулю ее производную ![]() , откуда получим, критическое отношение давлений
, откуда получим, критическое отношение давлений
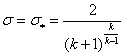 = 0,5282 (при к = 1,4). (1.9)
= 0,5282 (при к = 1,4). (1.9)
Подставим в уравнение (1.6) значение расхода GM из выражения (1.8), получим уравнение для определения давления в полости наполнения в общем виде:
![]() (1.10)
(1.10)
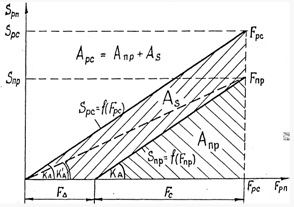
Объем V1 рабочей полости равен произведению площади поршня F1 на перемещение поршня х (с учетом его начальной координаты х01), т.е. ![]() . Подставим это значение в (1.10), получим
. Подставим это значение в (1.10), получим
![]() , (1.11)
, (1.11)
где ![]() ,
,
V01 - начальный объем рабочей плости,
F1 – площадь поршня.
Если это уравнение выразить относительно ![]() 1, то после интегрирования найдем время наполнения постоянного объема от начального безразмерного давления σ11 до заданного давления σ12:
1, то после интегрирования найдем время наполнения постоянного объема от начального безразмерного давления σ11 до заданного давления σ12:
![]() (1.12)
(1.12)
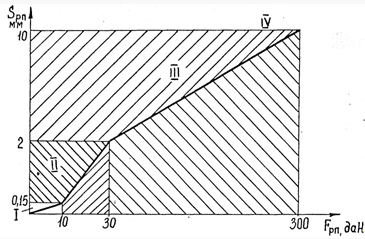
Значения функций Ψ1 (σ11) и Ψ1 (σ12) определяем по графику, приведенному на рис.3.
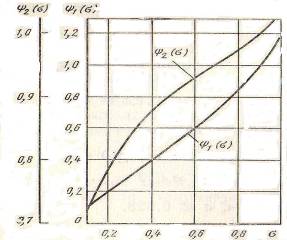
Рисунок 3
Формулу (1.13) применяют для определения времени наполнения полости постоянного объема до заданного давления, в том числе и для определения времени ![]() 3 (см. циклограмму на рис. 3).
3 (см. циклограмму на рис. 3).
Похожие работы
... : . (32) Производную (32) следует рассматривать как частную производную функции ряда переменных , одной из переменных - усилию в рулевом приводе автомобиля: . (33) Усилие в рулевом приводе, являющееся основной характеристикой рабочих процессов, в момент измерения критерия качества РП можно считать единственной переменной величиной, рассматривая остальные факторы постоянными, в ...
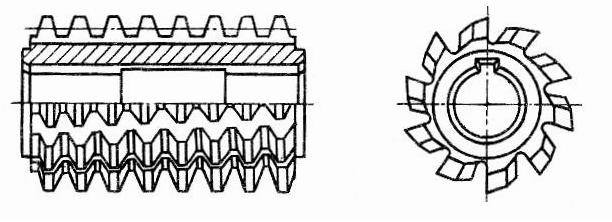
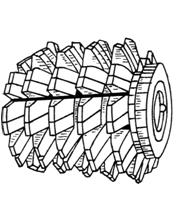
... 13.2 Идентификация опасных и вредных производственных факторов Проанализируем все опасные и вредные производственные факторы, которые могут возникнуть при выполнении технологических операций на участке изготовления червяка и внесем их в таблицу 13.2 Таблица 13.2 Опасные и вредные производственные факторы № п/п Наименование опасного и вредного производственного фактора Виды работ, ...
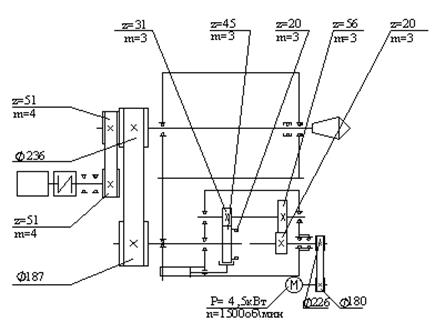
... двигателя и добиваемся его реализации путем изменения числа зубьев в приводе, сохраняя при этом общее число зубьев в сумме. На рисунке 1 приведена принципиальная кинематическая схема привода главного движения станка с учетом индивидуального задания, согласно которому общее передаточное отношение . Рисунок 1 – Кинематическая схема привода 1.1.2 Выбор двигателя Для выбора двигателя ...
... ситуациям. В связи с этим в настоящее время можно выделить две основные проблемы, связанные с совершенствованием автодромной подготовки водителей: - выбор рациональной конфигурации трассы автодрома и её параметров, исходя из конкретных задач обучения; - разработка технического оборудования автодромов, позволяющего моделировать различные дорожно-транспортные ситуации, в том числе и ...
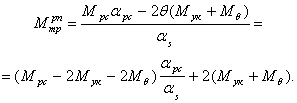
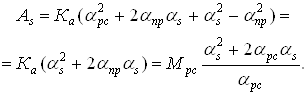
0 комментариев