Юридическая ответственность за нарушение нормативных требований по метрологии
Международная система единиц физических величин
Методы измерений
Средства измерений
Измерительные сигналы [5]
Классы точности средств измерений
Погрешность измерений
Причины возникновения погрешностей измерения
Планирование измерений
Обработка результатов наблюдений и оценивание погрешностей измерений [4]
Выбор измерительных средств по допустимой погрешности измерения
Выбор изметительных средств для других параметров [27]
Поверка средств измерений
Методы поверки (калибровки) и поверочные схемы [18]
Сертификация средств измерений
Государственный метрологический контроль и надзор
Права и обязанности государственных инспекторов по обеспечению единства измерений
Общие характеристики измерительных приборов
Цифровые измерительные приборы
Навигация
Погрешность измерений
Основы метрологии
186458
знаков
11
таблиц
8
изображений
3.5. Погрешность измерений
Погрешность измерений - это отклонение значений величины, найденной путём её измерения, от истинного (действительного) значения измеряемой величины.
Погрешность прибора - это разность между показанием прибора и истинным (действительным) значением измеряемой величины.
Разница между погрешностью измерения и погрешностью прибора заключается в том, что погрешность прибора связана с определёнными условиями его поверки.
Погрешность может быть абсолютной и относительной.
Абсолютной называют погрешность измерения, выраженную в тех же единицах, что и измеряемая величина. Например, 0,4В, 2,5мкм и т. д. Абсолютная погрешность
D = А – Хист » А – Хд,
где А - результат измерения; Xист - истинное значение измеряемой величины; Xд - действительное значение измеряемой величины.
Относительная погрешность измерения представляет собой отношение абсолютной погрешности измерения к истинному (действительному) значению измеряемой величины и выражается в процентах или долях измеряемой величины:
.
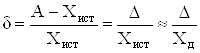В зависимости от условий измерения погрешности подразделяются на статические и динамические.
Статической называют погрешность, не зависящую от скорости изменения измеряемой величины во времени.
Динамической называют погрешность, зависящую от скорости изменения измеряемой величины во времени. Возникновение динамичесой погрешности обусловлено инерционностью элементов измерительной цепи средства измерений. Динамической погрешностью средства измерений является разность между погрешностью средства измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени.
3.5.1. Систематические и случайные погрешности
Систематической погрешностью называется погрешность, остающаяся постоянной или закономерно изменяющейся во времени при повторных измерениях одной и той же величины.
Примером систематической погрешности, закономерно изменяющейся во времени, может служить смещение настройки прибора во времени.
Случайной погрешностью измерения называется погрешность, которая при многократном измерении одного и того же значения не остаётся постоянной. Например, при измерении валика одним и тем же прибором в одном и том же сечении получаются различные значения измеренной величины.
Систематические и случайные погрешности чаще всего появляются одновременно.
Для выявления систематической погрешности производят многократные измерения образцовой меры и по полученным результатам определяют среднее значение размера. Отклонение среднего значения от размера образцовой меры характеризует систематическую погрешность. которую называют "средней арифметической погрешностью", или "средним арифметическим отклонением".
Систематическая погрешность всегда имеет знак отклонения, т.е. "+" или "-". Систематическая погрешность может быть исключена введением поправки.
При подготовке к точным измерениям необходимо убедиться в отсутствии постоянной систематической погрешности в данном ряду измерений. Для этого нужно повторить измерения, применив при этом уже другие средства измерения. По возможности нужно изменить и общую обстановку опыта - производить его в другом помещении, в другое время суток.
Прогрессивные и периодические систематические погрешности в противоположность постоянным можно обнаружить при многократных измерениях.
Обработка данных и оценка параметров случайных погрешностей производится методами математической статистики, изложенными в [42, 50].
При расчёте предельной погрешности измерения определяют числовое значение погрешности измерения от всех составляющих и производят суммирование:
,
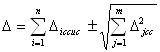где знаки "+" или "-" ставятся из условия, чтобы систематические и случайные погрешности суммировались по модулю.
Если в случайной погрешности известно среднее квадратическое отклонение, то
,
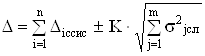где К - показатель, указывающий доверительные границы для предельной случайной погрешности измерения (при К=1 р=0,65; при К=2 р=0,945; при К=3 р=0,9973).
Если результаты измерений зависят от большого числа разнообразных факторов, то
y = F(x1, x2, …..xn) ,
где xi - переменные функциональные параметры.
Каждый параметр может иметь отклонение Dxi (погрешность) от предписанного значения xi. Поскольку погрешность Dxi мала по сравнению с величиной xi, суммарная погрешность Dy функции y можно вычислять по формуле 
, (3.1)
где ¶y/¶xi - передаточное отношение (коэффициент влияния) параметра xi.
Формула (3.1) справедлива лишь для систематических погрешностей Dxi.
Для случайных погрешностей (когда отдельные составляющие не всегда принимают предельные значения) используются теоремы теории вероятностей о дисперсии, то есть
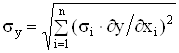. (3.2)
Суммарная погрешность при наличии только случайных составляющих dxi погрешностей
,
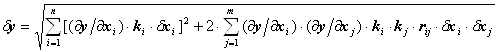где m - число попарно корреляционно связанных параметров;
ki и kj - коэффициенты относительного рассеяния, характеризующие степень отличия закона распределения погрешности данного параметра от нормального;
rij - коэффициент корреляции, существующий при наличии корреляционной связи между параметрами xi и xj.
При наличии и систематических и случайных составляющих погрешностей вычисляют доверительные границы суммарной погрешности:
Dyсум = Dy ± k×sy ,
где k - масштабный коэффициент интервала распределения, зависящий от закона распределения и принятой доверительной вероятности. Так, при доверительной вероятности Р = 0,95 для закона нормального распределения k = 2, а для закона Максвелла k = 3,6.
Пример. В результате измерений и последующего вычисления по формуле (3.1) получена суммарная систематическая погрешность результата измерения Dy =
-0,7 мкм, среднее квадратическое этого результата измерения, вычисленное по формуле (3.2) sy = 0,4 мкм. При доверительной вероятности Р =0,95 предел допускаемой погрешности dизм = +1 мкм. Тогда верхняя и нижняя доверительные границы погрешности
Dyсум в = -0,7 + 2×0,4 = +0,1 мкм; Dyсум н = -0,7 - 2×0,4 = -1,5 мкм.
Так как Dyсум н > dизм , выбранный метод и средство измерения не удовлетворяют требованиям точности. Следовательно, необходимо скомпенсировать систематическую составляющую погрешности, например, путём изготовления образца для настройки измерительного средства. Размер образца должен быть больше его начального размера на 0,7 мкм; тогда будет справедливо неравенство 0,8 < 1 мкм и проведённые измерения будут удовлетворять требованиям по точности.
Похожие работы
... фахівцями, в обов'язки яких не входить аналіз похибок результатів вимірювання. Для забезпечення необхідного рівня точності технічних вимірювань при їхньому виконанні користуються атестованими методиками виконання вимірювань, які розробляють висококваліфіковані спеціалісти - метрологи. Вимірювання ФВ за наявністю або відсутністю розмірності у вимірюваних величин поділяють на вимірювання розмірних ...
... , которые могут использовать возможности и преимущества стандартизации и сертификации в качестве весомых составляющих конкурентоспособности товара. 1. Предмет, задачи и структура дисциплины «Правовые основы метрологии, стандартизации, сертификации» Стандартизация, сертификация и метрология в том виде, как это было в плановой экономике, не только не вписывались в новые условия работы, но и ...
дать общие сведения о взаимозаменяемости и ее размерной составляющей, о размерах и допусках на размер, о различных характерах соединений деталей и способах их обеспечения; дать основные понятия в области стандартизации, ее нормативных документах, о стандартизации в различных сферах деятельности человека. Цель контрольной работы – изучить основные понятия и опреределения в области метрологии, ...
... . Може мати реперні точки. Позитивні та негативні значення. Методи вимірювання – прямі, опосередковані; зіставлення, протиставлення, порівняння з мірою, компенсаційні, накладання. Основними задачами прикладної метрології є: - розробка та виробництво засобів вимірювальної техніки (ЗВТ); - застосування ЗВТ; - повірка (калібрування, атестація, випробування) ЗВТ; - розробка методик виконання вим ...
0 комментариев