Навигация
Определение исходных данных
1.2 Определение исходных данных
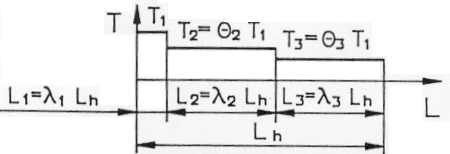
Определение длительности действия max нагрузок
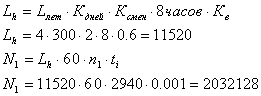
Так как N1>5*104 => первая передача рассчитывается на усталость с 1 – го участка диаграммы нагружения
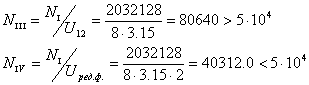
Определение вращающих моментов



Определяем расчетные вращающие моменты
Так как NI и NIIв результате расчетов превышают 5*104 , то ![]()
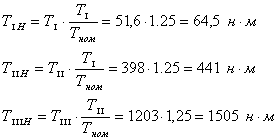
Соответственно так как на NIVне превышают 5*104 , то ![]()
![]()
2 РАСЧЕТ ЗУБЧАТЫХ ПЕРЕДАЧ
Cогласно [2, с.11, табл. 1.2]
Таблица 2.1
| Вид ХТО | Твердость зуба | σFlim, МПа | σHlim, МПа | [σF], МПа | [σH], МПа | Марка ст. ГОСТ |
| Закалка ТВЧ | 53 HRC | 650 | 1100 | 260 | 825 | 40 ХН 4543-71 |
Область применения: редукторы общего назначения в серийном и массовом производстве.
Требования к габаритам – жесткие. Материал зубьев (марка стали) – 40, 45, 40Х, 40ХН. [2, с.15, табл.1.4]
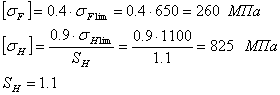
2.1 Расчет цилиндрических передач
2.1.1 Приближенный проектировочный расчет главного и основного параметров передач из условия обеспечения контактной прочности зубьев
Выполняется для колес с твердостью рабочих поверхностей зубьев более 350 НВ в следующем порядке. [2, с.22, 23]. Расчет первой передачи проводится в ручную, второй и третьей – с помощью модуля автоматизированного проектирования цилиндрических передач на базе программы Microsoft Excel.
Выбирается число зубьев шестерни
Z1 (для шевронной передачи – в интервале 13…25
для косозубой передачи – в интервале 16…25
для прямозубой передачи – в интервале 17…25 )
Z2= Z1*U, где U – передаточное число соответствующей ступени
Предварительно принимается угол наклона зубьев
β (для шевронной передачи – в интервале 25°…40°
для косозубой передачи – в интервале 8°…17°)
Рассчитывается минимальное значение модуля зацепления в мм, при котором обеспечивается изгибная прочность зубьев колеса цилиндрической передачи, определяется по следующей формуле
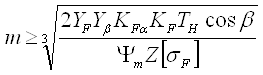
где ![]() - коэффициент, учитывающий форму зуба и концентрацию напряжений, выбирается из [2, табл. 1.5] по эквивалентному числу зубьев ZV=Z/cos β
- коэффициент, учитывающий форму зуба и концентрацию напряжений, выбирается из [2, табл. 1.5] по эквивалентному числу зубьев ZV=Z/cos β
![]() - коэффициент, учитывающий угол наклона зуба, находится по следующей зависимости:
- коэффициент, учитывающий угол наклона зуба, находится по следующей зависимости:
![]() ;
;
![]()
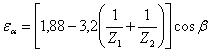
![]() - коэффициент, учитывающий неравномерность нагрузки по длине зуба, принимается предварительно равным 1,5;
- коэффициент, учитывающий неравномерность нагрузки по длине зуба, принимается предварительно равным 1,5;
![]() - вращающий момент на соответствующем валу;
- вращающий момент на соответствующем валу;
![]() - отношение ширины зубчатого венца к нормальному модулю;
- отношение ширины зубчатого венца к нормальному модулю;
![]() - допускаемые изгибные напряжения зубчатого колеса.
- допускаемые изгибные напряжения зубчатого колеса.
В формулу расчета модуля зацепления подставляются значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() того элемента (шестерни или колеса), у которого соотношение
того элемента (шестерни или колеса), у которого соотношение ![]() /
/![]() меньше. В данном проекте расчет всех передач проводился по элементу «шестерня», согласно вышеизложенному материалу.
меньше. В данном проекте расчет всех передач проводился по элементу «шестерня», согласно вышеизложенному материалу.
Расчетное значение модуля необходимо округлить до ближайшего большего стандартизованного значения [2, табл.1.6].
Дальнейший расчет сводится к вычислению межосевого расстояния
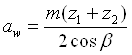
а также уточнению фактического значения угла наклона зубьев
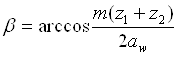
Основные размеры колес определяют по формулам:
Делительный диаметр колес: 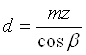
Диаметр окружностей впадин: ![]()
Диаметр окужностей выступов: ![]()
Межосевое расстояние: 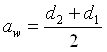
Ширина зубчатого венца: ![]()
Расчет первой передачи (шевронная передача)
| Вращающий момент на шестерне | Тн, Н/мм | 64,5 |
| Число зубьев шестерни | Z1 | 18 |
| Передаточное число передачи | U | 8 |
| Определение числа зубев колеса Z2 | 144 | |
| Расчетное значение модуля m, мм | 2,150691 | |
| Выбранный коэффициент YF | 4,12 | |
| Допускаемые напряжения σF, Мпа | 260 | |
| Эквивалентное число зубьев шестерни ZV | 24,69 | |
| Предварительно принятый угол наклона зуба β° | 30 | |
| Коэффициент Yβ | 0,815429 | |
| Коэффициент KFα | 0,636585 | |
| Коэффициент εα | 1,727971 | |
| Коэффициент нагрузки KF | 1,5 | |
| Отношение Ψm | 18 | |
| Принятое значения модуля | m | 2 |
| Межосевое расстояние | aw= | 180 |
| Уточненнное значение угла наклона зуба | beta | 25,84 |
| Делительный диаметр шестерни | d1= | 40 |
| Делительный диаметр колеса | d2= | 320 |
| Диаметр впадин шестерни | df1= | 35 |
| Диаметр впадин колеса | df2= | 315 |
| Диаметр выступов шестерни | da1= | 44 |
| Диаметр выступов колеса | da2= | 324 |
Расчет второй передачи (косозубая передача)
| Вращающий момент на шестерне | Тн, Н/мм | 441 |
| Число зубьев шестерни | Z1 | 24 |
| Передаточное число передачи | U | 3,15 |
| Определение числа зубев колеса Z2 | 76 | |
| Расчетное значение модуля m, мм | 4,190781 | |
| Выбранный коэффициент YF | 3,85 | |
| Допускаемые напряжения σF, Мпа | 260 | |
| Эквивалентное число зубьев шестерни ZV | 25,64 | |
| Предварительно принятый угол наклона зуба β° | 12,00 | |
| Коэффициент Yβ | 0,914286 | |
| Коэффициент KFα | 0,635189 | |
| Коэффициент εα | 1,731767 | |
| Коэффициент нагрузки KF | 1,5 | |
| Отношение Ψm | 10 | |
| Принятое значения модуля | m= | 5 |
| Межосевое расстояние | aw= | 260 |
| Уточненнное значение угла наклона зуба | beta | 16,73 |
| Делительный диаметр шестерни | d1= | 125,3012 |
| Делительный диаметр колеса | d2= | 394,6988 |
| Диаметр впадин шестерни | df1= | 112,8012 |
| Диаметр впадин колеса | df2= | 382,1988 |
| Диаметр выступов шестерни | da1= | 135,3012 |
| Диаметр выступов колеса | da2= | 404,6988 |
Расчет третьей передачи (прямозубая передача)
| Вращающий момент на шестерне | Тн, Н/мм | 1505 |
| Число зубьев шестерни | Z1 | 21 |
| Передаточное число передачи | U | 2 |
| Определение числа зубев колеса Z2 | 42 | |
| Расчетное значение модуля m, мм | 7,568309 | |
| Выбранный коэффициент YF | 4,12 | |
| Допускаемые напряжения σF, Мпа | 260 | |
| Эквивалентное число зубьев шестерни ZV | 21,00 | |
| Угол наклона зуба β° | 0,00 | |
| Коэффициент Yβ | 1 | |
| Коэффициент KFα | 0,66609 | |
| Коэффициент εα | 1,651429 | |
| Коэффициент нагрузки KF | 1,5 | |
| Отношение Ψm | 8 | |
| Принятое значения модуля | m | 8 |
| Межосевое расстояние | aw= | 250 |
| Делительный диаметр шестерни | d1= | 166,6667 |
| Делительный диаметр колеса | d2= | 333,3333 |
| Диаметр впадин шестерни | df1= | 146,6667 |
| Диаметр впадин колеса | df2= | 313,3333 |
| Диаметр выступов шестерни | da1= | 182,6667 |
| Диаметр выступов колеса | da2= | 349,3333 |
Сведем расчетные данные в таблицу 2.2
Таблица 2.2
| Передача 1 | Передача 2 | Передача 3 | |||
| z1 | 18 | 24 | 21 | ||
| U | 8 | 3,15 | 2 | ||
| z2 | 144 | 75,60 | 42 | ||
| m | 2 | 5 | 8 | ||
| aw | 180 | 260 | 250 | ||
| d1 | 40 | 125,3012 | 166,6667 | ||
| d2 | 320 | 394,6988 | 333,3333 | ||
| da1 | 44 | 135,3012 | 182,6667 | ||
| da2 | 324 | 404,6988 | 349,3333 | ||
| df1 | 35 | 112,8012 | 146,6667 | ||
| df2 | 315 | 382,1988 | 313,3333 | ||
| beta | 25,84193 | 16,72594 | 0 | ||
| bw1 | 75 | 50 | 71 | ||
| bw2 | 70 | 45 | 64 |
Похожие работы
... с односторонним расположением губок для измерения наружных и внутренних размеров. При измерении поверхности микрометра приводятся в соприкосновение с поверхностями изделия. За результат измерения принимается алгебраическая сумма отсчетов по шкалам микрометра. 7.2 Расчет размеров калибров для гладкого цилиндрического соединения Калибры применяют не для определения числового значения ...
... *0,72*0,992=3,764 кВт; Р4=Р3 η3=5,124*0,95=3,576 кВт, что близко к заданному. Определяем вращающие моменты на каждом валу привода по формуле (Нм) (2.5) ; ; ; . Все рассчитанные параметры сводим в табл.1. Таблица 1 Параметры кинематического расчета № вала n, об/мин ω, рад/с Р, кВт Т, Нм U Дв. (1) 1444,5 151,27 5,5 36,35 2 ...
... = 60 ґ n ґ Lh / 106 L = 60 ґ 1435 ґ 100000 / 106 = 861 7.1.9. Определяю расчетную динамику подшипника c = PIIпр3.3 z c = 1222.16 3.3 861 = 9473.77 Основные характеристики принятого подшипника: Подшипник № 36205 d = 25мм D = 52мм C = 16700H = 15мм r = 1.5мм C0 = 9100H n = 13000 об/мин 7.2. Проектный расчет второго вала редуктора и подбор подшипников d2 = c 3 ...
... w и Т заносятся в таблицу 3.1. Примечание. Для одноступенчатого редуктора крутящий момент определяется по формуле , [Н·м]; , [Н·м]; [Н·м]; , [Н·м]. [Н·м]. Расчет клиноременной передачи Расчет клиноременной передачи проводим исходя из ранее рассчитанной мощности электродвигателя, Рэд и принятого передаточного отношения клиноременной передачи iр.п.=2. Определение сечения ремня ...
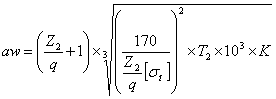

0 комментариев