Навигация
Исследовать ряд на сходимость
4395
знаков
0
таблиц
9
изображений
3. Исследовать ряд на сходимость
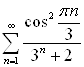
Решение.
Так как 
, то рассмотрим ряд
, тогда
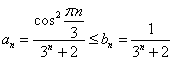
Воспользуемся признаком Даламбера.
, 
Тогда,
Так как 
, то ряд сходится. Значит, исходный ряд 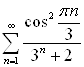сходится по теореме о сравнении рядов.
Ответ: Ряд 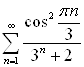сходится.
4. Исследовать ряд на сходимость
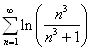
Решение.
Преобразуем n – член этого ряда.
Сравним ряд 
с рядом 
, пользуясь предельным признаком сравнения:
, 
Тогда,
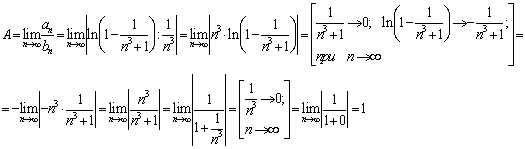
Поскольку А = 1 (0<A<+∞) – действительное число. Следовательно, ряды либо сходятся, либо расходятся. Ряд - является рядом Дирихле. Так как α = 3 > 1, то данный ряд сходится. Следовательно, и сравниваемый ряд 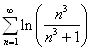тоже сходится.
Ответ: ряд 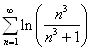сходится.
5. Исследовать ряд на сходимость
Решение.
Воспользуемся признаком Даламбера.
, 
Находим m по формуле:
Тогда:
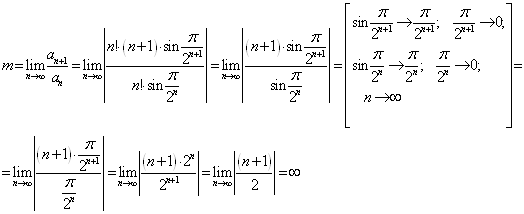
Так как 
, то ряд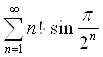 
расходится.
Ответ: ряд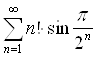 
расходится.
6. Исследовать ряд на сходимость
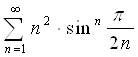
Решение.
Рассмотрим ряд
.
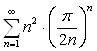Поскольку 
при 
:
Воспользуемся признаком Даламбера.
,
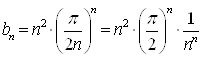
Находим m по формуле:
Тогда:
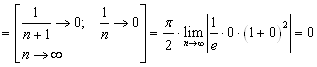
Так как 
, то ряд 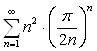сходится.
Согласно признаку сравнения сходится и ряд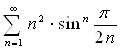 
.
Ответ: ряд 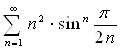сходится.
7. Вычислить сумму ряда с точностью α..
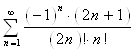α. = 0,001.
Решение.
Прежде чем находить сумму ряда необходимо убедиться, что данный ряд сходится. Проверим исходный ряд на сходимость.
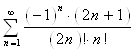- числовой знакочередующейся.
Воспользуемся признаком Лейбница:
1) 
2) 
Следовательно, ряд 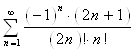условно сходится.
Проверим абсолютную сходимость ряда 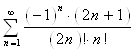. Рассмотрим ряд 
.
Воспользуемся признаком Даламбера:
, 
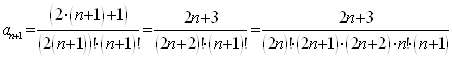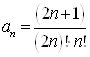
Находим m по формуле:
Тогда:
Следовательно, ряд
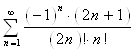сходится абсолютно.
Вычисляем члены ряда с точностью до 4 цифр после запятой до тех пор, пока какой-нибудь член ряда по модулю не будет меньше α. = 0,001:
а1 = -1,5 а2 = 0,1042 а3 = - 0,0016 а4 = 0,0000093
Для приближённого вычисления ряда достаточно первых трех членов ряда (по следствию признака Лейбница: сумма сходящегося знакопеременного числового ряда не превышает его первого члена). Следовательно, ошибка при вычислении не превысит 0,0000093, а, значит, и 
. Требуемая точность достигнута.
Следовательно:
.
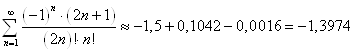Ответ: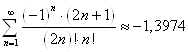 
.
Похожие работы
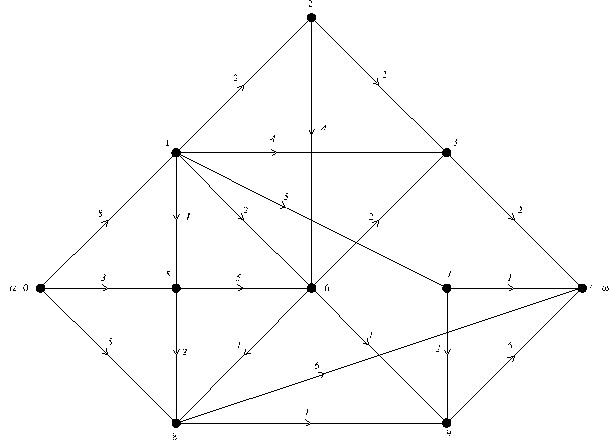
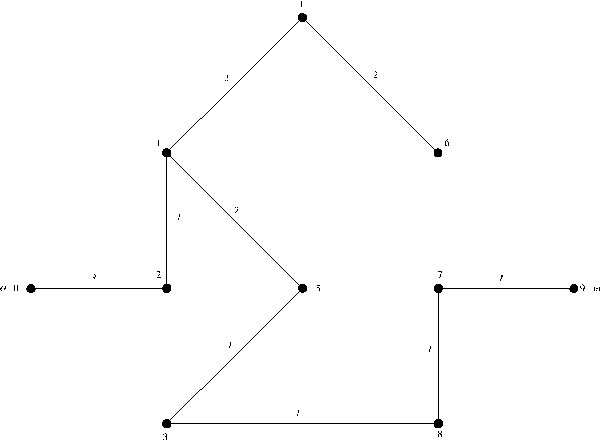
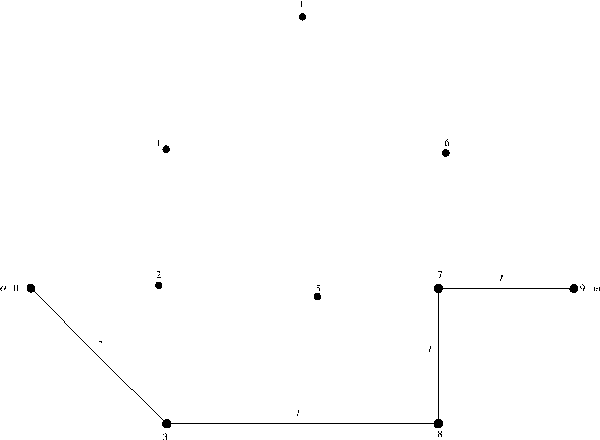
... vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок. Матрица весов двудольного графа K55 : y1 y2 y3 y4 y5 x1 2 0 0 0 0 x2 0 7 9 8 6 x3 0 1 3 2 2 x4 0 8 7 6 4 x5 0 7 6 8 3 Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах. Второй этап - ...
... в каждом конкретном случае исходя из габаритов проектируемого технического оборудования, места расположения насосной станции и рабочих органов машины, способов монтажа гидрооборудования и других условий. Для технологического оборудования малых и средних типоразмеров можно принять длины участков в следующих пределах: всасывающий трубопровод- до 1 метра, напорный и сливной до 5 метров. Для ...
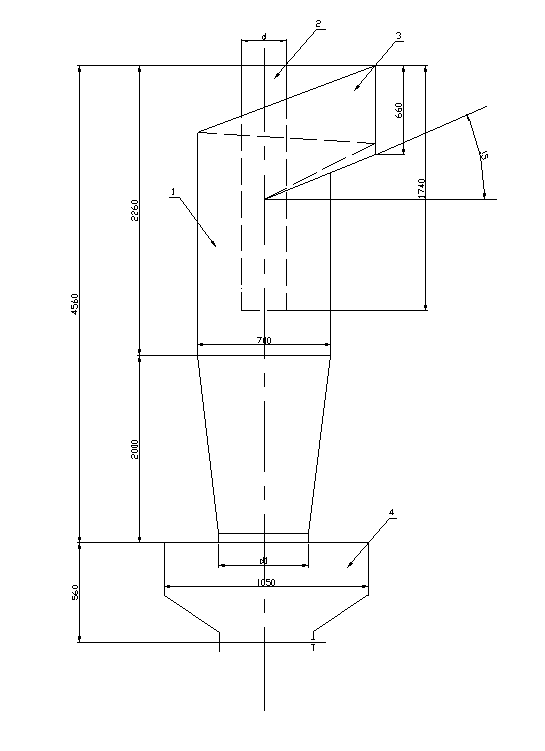
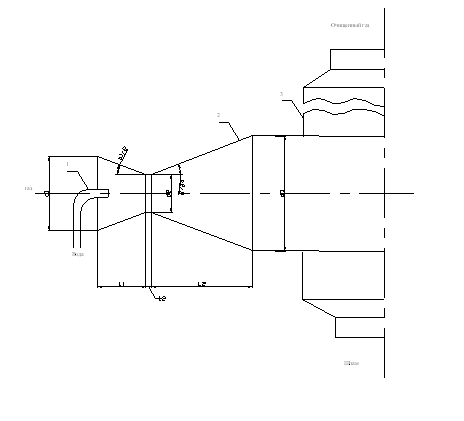
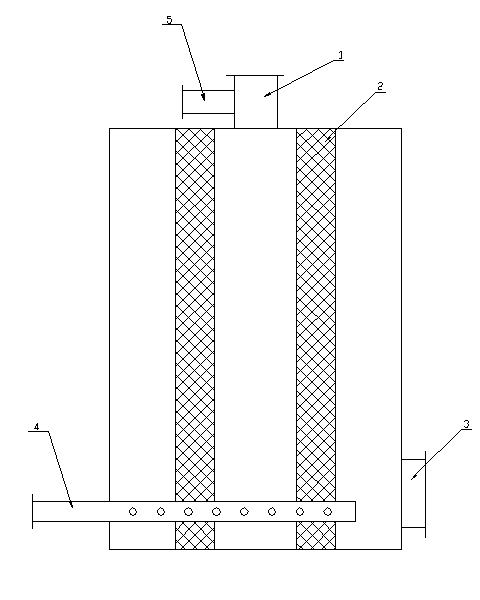
... м3/с Vг = Мг/rг = 0,9/0,9 = 1 м3/с Кт = 10662855 + 300×103(8,65×10-4/1) = 10663114 Па Определяем эффективность скруббера Вентури Эффективность скруббера Вентури, полученная в результате расчетов (величина ), удовлетворяет заданному условию, т.е. обеспечивает очистку газов от пыли с эффективностью не менее 0.9. Рис. 2.1 Скруббер Вентури 1 – форсунки 2 – сопло 3 – ...
... нефтепровода, м 25 ρ - средняя плотность, т/м3 0,870 P1 - давление насосной станции, кгс/см2 46 P2 - давление в конце участка, кгс/см2 1,5 δ - толщина стенки, мм 14 Таблица 2 - Данные для прочностного расчета Параметры Вариант 3 Dн - диаметр трубопровода наружный, мм 1220 Марка стали 12 Г2СБ t0 - температура при сварке замыкающего стыка, 0с ...
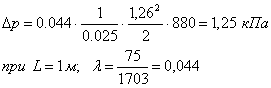
0 комментариев