Навигация
Монета бросается до тех пор, пока герб не выпадет n раз. Определить вероятность того, что решка выпадает m раз
11. Монета бросается до тех пор, пока герб не выпадет n раз. Определить вероятность того, что решка выпадает m раз.
Дано: n = 5, m = 3.
Решение.
Испытание состоит в бросании монеты.
Вероятность выпадения решки в каждом испытании постоянна: р = 0,5 , а выпадения герба – q = 1 – p = 1 -0,5 = 0,5. Всего монета бросается (n + m) = 5 + 3= 8 раз. Следовательно, указанный эксперимент удовлетворяет схеме Бернулли. Тогда искомую вероятность находим по формуле:
![]()
Отсюда, искомая вероятность равна:
![]()
Ответ: 0,2187.
12. На каждый лотерейный билет с вероятностью р1 может выпасть крупный выигрыш, с вероятностью р2 – мелкий выигрыш, и с вероятностью р3 билет может оказаться без выигрыша ![]() . Куплено n билетов.
. Куплено n билетов.
Определить вероятность получения n1 крупных выигрышей и n2 мелких.
Дано: n = 14, n1 = 2, n2 = 4, р1 = 0,2, р2 = 0,2.
Решение.
Событие А – среди 14 билетов получено 2 крупных выигрыша и 4 мелких.
Рассмотрим события:
Событие А1 – выпал крупный выигрыш.
Событие А2 – выпал мелкий выигрыш.
Событие А3 – билет оказался без выигрыша.
Вероятности этих событий соответственно равны: р1 = 0,2, р2 = 0,2, р3 = 1 - 0,2 – 0,2 = 0,6.
Вероятность события А находим по формуле полиномиального распределения вероятностей:
![]()
Отсюда:
![]()
Ответ: ![]() .
.
13. Вероятность наступления некоторого события в каждом из n независимых испытаний равна р .
Определить вероятность того, что число m наступлений событий удовлетворяет следующему неравенству: k1 ≤ m.
Дано:n = 100, p = 0,8, k1 = 70.
Решение.
Воспользуемся интегральной теоремой Лапласа:
![]() ,
,
где: Ф(х) – функция Лапласа,
![]() ,
,![]()
По условию, n=100, p= 0,8, q = 1- p = 1- 0,8 = 0,2 , k1 = 70, k2 = 100. Вычислим х` и x``:
![]()
![]() ,
, ![]()
![]()
Учитывая, что функция Лапласа нечетна, то есть Ф(-х) = - Ф(х), получим
![]()
По таблице приложения 2 найдем: Ф(5) = 0,5; Ф(2,5)= 0,4938.
Искомая вероятность равна:
Р100(![]() ) = 0,5 + 0,4938 = 0,9938.
) = 0,5 + 0,4938 = 0,9938.
Ответ: 0,9938.
14. Дана плотность распределения 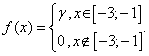 случайной величины Х.
случайной величины Х.
Найти параметр γ, функцию распределения ![]() случайной величины Х. математическое ожидание М(х), дисперсию D(x), вероятность выполнения неравенства -2< x < 0.
случайной величины Х. математическое ожидание М(х), дисперсию D(x), вероятность выполнения неравенства -2< x < 0.
Решение.
Воспользуемся свойством плотности распределения:
![]() .
.
В данном случае:
![]() , так как
, так как ![]() при
при ![]() . Тогда:
. Тогда:
![]()
То есть: ![]()
Тогда получим две функции плотности распределения:

Контроль:
![]()
Функцию распределения ![]() случайной непрерывной величины Х найдём по формуле:
случайной непрерывной величины Х найдём по формуле:
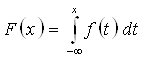
где: ![]() - функция плотности распределения вероятностей на трёх интервалах.
- функция плотности распределения вероятностей на трёх интервалах.
1) При ![]() имеем:
имеем:
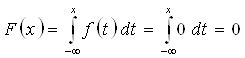
2) При ![]() исходный интеграл разобьем на два интеграла:
исходный интеграл разобьем на два интеграла:
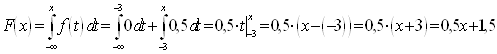
3) При ![]() исходный интеграл разобьем на три интеграла:
исходный интеграл разобьем на три интеграла:
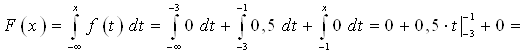
![]()
Таким образом, функция распределения ![]() примет вид:
примет вид:

б) Математическое ожидание находим по формуле:
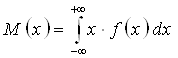
Применяя формулу, получим:

в) Найдём дисперсию случайной величины Х :
![]()
Найдём математическое ожидание квадрата случайной величины Х по формуле:
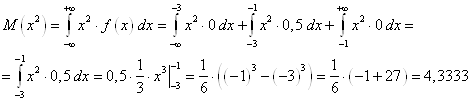
Тогда дисперсия
![]()
Определяем вероятность выполнения неравенства -2 < x < 0:
![]()
Ответ:
![]() ,
, 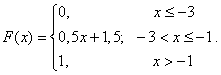
М(х) = -2, D(x) = 0,3333, ![]() .
.
Похожие работы
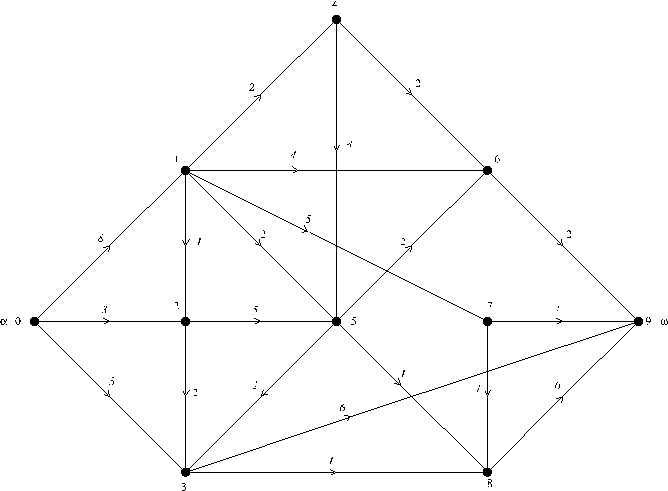
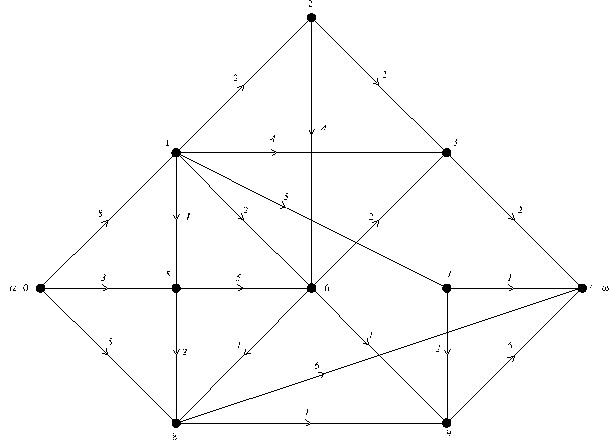
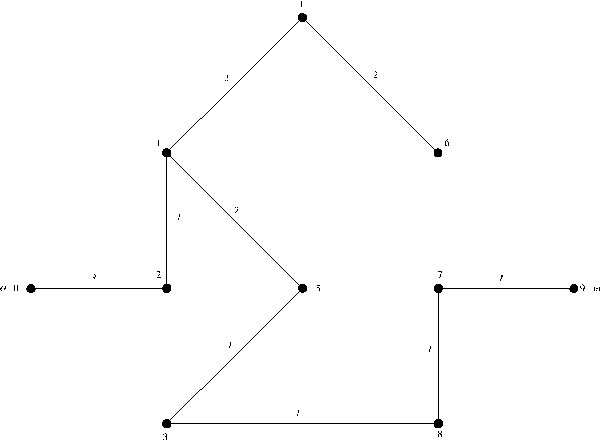
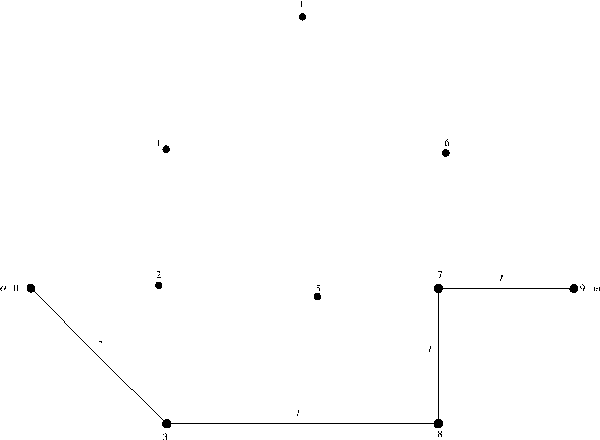
... vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок. Матрица весов двудольного графа K55 : y1 y2 y3 y4 y5 x1 2 0 0 0 0 x2 0 7 9 8 6 x3 0 1 3 2 2 x4 0 8 7 6 4 x5 0 7 6 8 3 Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах. Второй этап - ...
... в каждом конкретном случае исходя из габаритов проектируемого технического оборудования, места расположения насосной станции и рабочих органов машины, способов монтажа гидрооборудования и других условий. Для технологического оборудования малых и средних типоразмеров можно принять длины участков в следующих пределах: всасывающий трубопровод- до 1 метра, напорный и сливной до 5 метров. Для ...
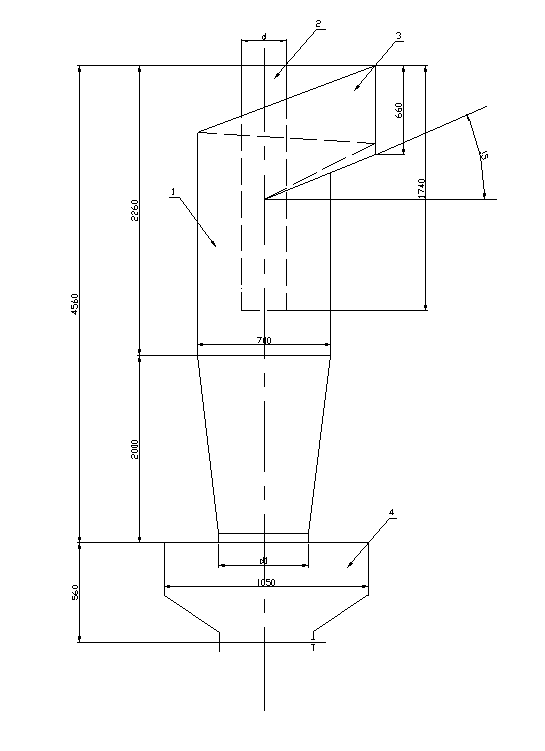
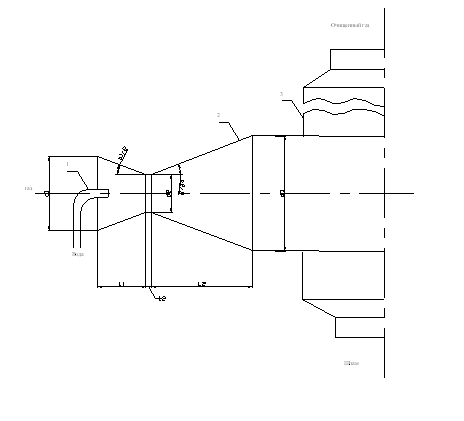
... м3/с Vг = Мг/rг = 0,9/0,9 = 1 м3/с Кт = 10662855 + 300×103(8,65×10-4/1) = 10663114 Па Определяем эффективность скруббера Вентури Эффективность скруббера Вентури, полученная в результате расчетов (величина ), удовлетворяет заданному условию, т.е. обеспечивает очистку газов от пыли с эффективностью не менее 0.9. Рис. 2.1 Скруббер Вентури 1 – форсунки 2 – сопло 3 – ...
... нефтепровода, м 25 ρ - средняя плотность, т/м3 0,870 P1 - давление насосной станции, кгс/см2 46 P2 - давление в конце участка, кгс/см2 1,5 δ - толщина стенки, мм 14 Таблица 2 - Данные для прочностного расчета Параметры Вариант 3 Dн - диаметр трубопровода наружный, мм 1220 Марка стали 12 Г2СБ t0 - температура при сварке замыкающего стыка, 0с ...
0 комментариев