Навигация
Построение переходного процесса
9 Построение переходного процесса
Построим переходный процесс для системы (6) с начальными условиями t=0, ω(0)= 1.1ω0, μ(0)=0, Z(0)=0 по формуле:
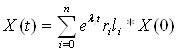 , где
, где
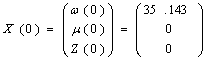 ,
, ![]() - правые и левые собственные вектора системы.
- правые и левые собственные вектора системы.
Собственные числа:
λ1= 1.59
λ2= – 2.79
λ3= –39.96
Матрица правых собственных векторов
![]()
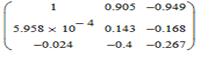
Матрица левых собственных векторов
![]()
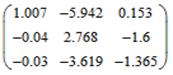
Получим переходный процесс
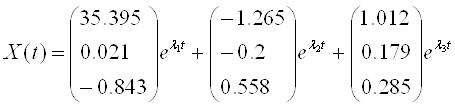
в котором
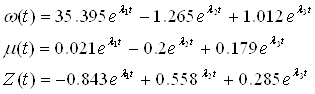
Построим графики ω(t), μ(t), Z(t)
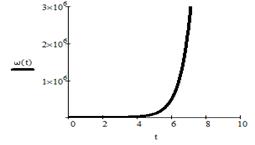
Рисунок 9 - Переходный процесс ω(t)
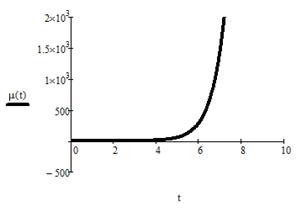
Рисунок 10 - Переходный процесс μ(t)
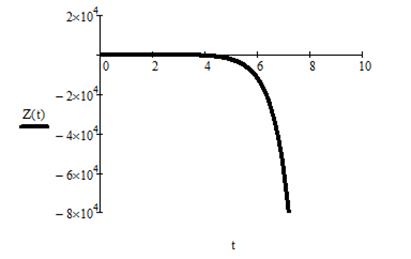
Рисунок 11 - Переходный процесс Z(t)
10 Нахождение передаточной функции для разомкнутой системы
Сделаем преобразование Лапласа над разомкнутой линейной системой, получим систему вида:
![]() , или
, или
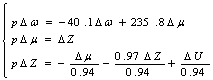
Выразим ∆μ из первого уравнения:
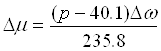
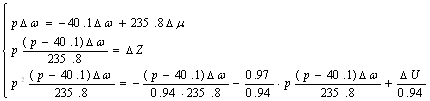
Выразим ∆ω через U:
![]() →
→
![]()
получили выражение вида ![]() , где W(p) есть передаточная функция комплексной переменной, имеющая вид:
, где W(p) есть передаточная функция комплексной переменной, имеющая вид:
![]() (8)
(8)
11 Амплитудная, фазовая, вещественная, мнимая и амплитудно-фазовая частотные характеристики
Подставим в передаточную функцию (8) в качестве комплексного аргумента iω, получим:
![]()
Умножим числитель и знаменатель правой части на число сопряженное знаменателю, получим и выделим действительную и мнимую части передаточной функции Re(ω) и Im(ω):
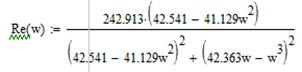
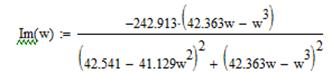
Построим графики.
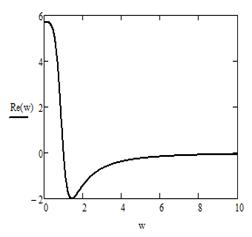
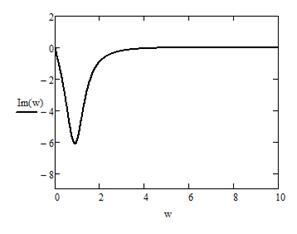
Рисунок 12 - График Re(ω) Рисунок 13 - График Im(ω)
Получим амплитудную, фазовую и амплитудно-фазовую частотные характеристики системы. Построим графики функций:
![]() - амплитудная характеристика (рис. 14).
- амплитудная характеристика (рис. 14).
![]() - фазовая характеристика (рис. 15).
- фазовая характеристика (рис. 15).
Для АФХЧ отложим на графике по вертикальной оси значения мнимой части, а по горизонтальной действительной части, при ω=1..100 с шагом 0.001. Рисунок 16.
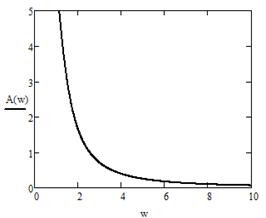
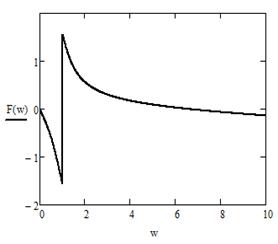
Рисунок 14 - График A(ω) Рисунок 15 - Графики Ф(ω)
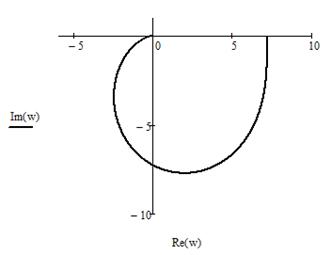
Рисунок 16 - Годограф АФЧХ
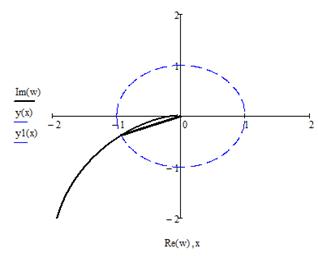
Рисунок 17 - Годограф АФЧХ
12 Оценка устойчивости системы по критерию Найквиста, по критерию Михайлова
Оценим устойчивость системы по критерию Найквиста. Годограф АФЧХ не охватывает точку (-1,0), следовательно, система устойчива. Найдем запасы устойчивости системы по фазе и по амплитуде.
Запас устойчивости по фазе – это угол, на который нужно повернуть годограф АФЧХ, чтобы он охватывал точку (-1,0).
Из уравнения ![]() получаем ω0=2.551. Вычислим значение действительной части при ω0, Re(ω0) = -0.926. Тогда запас устойчивости по фазе вычисляется как:
получаем ω0=2.551. Вычислим значение действительной части при ω0, Re(ω0) = -0.926. Тогда запас устойчивости по фазе вычисляется как:
![]()
Запас устойчивости по фазе равен 0.386 радиан.
Запас устойчивости системы по амплитуде – это расстояние от точки пересечения годографа АФЧХ с осью OX до точки (-1,0). Из уравнения ![]() получаем ω0=6.509. Вычислим Re(ω0)=-0.143. Тогда запас устойчивости системы по амплитуде будет равен 1-0.143=0,857
получаем ω0=6.509. Вычислим Re(ω0)=-0.143. Тогда запас устойчивости системы по амплитуде будет равен 1-0.143=0,857
Оценим устойчивость системы по критерию Михайлова. Подставим в характеристическое уравнение разомкнутой системы iω вместо λ, выделим действительную и мнимую часть. Построим годограф Михайлова, отложив на графике по вертикальной оси значения мнимой части, а по горизонтальной действительной части, при ω=1..100 с шагом 0.001 (рис. 18).
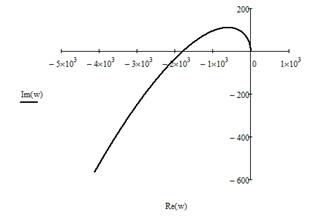
Рисунок 18 - Годограф Михайлова
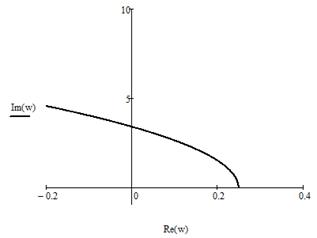
Рисунок 19 - Годограф Михайлова
Годограф Михайлова пересекает последовательно n квадрантов (n=3), следовательно, система устойчива.
Заключение
Результатом выполнения курсового проекта стало закрепление знаний по дисциплине «Основы теории управления», приобретены практические навыки для исследования поведения управляемой динамической системы, описанной системой дифференциальных уравнений. Были изучены возможности математических программных пакетов.
Библиографический список
1. Советов Б.Я. Яковлев С.А. Моделирование систем: Учеб. для вузов – 3-е изд. – М.: Высшая школа, 2001. – 343 с.
Похожие работы
... МПа, пределы измерений 0…1,6 МПа МС-П2 3 по месту Приборы в спецификации могут быть сгруппированы по позициям на схеме или по маркам. Часть 3. Современные системы управления производством. 1. Структура АСУ ТП. Характерной особенностью развития современной электронной промышленности является бурный рост, сопровождающийся столь же бурным снижением стоимости средств ...
... . В результате, на выходе реле сигнал будет непрерывным, но ступенчатым 3.2.2.3 Релейно-импульсные системы В них происходит квантование сигналов по времени и по уровню. К этому типу относятся цифровые системы управления, в частности АСУТП с используемым ВК. При большом количестве разрядов АЦП и ЦАП квантованием можно пренебречь, и отнести такие системы к импульсным. 3.2.2.4 Системы на ...
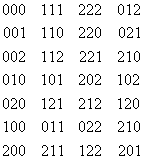
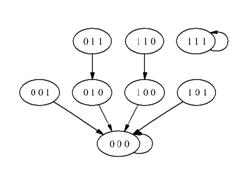
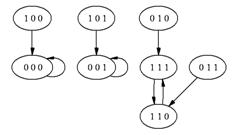
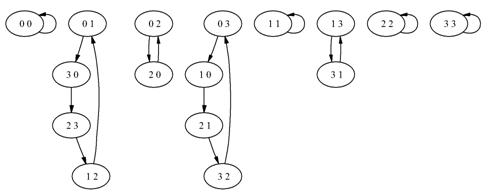
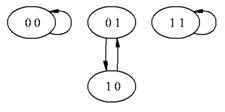
... 000 - , 001 - , 010 - , 011 - , 100 - , 101 - , 110 - , 111 - . Фазовое пространство изображено на рисунке 1.2.3. Рис. 1.2.3. Фазовое пространство . Теорема 1.2.1. Пусть – мономиальная динамическая система. Тогда – система конечных элементов тогда, и только тогда, когда и – системы конечных элементов. Доказательство. Из следствий 1.2.1 и 1.2.3, если – система конечных ...
... общественных отношений, т.е. к их динамике. На уровне общества индивидуальные действия отдельных индивидуумов или групп, а также их связи и отношения образуют системное качество. [9]Все вместе позволяет говорить о применимости к обществу как сложной динамической системе понятия самоорганизация, но. в то же время, отдельные личности или социальные группы, даже социальные слои общества в состоянии ...

0 комментариев