Навигация
Выбор метода реализации программы
3. Выбор метода реализации программы
Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений.
этот метод является одноступенчатым и одношаговым
требует информацию только об одной точке
имеет небольшую погрешность
значение функции рассчитывается при каждом шаге
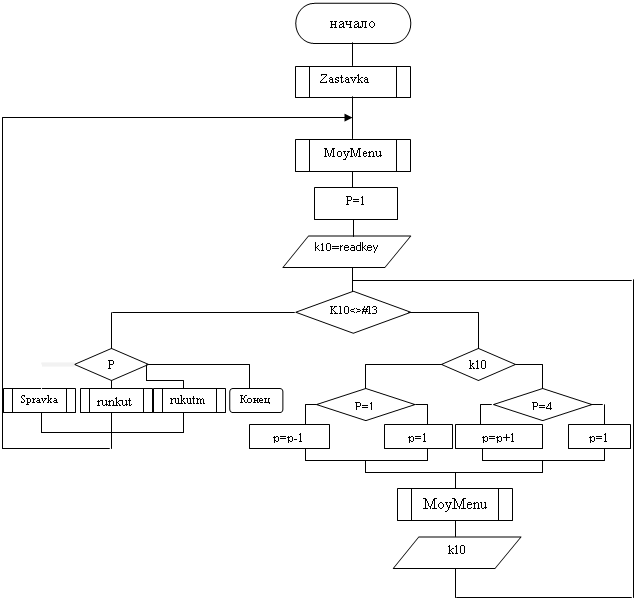
4. Блок-схема программмы
 |
![]() Процедура INIT
Процедура INIT
Вход
![]()
f1,C[1],C[2],C[3]
f1,k1,k2,k3,k4
f1,Xn,Xk,dp,n,eps,p
![]()
выход
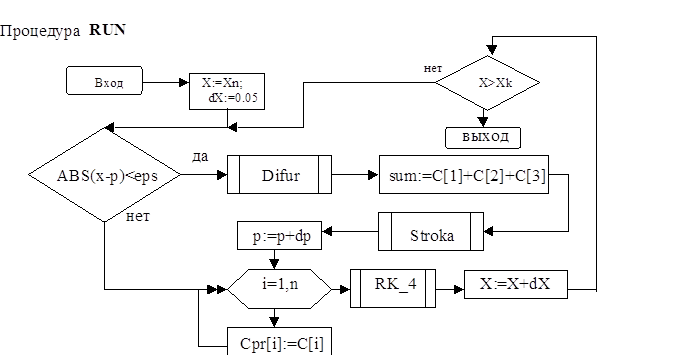
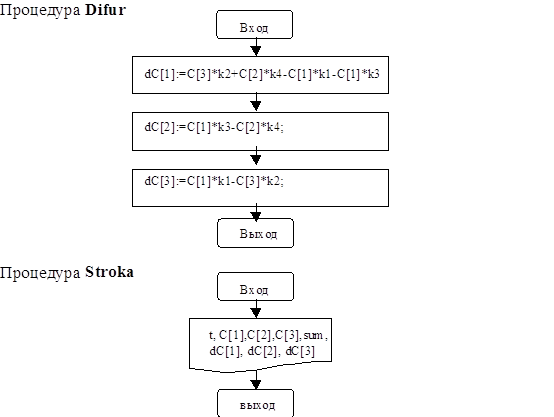
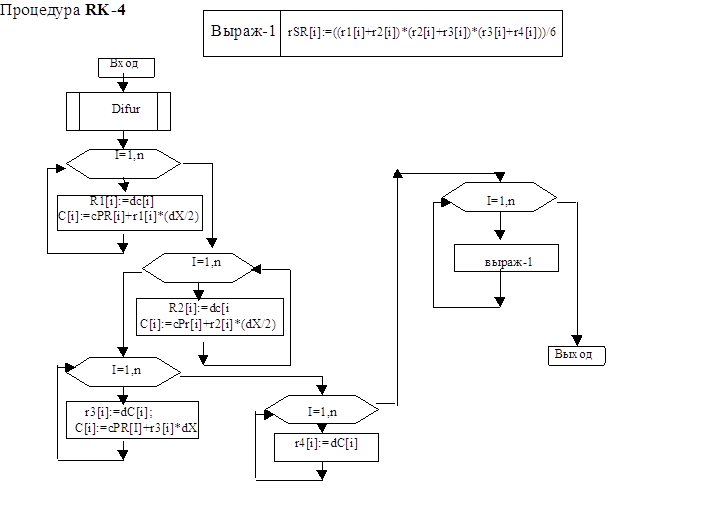
5. Программа
PROGRAM smith_04;USES crt; VAR i,n:integer; sum,k1,k2,k3,k4,p,dp,eps,Xn,Xk,X,dX:real; rSR,C,dC,r1,r2,r3,r4,cPR:array[1..3] of real;
f1,f2:text;
PROCEDURE Difur;
BEGIN
dC[1]:=C[3]*k2+C[2]*k4-C[1]*k1-C[1]*k3; {dcA}
dC[2]:=C[1]*k3-C[2]*k4; {dcB}
dC[3]:=C[1]*k1-C[3]*k2; {dcC}
END;
PROCEDURE RK_4;
BEGIN
Difur;
FOR i:=1 TO n DO BEGIN
r1[i]:=dC[i];
C[i]:=cPR[i]+r1[i]*(dX/2);
END;
Difur;
FOR i:=1 TO n DO BEGIN
r2[i]:=dC[i];
C[i]:=cPr[i]+r2[i]*(dX/2);
END;
Difur;
FOR i:=1 TO n DO BEGIN
r3[i]:=dC[i];
C[i]:=cPR[I]+r3[i]*dX;
END;
Difur;
FOR i:=1 TO n DO r4[i]:=dC[i];
FOR i:=1 TO n DO rSR[i]:=((r1[i]+r2[i])*(r2[i]+r3[i])*(r3[i]+r4[i]))/6;
END;
PROCEDURE STROKA;
BEGIN
WRITE(f2,'|',x:4:1,'|',c[1]:7:3,'|',c[2]:7:3,'|',c[3]:7:3,'|');
WRITE(f2,sum:3:0,'|',dc[1]:7:3,'|',dc[2]:7:3,'|',dc[3]:7:3,'|');
WRITELN(f2);
END;
PROCEDURE RUN;
BEGIN
WRITE('Step 3: Calculating data and writting results to file : out.rez');
X:=Xn;
dX:=0.05;
REPEAT
IF (ABS(x-p)<eps) THEN BEGIN
Difur;
sum:=C[1]+C[2]+C[3];
STROKA;
p:=p+dp; END;
FOR i:=1 TO n DO Cpr[i]:=C[i];
RK_4;
X:=X+dX;
UNTIL(X>Xk);
WRITELN(' - done.');
END;
PROCEDURE INIT;
BEGIN
ClrScr;
WRITELN('Smith-04: v1.0 (c) 1998 by Mike Smith smith01@home.bar.ru ');
WRITELN;
WRITELN;
WRITE('Step 1: Read data from file : in.dat');
ASSIGN(f1,'in.dat');
RESET(f1);
READLN(f1,C[1],C[2],C[3]);
READLN(f1,k1,k2,k3,k4);
READLN(f1,Xn,Xk,dp,n,eps,p);
WRITELN(' - done.');
ASSIGN(f2,'out.rez');
REWRITE(f2);
WRITE('Step 2: Write header to file : out.rez');
WRITELN(f2,'');
WRITELN(f2,'| t,c| Ca,% | Cb,%| Cc,% | SUM | dCa | dCb | dCc |');
WRITELN(f2,'=');
WRITELN(' - done.');
END;
PROCEDURE DONE;
BEGIN
WRITELN('Step 4: Close all files and exiting...');
CLOSE(f1);
WRITELN(f2,'=');
CLOSE(f2);
WRITELN;
END;
BEGIN
INIT;
RUN;
DONE;
END.
6. Идентификация переменных
Таблица 1
7. Результаты расчета
Таблица 2
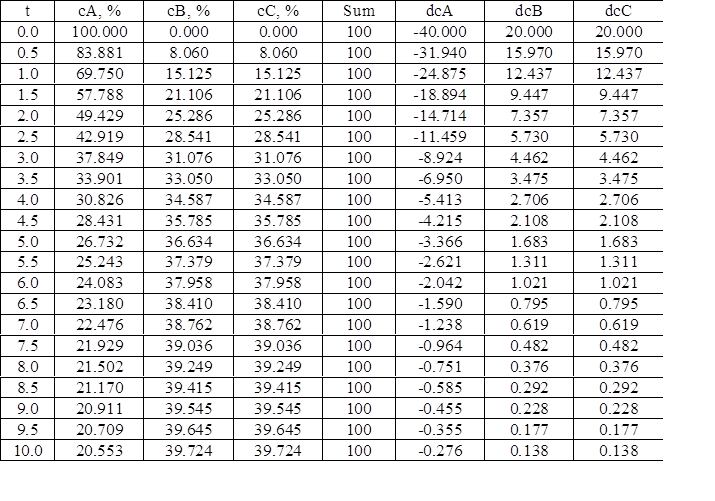
8. Обсуждение результатов расчета.
В результате расчета кинетической схемы процесса на языке Паскаль методом Рунге-Кутты, были получены результаты зависимости изменения концентрации реагирующих веществ во времени. Исходя из полученных результатов, можно сделать вывод, что расчет произведен верно, так как, исходя из полученных значений скоростей реакций можно сделать вывод, что соблюдается баланс скоростей химической реакции.
Рассмотрим процесс подробнее. Вещество А на протяжении всего процесса расходуется на образование веществ В и С. Концентрации вещества А в начальный момент времени расходуется быстрее, чем концентрации его же в конце процесса. Это обусловлено тем, что скорость химической реакции зависит от концентрации реагирующего вещества. Производная имеет знак «минус». Это говорит о том, что вещество расходуется. Следовательно, чем выше концентрация вещества, вступающего в процесс, тем выше скорость его реагирования с другими веществами. Вещества В и С образуются пропорционально, так как, исходя из кинетической схемы процесса и значений констант скоростей химической реакции, видно, что образование этих веществ и расходование этих веществ, одинаково. Производная имеет знак «плюс». Это говорит о том, что вещество образуется.
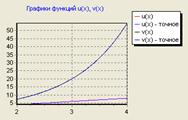
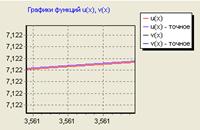
График. 4
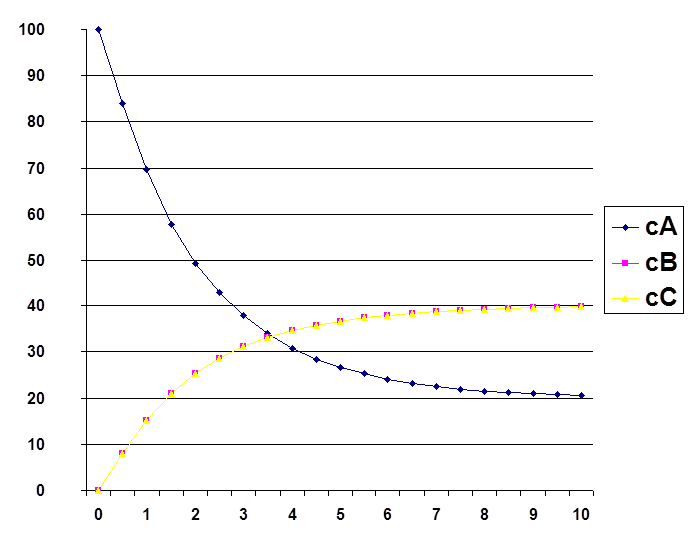
Это видно также и по результатам расчета, на протяжении всего времени исследования процесса концентрации и скорости веществ В и С одинаковы. В этом можно убедиться по виду графической зависимости концентрации веществ В и С от времени.
Можно сказать, что процесс протекает в сторону увеличения концентрации веществ В и С и уменьшения концентрации вещества А. Процесс будет протекать до момента установления равновесия, но в данном случае равновесие не установлено, так как вещества продолжают расходоваться и образовываться. На протяжении всего процесса ни одно из образующихся веществ не поменяло знак производной. Это говорит о том, что процесс протекает в одну сторону.
Похожие работы
... при использовании этого метода функцию необходимо вычислять четыре раза3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений этот метод является одноступенчатым и одношаговым ...
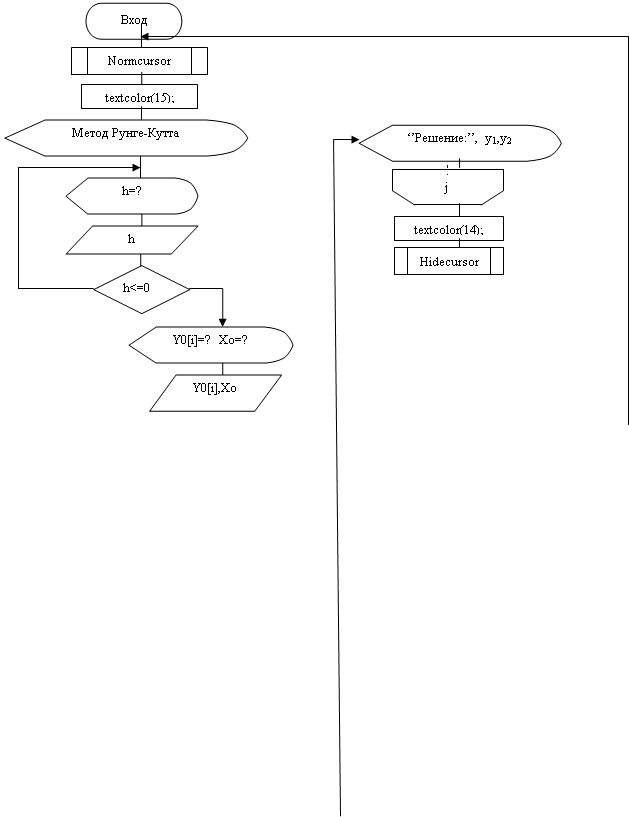
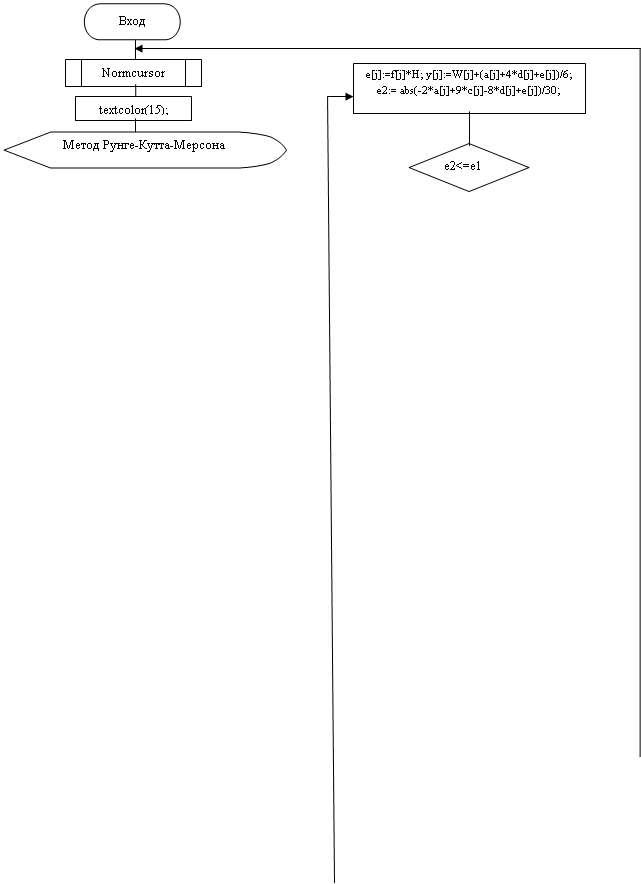
... уравнений методом Рунге-Кутта при выборе пункта меню «Метод Рунге-Кутта» с использованием включения курсора, а также строки-подсказки о возврате в меню. Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта-Мерсона при выборе пункта меню «Метод Рунге-Кутта-Мерсона» с использованием включения курсора, а также строки-подсказки о возврате в меню. ...
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
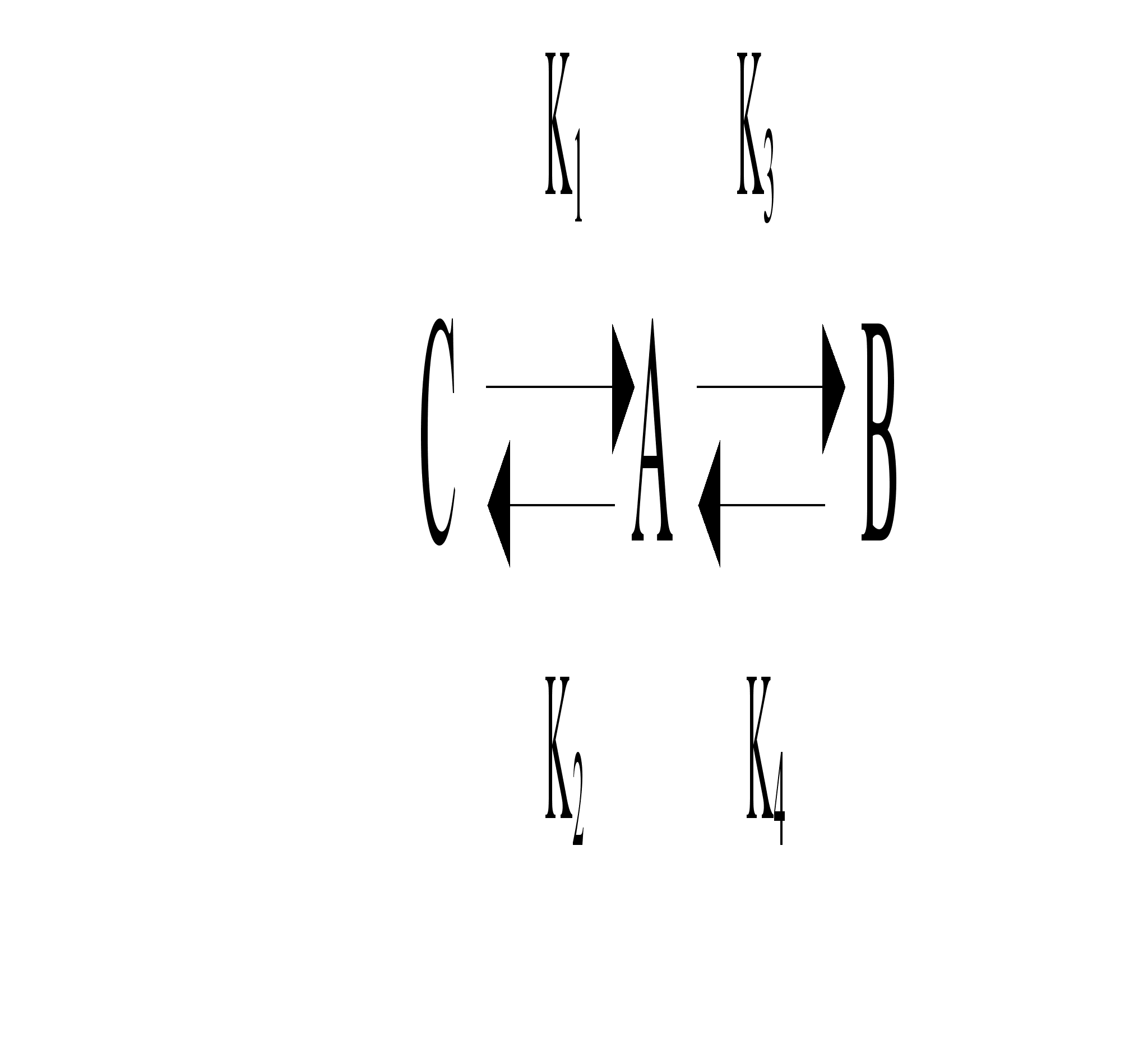
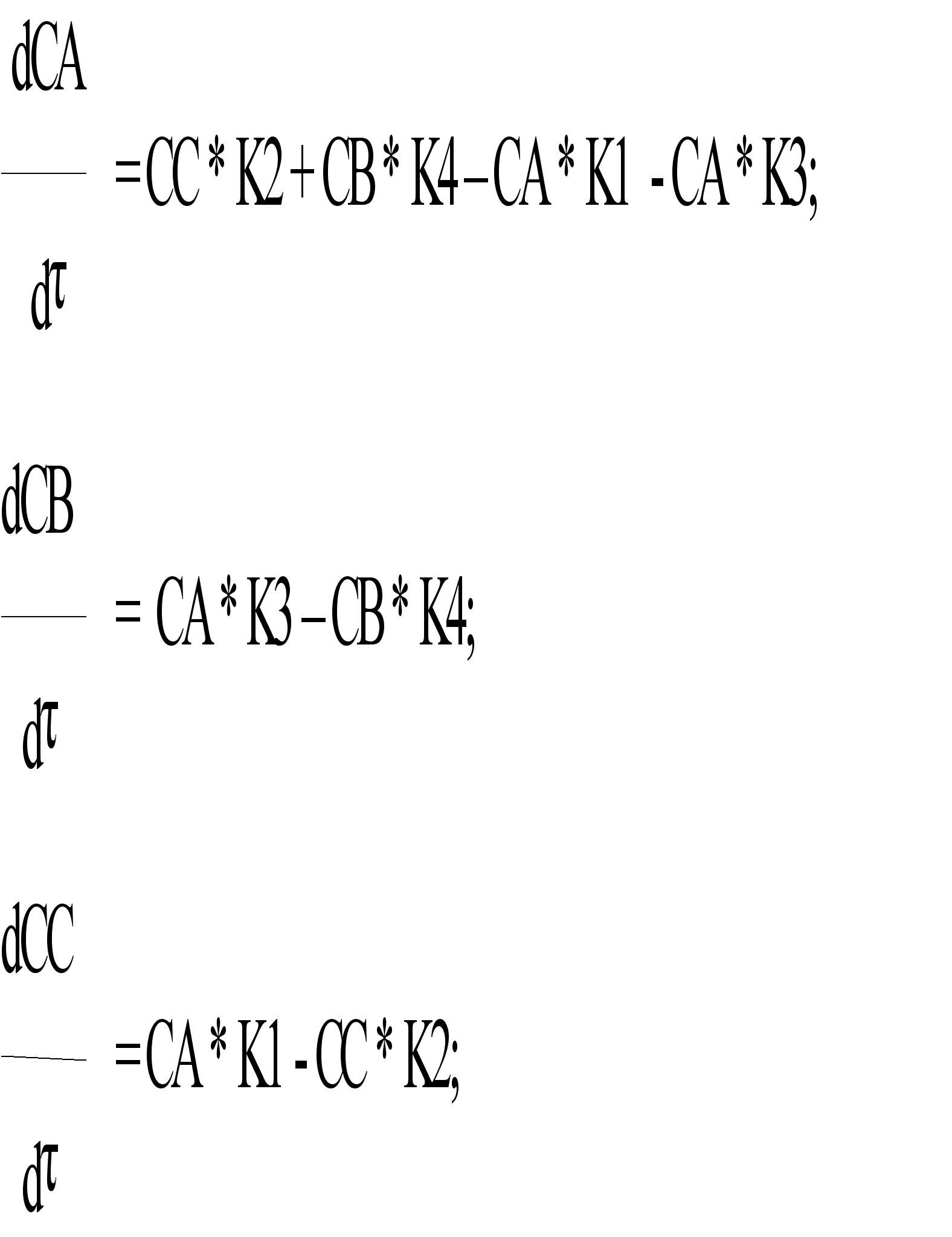
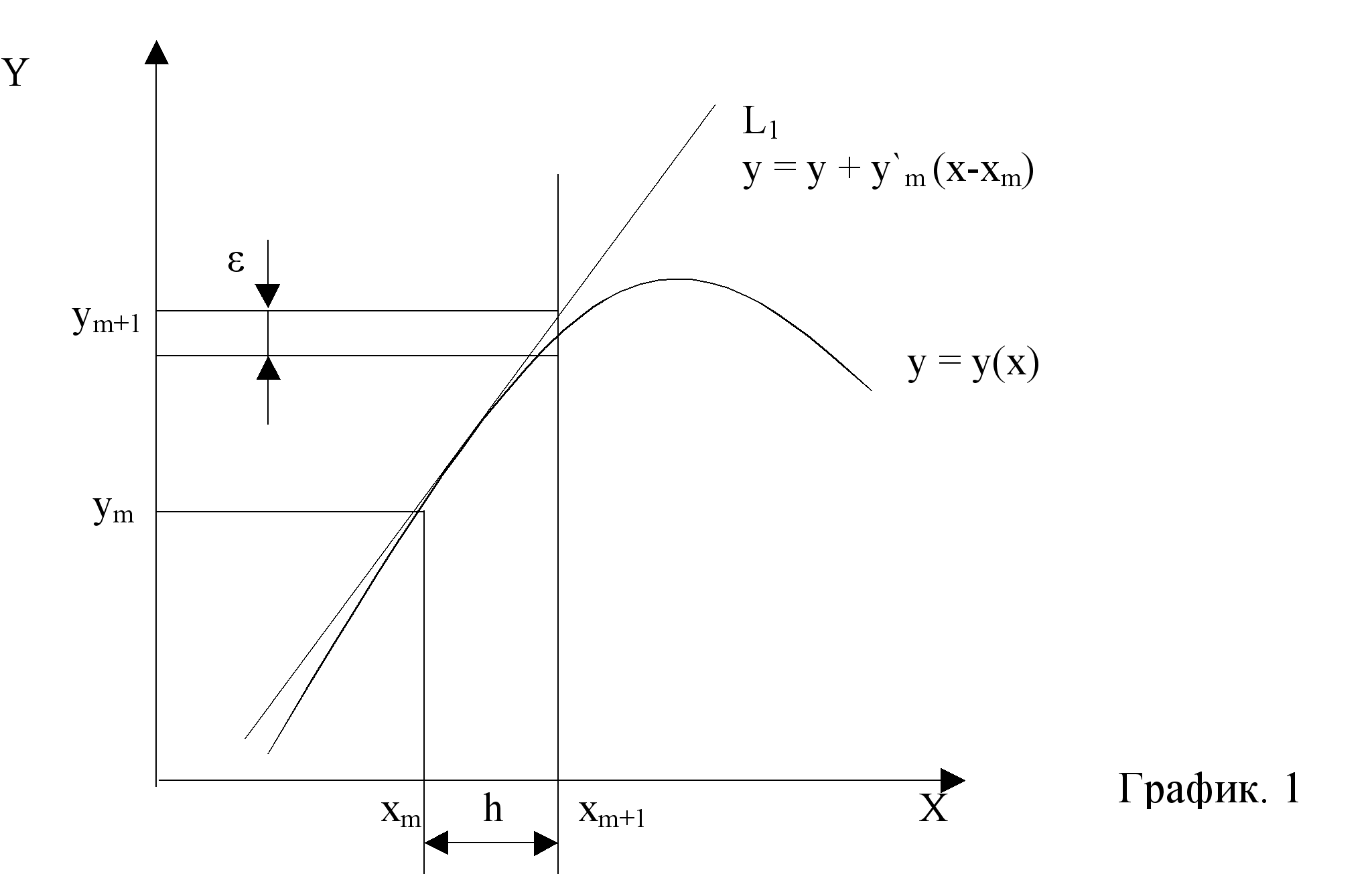

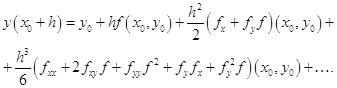
0 комментариев