Навигация
9. Инструкция к программме
Итак, программа состоит из 3 основных процедур:
Init - процедура инициалиации, включающую в себя ввод данных;
Run - процедура вычисления и обработки результатов, включает в себя вызов двух вспомогательных процедур Difur, RK-4, Stroka, первая из которых отвечает за вычисление, а последняя - за вывод результатов в файл в табличном виде;
Done - процедура подготовки к выходу из программы;
и трех вспомогательных:
Difur - процедура вычисления производных (изменение концентрации веществ за единикцу времени )
RK-4 - используя значения производных, вычисленных процедурой Difur, вычисляет последущие концентрации веществ методом Рунге-Кутта
Stroka - процедура вывода результата в файл в табличном виде
Рассмотрим все эти процедуры поподробнее:
Процедура INIT:
![Подпись: PROCEDURE INIT; BEGIN ClrScr; WRITE('Step 1: Read data from file : in.dat'); ASSIGN(f1,'in.dat'); RESET(f1); READLN(f1,C[1],C[2],C[3]); READLN(f1,k1,k2,k3,k4); READLN(f1,Xn,Xk,dp,n,eps,p); WRITELN(' - done.'); ASSIGN(f2,'out.rez'); REWRITE(f2); WRITE('Step 2: Write header to file : out.rez'); WRITELN(f2,’_____________________________________'); WRITELN(f2,'¦t,c ¦ Ca,% ¦ Cb,% ¦ Cc,% ¦SUM¦ dCa ¦ dCb ¦ dCc ¦'); WRITELN(f2,'_____________________________________'); WRITELN(' - done.'); END; ](/images/referats/a6/18221/21.png)
В данной процедуре задействованы операторы ввода/вывода Wite/Read, оператор модуля Crt - CrlScr - очистка экрана, файлового ввода/вывода - Reset/Rewrite – открытие файла для чтения и создание нового файла, соответственно. Данная процедура выполняет функцию инициализации программных данных, считывание данных из файла in.dat, создание, открытие на запись файла out.rez и запись в него шапки таблицы результатов.
Процедура RUN:
![Подпись: PROCEDURE RUN; BEGIN X:=Xn; dX:=0.05; REPEAT IF (ABS(x-p)<eps) THEN BEGIN Difur; sum:=C[1]+C[2]+C[3]; STROKA; p:=p+dp; END; FOR i:=1 TO n DO Cpr[i]:=C[i]; RK_4; X:=X+dX; UNTIL(X>Xk); WRITELN(' - done.'); END; ](/images/referats/a6/18221/22.png)
В данной процедуре задействованы операторы цикла Repeat/Until, и For/Do c операторами условного перехода IF/Then. В зависимости от условий вызываются процедуры Difur и Strok. В теле цикла постоянно вызывается процедура RK-4 вызывающая 4 раза функцию Difur.
Процедура DONE:

В данной процедуре задействованы оператор работы с файлами Close, который закрывает файлы с исходными данными и файл с полученными в резуультате вычислений результатами.
Процедура DIFUR:
![Подпись: PROCEDURE Difur; BEGIN dC[1]:=C[3]*k2+C[2]*k4-C[1]*k1-C[1]*k3; dC[2]:=C[1]*k3-C[2]*k4; dC[3]:=C[1]*k1-C[3]*k2; END; ](/images/referats/a6/18221/24.png)
Данная процедура вычисляет производную изменения концентрации везества за единицу времени.
Процедура STROKA:
![Подпись: PROCEDURE STROKA; BEGIN WRITE(f2,'¦',x:4:1,'¦',c[1]:7:3,'¦',c[2]:7:3,'¦',c[3]:7:3,'¦'); WRITE(f2,sum:3:0,'¦',dc[1]:7:3,'¦',dc[2]:7:3,'¦',dc[3]:7:3,'¦'); WRITELN(f2); END; ](/images/referats/a6/18221/25.png)
Данная процедура с помощью оператора вывода WRITE записывает результаты в файл, соответствующий файловой переменной F2, назначенной коммандой ASSIGN в процедуре INIT
![Подпись: PROCEDURE RK_4; BEGIN Difur; FOR i:=1 TO n DO BEGIN r1[i]:=dC[i]; C[i]:=cPR[i]+r1[i]*(dX/2); END; Difur; FOR i:=1 TO n DO BEGIN r2[i]:=dC[i]; C[i]:=cPr[i]+r2[i]*(dX/2); END; Difur; FOR i:=1 TO n DO BEGIN r3[i]:=dC[i]; C[i]:=cPR[I]+r3[i]*dX; END; Difur; FOR i:=1 TO n DO r4[i]:=dC[i]; FOR i:=1 TO n DO rSR[i]:=((r1[i]+r2[i])*(r2[i]+r3[i])*(r3[i]+r4[i]))/6; END; ](/images/referats/a6/18221/26.png)
Процедура RK-4:
Данная процедура, используя вызовы процедур Difur, а также циклы операторы цикла FOR, вычисляет последуущие концентрации веществ по предидущим точкам.
Программа представляет собой 2 файла – файл с исходным текстом на языке Паскаль smith.pas и исполняемый модуль smith.exe скомпилированный компилятором TNT Pascal 3.25 фирмы Layer`s Ins.
Исполняемый модуль программы предназначен для запуска в операционных системах: MS Dos, Windows95, Windows NT, OS/2, а также в X-windows под Linux (при наличии эмулятора )
Для нормальной работы программе необходимо 640 кb «нижней» памяти и 20 kb дискового пространства. Согласитесь – требования минимальные, учитывая то, что сама программа абсолютно не требовательна к процессору.
В процессе работы программа считывает данные из файла in.dat и записывает результаты работы в файл out.rez в табличном виде. Исходный файл программма открывает стандартными средствами ОС, не проверяя его наличие перед работой, поэтому, если данный файл не будет доступен в каталоге, в котором расположена программа, компилятор выдаст сообщение об ошибке. Если Вы после запуска программы увидели что-то типа «Runtime error 202 at 0000:0A86» - это всего лишь значит, что программа не смогла найти файл с исходными данными в текущем каталоге. Если Вы забыли поместить его туда, скопируйте этот файл в каталог с программой и запустите исполняемый модуль еще раз. Если данный файл у Вас отсутствует, Вам прийдется сделать его самому.
Для этого в любом текстовом редакторе наберите 3 выделенных строчки и сохраните созданный файл с именем in.dat
100 0 0
0.2 0.1 0.2 0.1
0 10 0.5 3 0.05 0
Создав файл и скопировав его к исполняемому модулю программы, запустите исполняемый модуль еще раз.
В процессе работы программа будет выдавать сообщения об успешном окончании каждого блока. Если все прошло нормально, то на экране своего компьютера Вы увидите следуще сообщения:

Step 1: Read data from file : in.dat - done.
Step 2: Write header to file : out.rez - done.
Step 3: Calculating data and writting results to file : out.rez - done.
Step 4: Close all files and exiting...
Первый шаг (step1) сообщает, что данные из файла in.dat были успешно прочитаны
Второй – о том что программа успешно создала выходной файл out.rez и записала в него шапку таблицы с данными
В третьем сообщении сказано, что данные успешно посчитаны и записаны в выходной файл out.rez
Четвертое сообщение сообщает об окончании вычислений и завершении программы.
После того, как программа отработает, Вы сможете познакомится с результатами, которые были вычислены и помещены в файл результатов out.rez. Просмотрев его любой программой просмотра текстовых файлов или вывев его на печать, вы получите таблицу c результатами.
10. Заключение.
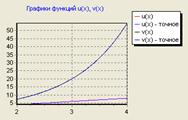
В результате выполнения расчета получена зависимость изменения концентрации вещества во времени. Из расчета следует, что на протяжении всего процесса вещество А расходовалось на образование В и С. Процесс не достиг конечного состояния (не достиг равновесия) Максимум концентрации вещества наблюдался при следующих значениях времени:
при начальном значении времени max соответствовал веществу А;
при значении времени, равном 10 часам, max соответствовал веществам B и С,
однако, это не является максимумом концентрации веществ в процессе
вообще, так как вещества B и С продолжают образовываться;
В ходе выполнения работы был произведен расчет системы дифференциальных уравнений методом Рунге-Кутты четвертого порядка, произведен расчет кинетической схемы процесса при изотермических условиях при данных значениях концентраций и констант скоростей. Расчет произведен с малой величиной погрешности.
Список литературы
1. Мудров А.Е.Численные методы для ПЭВМ на языках Паскаль, Фортран и Бейсик. МП “Раско”, Томск, 1991 г.
Для подготовки данной работы были использованы материалы с сайта http://www.ed.vseved.ru/
Похожие работы
... при использовании этого метода функцию необходимо вычислять четыре раза3. Выбор метода реализации программы Исходя из вышеизложенного, для решения систем дифференциальных уравнений мы выбираем наиболее точный метод решения – метод Рунге-Кутта 4 порядка, один из самых употребляемых методов интегрирования дифференциальных уравнений этот метод является одноступенчатым и одношаговым ...
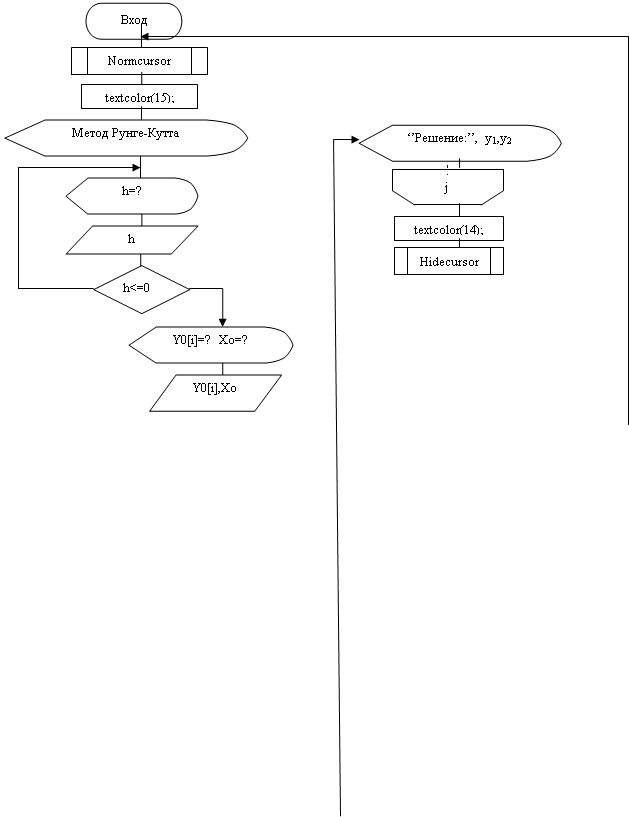
... уравнений методом Рунге-Кутта при выборе пункта меню «Метод Рунге-Кутта» с использованием включения курсора, а также строки-подсказки о возврате в меню. Запустить подпрограмму-процедуру поиска решения системы дифференциальных уравнений методом Рунге-Кутта-Мерсона при выборе пункта меню «Метод Рунге-Кутта-Мерсона» с использованием включения курсора, а также строки-подсказки о возврате в меню. ...
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
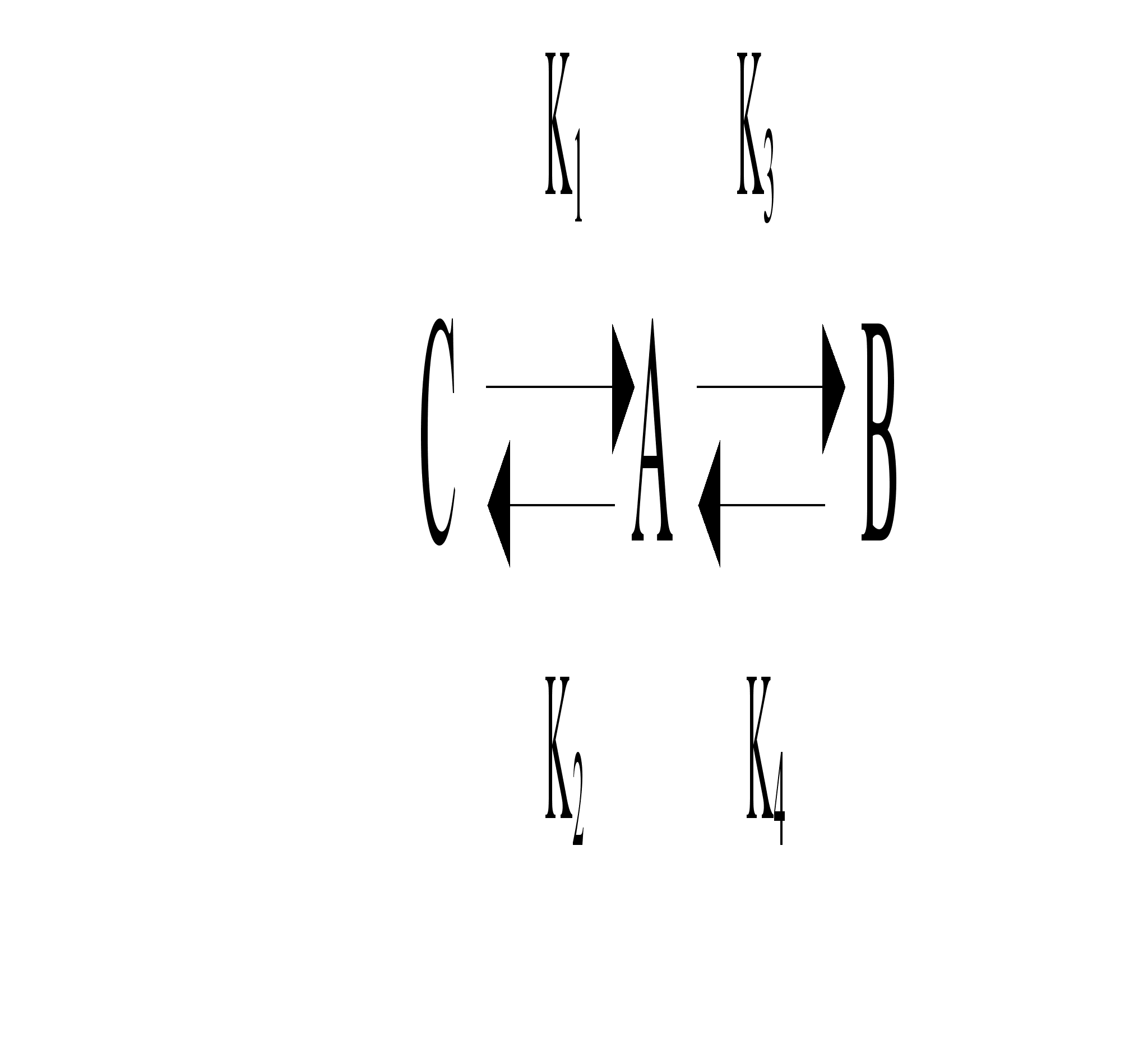

0 комментариев