Навигация
Найдите стандартную ошибку регрессии
7. Найдите стандартную ошибку регрессии.
Решение
1. Оценку значимости уравнения регрессии в целом дает F-критерия Фишера:
Fфакт = ![]()
где m- число факторных признаков в уравнении регрессии; R – линейный коэффициент множественной корреляции.
В нашем примере F-критерий Фишера составляет
Fфакт = ![]() = 249,864
= 249,864
Fтабл = 3,42; α = 0,05.
Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу Н0, так как Fтабл = 3,42 < Fфакт = 249,864. С вероятностью 0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи R2.
2. Скорректированный коэффициент множественной корреляции находится как корень из скорректированного коэффициента множественной детерминации (R2скорр):
R скор = ![]() =
=![]() =
= ![]() = 0,976
= 0,976
3. Линейное уравнение множественной регрессии y от x1 и x2 имеет вид:
4. y = a + b1*x1 + b2*x2.
5. По условию оно нам дано:
![]() = - 2,229 + 0,039* x1 + 0,303* x2
= - 2,229 + 0,039* x1 + 0,303* x2
Построим искомое уравнение в стандартизованном масштабе:
ty = β1*tx1 + β2*tx2.
Расчет β-коэффициентов выполним по формулам:
β1 = ![]() =
= ![]() = 0,345;
= 0,345;
β2 = ![]() =
= ![]() = 0,761.
= 0,761.
Получим уравнение
ty = 0,345*tx1 + 0,761*tx2.
6. Для характеристики относительной силы влияния x1 и x2 на y рассчитаем средние коэффициенты эластичности:
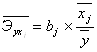 ;
;
![]() = 0,552%;
= 0,552%; ![]() = 0,532%.
= 0,532%.
С увеличением валового производства молока x1 на 1% от его среднего уровня валовая продукция сельского хозяйства y возрастает на 0,55% от своего среднего уровня; при повышении валового производства мяса x2 на 1% валовая продукция сельского хозяйства y возрастает на 0,53% от своего среднего уровня. Очевидно, что сила влияния валового производства молока x1 на валовую продукцию сельского хозяйства y оказалась большей, чем сила влияния валового производства мяса x2, но правда не намного.
Частные коэффициенты корреляции рассчитываются по формуле:
 =
= ![]() = 0,817,
= 0,817,
т.е. при закреплении фактора x2 на постоянном уровне корреляция y и x1 оказывается более высокой (0,817 против 0,717);
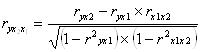 =
= ![]() = 0,953,
= 0,953,
т. е. при закреплении фактора x1 на постоянном уровне влияние фактора x2 на y оказывается более высокой (0,953 против 0,930);
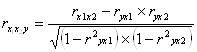 =
= ![]() = - 0,692
= - 0,692
7. Результаты дисперсионного анализа представлены в табл. 2.1.
Таблица 2.1
| Вариация результата, y | Число степеней свободы | Сумма квадратов отклонений, S | Дисперсия на одну степень свободы, s2 | Fфакт | Fтабл α =0,05, k1 = 2, k2 = 23 |
| Общая | Df = n-1 = 25 | 35113 | - | - | - |
| Факторная - за счет x1 - за счет дополнительногоx2 | k1 = m = 2 1 1 | 33568,028 18051,207 15516,821 | 16784,014 18051,207 15516,821 | 249,864 268,728 230,999 | 3,42 4,28 4,28 |
| Остаточная | k2 = n-m-1 = 23 | 1544,972 | 67,173 | - | - |
Sобщ = ![]() = 1350,5 * 26 = 35113;
= 1350,5 * 26 = 35113;
Sфакт = ![]() = 1350,5 * 26 * 0,956 = 33568,028;
= 1350,5 * 26 * 0,956 = 33568,028;
Sфакт x1 =![]() = 1350,5 * 26 * 0,7172 = 18051,207;
= 1350,5 * 26 * 0,7172 = 18051,207;
Sфакт x2 = Sфакт - Sфакт x1 = 33568,028 – 18051,207 = 15516,821;
Sост = ![]() = Sобщ - Sфакт = 35113 – 33568,028 = 1544,972;
= Sобщ - Sфакт = 35113 – 33568,028 = 1544,972;
Fфакт = ![]() =
= ![]() = 249,864;
= 249,864;
Fфактx1 = ![]() =
= ![]() = 268,728;
= 268,728;
Fчастнx2 = ![]() =
= ![]() = 230,999.
= 230,999.
![]() = 16784,014;
= 16784,014;
![]() = 15516,821;
= 15516,821;
![]() = 18051,207
= 18051,207
Включение в модель фактора x2 после фактора x1 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т. е. следствием дополнительного включения в модель систематически действующего фактора x2, так как Fчастнx2 = 230,999 > Fтабл = 4,28.
8. Оценка с помощью t-критерия Стьюдента значимости коэффициента b2 связана с сопоставлением его значения с величиной его случайной ошибки: mb2.
Расчет значения t-критерия Стьюдента для коэффициента регрессии линейного уравнения находится по следующей формуле:
![]() = 15,199.
= 15,199.
При α = 0,05; df = n-m-1 = 26-2-1 = 23; tтабл = 2,07. Сравнивая tтабл и tфакт, приходим к выводу, что так как ![]() = 15,199 > 2,07 = tтабл, коэффициент регрессии b2 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе.
= 15,199 > 2,07 = tтабл, коэффициент регрессии b2 является статистически значимым, надежным, на него можно опираться в анализе и в прогнозе.
9. Стандартная ошибка регрессии рассчитывается по следующей формуле:
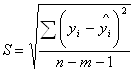 =
= ![]() = 8,196.
= 8,196.
Задача 3
Рассматривается модель вида

где
Сt – расходы на потребление в текущий период,
Сt-1 – расходы на потребление в предыдущий период,
Rt – доход текущего периода,
Rt-1 – доход предыдущего периода,
Yt – инвестиции текущего периода.
Ей соответствует следующая приведенная форма (построена по районам области)
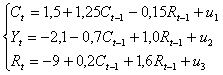
Задание
1. Проведите идентификацию модели.
2. Укажите способы оценки параметров каждого уравнения структурной модели.
3. Найдите структурные коэффициенты каждого уравнения, если известны следующие данные:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Yt | 4 | 4 | 6 | 10 | 9 | 8 | 7 | 6 | 8 | 12 | 8 | 16 |
| Сt | 14 | 13 | 15 | 20 | 20 | 14 | 16 | 12 | 12 | 21 | 12 | 17 |
| Rt-1 | 15 | 14 | 16 | 22 | 26 | 18 | 18 | 15 | 19 | 28 | 18 | 26 |
| Сt-1 | 12 | 11 | 12 | 15 | 17 | 12 | 14 | 10 | 11 | 20 | 12 | 16 |
Решение
1. Модель имеет три эндогенные Н (Сt, Yt, Rt). Причем переменная Rt задана тождеством. Поэтому практически статистическое решение необходимо только для первых двух уравнений системы, которые необходимо проверить на идентификацию. Модель содержит две предопределенные D (Сt-1, Rt-1) переменные.
Проверим каждое уравнение системы на необходимое и достаточное условия идентификации.
Проверим необходимое условие идентификации для уравнений модели.
I уравнение.
Н: эндогенных переменных – 2 (Сt, Rt), отсутствующих предопределенных переменных – 1 (Rt-1).
Следовательно, по счетному правилу D + 1 = H (1 + 1 = 2) уравнение идентифицируемо.
II уравнение.
Н: эндогенных переменных – 1 (Yt); переменная Rt в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с переменной Rt-1.
отсутствующих предопределенных переменных – 1 (Сt-1).
Следовательно, по счетному правилу D + 1 > H (1 + 1 > 1) уравнение сверхидентифицировано.
III уравнение.
Третье уравнение представляет собой тождество, параметры которого известны. Необходимости в его идентификации нет.
Следовательно, рассматриваемая в целом структурная модель сверхидентифицируема по счетному правилу.
Проверим для каждого из уравнений достаточное условие идентификации.
Для этого составим матрицу коэффициентов при переменных модели:
| Сt | Yt | Rt | Rt-1 | Сt-1 | |
| I уравнение | -1 | 0 | b11 | 0 | b12 |
| II уравнение | 0 | -1 | b21 | -b21 | 0 |
| III уравнение | 1 | 1 | -1 | 0 | 0 |
В соответствии с достаточным условием идентификации определитель матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть равен числу эндогенных переменных модели минус 1, т. е. 3-1=2.
I уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
| Уравнение | Отсутствующие переменные | |
| Yt | Rt-1 | |
| Второе | -1 | -b21 |
| Третье | 1 | 0 |
Определитель матрицы не равен 0 (Det A = -1*0 – (1*-b21) ![]() 0), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.
0), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.
II уравнение.
Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид:
| Уравнение | Отсутствующие переменные | |
| Сt | Сt-1 | |
| Первое | -1 | b12 |
| Третье | 1 | 0 |
Определитель матрицы не равен 0 (Det A = -1*0 – (1*b12) ![]() 0.), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.
0.), ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации.
Похожие работы
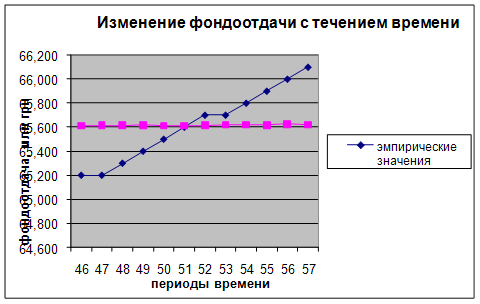
... активной части основных фондов в этом же периоде на 24,862 – 23,3 = 1,562 млн.грн по сравнению с двенадцатым периодом. Выводы и рекомендации Проведенный анализ технико-экономических показателей работы предприятия позволяет сделать вывод о том, что оно работает стабильно и постепенно развивается, хотя и невысокими темпами. Дальнейший рост фондоотдачи предприятия может быть обеспечен неск
... удобрений на 1 кг. Средняя ошибка аппроксимации = 1/25 ∙494,486 = 19,780% Ошибка аппроксимации 19,78 % > 12% – модель ненадежна и статистически незначима. Оценим тесноту связи с помощью показателей корреляции и детерминации. Тесноту связи показывает коэффициент корреляции: δx- показывает, что в среднем фактор Х меняется в пределах , 3,46 ± 4,672 δу - ...
... Hо. №29. ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. ИНТЕРПРИТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. Величину L, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один ил более моментов времени, — лаговыми переменными. Эконометрическое моделирование осуществляется с ...
... , характеризующих результаты экономической деятельности, структуру экономики и важнейшие взаимосвязи в национальном хозяйстве. Основным положением системы национальных счетов является расчет обобщающих показателей развития различных отраслей в рамках национальной экономики на различных стадиях воспроизводственных процессов, а также взаимоувязка этих показателей как между собой, так и во временных ...


0 комментариев