Навигация
Первое уравнение идентифицируемое, следовательно, для его решения применяется косвенный метод наименьших квадратов
2. Первое уравнение идентифицируемое, следовательно, для его решения применяется косвенный метод наименьших квадратов.
Косвенный метод наименьших квадратов (МНК):
- Составить приведенную форму модели и определить численные значения параметров каждого уравнения системы обычным МНК.
- Путем алгебраических преобразований переходим от приведенной формы к уравнениям структурной формы модели и получаем численные оценки структурных параметров.
Для решения второго уравнения, а оно у нас сверхидентифицируемое, применяется – двухшаговый метод наименьших квадратов.
Двушшаговый метод:
- Составить приведенную форму модели и определить численные значения параметров каждого уравнения системы обычным МНК.
- Выявляем эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находим расчетные значения по соответствующим уравнениям приведенной формы модели.
- Обычным МНК определяем параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
3. Найдем структурные коэффициенты первого и второго уравнений на основании исходных данных.
Составим расчетную таблицу (Rt = Ct + Yt ; обозначим d Rt = Rt - Rt-1).
Таблица 3.1 Расчетная таблица
| № | Yt | Ct | Rt-1 | Ct-1 | Rt | dRt | Yt*dRt | (dRt)2 | (Rt)2 | (Ct-1*Rt | Ct*Rt | (Ct-1)2 | Ct*Ct-1 |
| 1 | 4 | 14 | 15 | 12 | 18 | 3 | 12 | 9 | 324 | 216 | 252 | 144 | 168 |
| 2 | 4 | 13 | 14 | 11 | 17 | 3 | 12 | 9 | 289 | 187 | 221 | 121 | 143 |
| 3 | 6 | 15 | 16 | 12 | 21 | 5 | 30 | 25 | 441 | 252 | 315 | 144 | 180 |
| 4 | 10 | 20 | 22 | 15 | 30 | 8 | 80 | 64 | 900 | 450 | 600 | 225 | 300 |
| 5 | 9 | 20 | 26 | 17 | 29 | 3 | 27 | 9 | 841 | 493 | 580 | 289 | 340 |
| 6 | 8 | 14 | 18 | 12 | 22 | 4 | 32 | 16 | 484 | 264 | 308 | 144 | 168 |
| 7 | 7 | 16 | 18 | 14 | 23 | 5 | 35 | 25 | 529 | 322 | 368 | 196 | 224 |
| 8 | 6 | 12 | 15 | 10 | 18 | 3 | 18 | 9 | 324 | 180 | 216 | 100 | 120 |
| 9 | 8 | 12 | 19 | 11 | 20 | 1 | 8 | 1 | 400 | 220 | 240 | 121 | 132 |
| 10 | 12 | 21 | 28 | 20 | 33 | 5 | 60 | 25 | 1089 | 660 | 693 | 400 | 420 |
| 11 | 8 | 12 | 18 | 12 | 20 | 2 | 16 | 4 | 400 | 240 | 240 | 144 | 144 |
| 12 | 16 | 17 | 26 | 16 | 33 | 7 | 112 | 49 | 1089 | 528 | 561 | 256 | 272 |
| ∑ | 98 | 186 | 235 | 162 | 284 | 49 | 442 | 245 | 7110 | 4012 | 4594 | 2284 | 2611 |
Коэффициенты уравнений найдем методом наименьший квадратов:

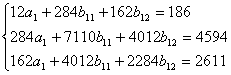
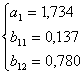 (решение системы найдено в программе MATLAB)
(решение системы найдено в программе MATLAB)
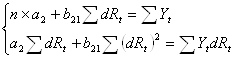
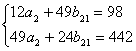
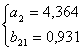
Таким образом, получена система структурных уравнений
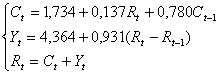
Задача 4
Динамика номинальной среднемесячной заработной платы одного работника области характеризуется следующими данными:
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Тыс. руб. | 3,2 | 3,1 | 3,5 | 3,5 | 3,7 | 4,0 | 4,1 | 4,0 | 4,1 | 4,2 | 4,3 | 5,4 |
Задание
1. Определите коэффициент автокорреляции первого порядка и дайте его интерпретацию.
2. Постройте линейное уравнение тренда. Дайте интерпретацию параметрам.
3. С помощью критерия Дарбина – Уотсона сделайте выводы относительно автокорреляции в остатках в рассматриваемом уравнении.
4. Дайте интервальный прогноз ожидаемого уровня номинальной заработной платы на январь следующего года.
Решение
1. Коэффициент автокорреляции первого порядка рассчитывается по следующей формуле:
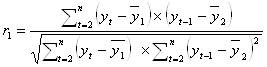
где 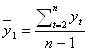 ;
; 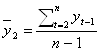
Для расчета коэффициента автокорреляции первого порядка составим расчетную таблицу:
Таблица 4.1 Расчетная таблица
| t | yt | yt-1 |
|
|
|
|
|
| 1 | 3,2 | - | - | - | - | - | - |
| 2 | 3,1 | 3,2 | -0,9 | 2,8 | -2,5 | 7,9 | 0,8 |
| 3 | 3,5 | 3,1 | -0,5 | 2,7 | -1,3 | 7,3 | 0,2 |
| 4 | 3,5 | 3,5 | -0,5 | 3,1 | -1,5 | 9,7 | 0,2 |
| 5 | 3,7 | 3,5 | -0,3 | 3,1 | -0,9 | 9,7 | 0,1 |
| 6 | 4,0 | 3,7 | 0,0 | 3,3 | 0,0 | 11,0 | 0,0 |
| 7 | 4,1 | 4,0 | 0,1 | 3,6 | 0,4 | 13,0 | 0,0 |
| 8 | 4,0 | 4,1 | 0,0 | 3,7 | 0,0 | 13,8 | 0,0 |
| 9 | 4,1 | 4,0 | 0,1 | 3,6 | 0,4 | 13,0 | 0,0 |
| 10 | 4,2 | 4,1 | 0,2 | 3,7 | 0,8 | 13,8 | 0,0 |
| 11 | 4,3 | 4,2 | 0,3 | 3,8 | 1,2 | 14,5 | 0,1 |
| 12 | 5,4 | 4,3 | 1,4 | 3,9 | 5,5 | 15,3 | 2,0 |
| Итого | 47,1 | 41,7 | 0,0 | 37,3 | 2,1 | 129 | 3,4 |
![]() = 3,991;
= 3,991;
![]() = 0,391.
= 0,391.
Коэффициент автокорреляции первого порядка равен:
![]() =
= ![]() = 0,1.
= 0,1.
Это значение (0,1) свидетельствует о слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней, т. е. слабой зависимости между номинальной среднемесячной заработной платы текущего и непосредственно предшествующего месяца.
2. Линейное уравнение трендов имеет вид:
![]()
Параметры a и b этой модели определяются обычным МНК. Система нормальных уравнений следующая:
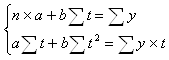
По исходным данным составит расчетную таблицу:
Таблица 4.2 Расчетная таблица
| t | y | yt | t2 | |
| 1 | 3,2 | 3,2 | 1 | |
| 2 | 3,1 | 6,2 | 4 | |
| 3 | 3,5 | 10,5 | 9 | |
| 4 | 3,5 | 14 | 16 | |
| 5 | 3,7 | 18,5 | 25 | |
| 6 | 4 | 24 | 36 | |
| 7 | 4,1 | 28,7 | 49 | |
| 8 | 4 | 32 | 64 | |
| 9 | 4,1 | 36,9 | 81 | |
| 10 | 4,2 | 42 | 100 | |
| 11 | 4,3 | 47,3 | 121 | |
| 12 | 5,4 | 64,8 | 144 | |
| Итого | 78 | 47,1 | 328,1 | 650 |
| Средние | 6,5 | 3,925 | 27,342 | 54,167 |
Система нормальных уравнений составит:
![]()
Используем следующие формулы для нахождения параметров:
![]() = 0,153;
= 0,153;
![]() = 2,927.
= 2,927.
Линейное уравнение трендов
![]() = 2,927 + 0,153* t
= 2,927 + 0,153* t
Параметр b = 0,153 означает, что с увеличение месяца на 1 месяц номинальная среднемесячная заработная плата увеличивается в среднем на 0,153 тыс. руб.
3. Для оценки существенности автокорреляции остатков используют критерий Дарбина – Уотсона:
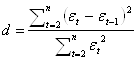
Коэффициент автокорреляции остатков первого порядка может определятся как:
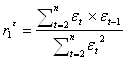
Для каждого момента (периода) времени t = 1 : n значение компонента ![]() определяется как
определяется как
![]()
Составим расчетную таблицу
Таблица 4.3 Расчетная таблица
| t | y |
|
|
|
|
|
|
|
| |
| 1 | 3,2 | 3,080 | 0,120 | - | - | - | 0,014 | - | - | |
| 2 | 3,1 | 3,233 | -0,133 | 0,120 | -0,253 | 0,064 | 0,018 | 0,018 | -0,016 | |
| 3 | 3,5 | 3,386 | 0,114 | -0,133 | 0,247 | 0,061 | 0,013 | 0,013 | -0,015 | |
| 4 | 3,5 | 3,539 | -0,039 | 0,114 | -0,153 | 0,023 | 0,002 | 0,002 | -0,004 | |
| 5 | 3,7 | 3,692 | 0,008 | -0,039 | 0,047 | 0,002 | 0,000 | 0,000 | 0,000 | |
| 6 | 4 | 3,845 | 0,155 | 0,008 | 0,147 | 0,022 | 0,024 | 0,024 | 0,001 | |
| 7 | 4,1 | 3,998 | 0,102 | 0,155 | -0,053 | 0,003 | 0,010 | 0,010 | 0,016 | |
| 8 | 4 | 4,151 | -0,151 | 0,102 | -0,253 | 0,064 | 0,023 | 0,023 | -0,015 | |
| 9 | 4,1 | 4,304 | -0,204 | -0,151 | -0,053 | 0,003 | 0,042 | 0,042 | 0,031 | |
| 10 | 4,2 | 4,457 | -0,257 | -0,204 | -0,053 | 0,003 | 0,066 | 0,066 | 0,052 | |
| 11 | 4,3 | 4,610 | -0,310 | -0,257 | -0,053 | 0,003 | 0,096 | 0,096 | 0,080 | |
| 12 | 5,4 | 4,763 | 0,637 | -0,310 | 0,947 | 0,897 | 0,406 | 0,406 | -0,197 | |
| Σ | 1,145 | 0,714 | 0,7 | -0,067 |
Критерий Дарбина – Уотсона равен ![]()
![]() = 1,604.
= 1,604.
Коэффициент автокорреляции равен ![]() = - 0,096.
= - 0,096.
Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При n = 12 месяцев и m = 1 (число факторов) нижнее значение d’ равно 0,97, а верхнее – 1,33. Фактическое значение d=1,604 > d’=1,33, следовательно, автокорреляция остатков отсутствует.
Чтобы проверить значимость отрицательного коэффициента автокорреляции, сравним фактическое значение d с (4-dL) и (4-dU):
| 4-dL | 4-dU | |
| 1,604 | 3,03 | 2,67 |
Из таблицы видно, что в обоих случаях фактическое значение меньше сравниваемых. Это означает отсутствие в остатках автокорреляции.
Так же принято считать, что если фактическое значение d близко к 2, то автокорреляции остатков нет. В нашем примере это совпадает.
4. В соответствии с интерпретацией параметров линейного тренда, каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста. Тогда:
а) Точечный прогноз составит:
Точечный прогноз по уравнению тренда – это расчетное значение переменной ![]() , полученное путем подстановки в уравнение тренда значений
, полученное путем подстановки в уравнение тренда значений
![]()
(n – длина динамического ряда, l – период упреждения).
![]() = 2,927 + 0,153* (12 + 1) = 4,916 (тыс. руб.)
= 2,927 + 0,153* (12 + 1) = 4,916 (тыс. руб.)
ожидаемый уровень номинальной заработной платы на январь следующего года.
б) Интервальный прогноз составит:
Доверительный интервал прогноза определяется с вероятностью 0,95, как:
![]()
![]() ;
;
где, tтабл=2,2281 - табличное значение t-критерия Стьюдента для уровня значимости α=0,05 и числа степеней свободы (n – 2 = 12 – 2 = 10); ![]() - стандартная ошибка точечного прогноза, которая рассчитывается по формуле:
- стандартная ошибка точечного прогноза, которая рассчитывается по формуле:
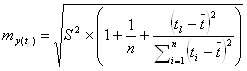
Данные необходимые для расчета представим в таблице.
Таблица 4.4 Расчетная таблица
| t | y |
|
|
|
|
|
|
|
| |
| 1 | 1 | 3,2 | 3,080 | 2 | -4,5 | 20,25 | 0,120 | 0,014 | -5,5 | 30,25 |
| 2 | 2 | 3,1 | 3,233 | 3 | -3,5 | 12,25 | -0,133 | 0,018 | -4,5 | 20,25 |
| 3 | 3 | 3,5 | 3,386 | 4 | -2,5 | 6,25 | 0,114 | 0,013 | -3,5 | 12,25 |
| 4 | 4 | 3,5 | 3,539 | 5 | -1,5 | 2,25 | -0,039 | 0,002 | -2,5 | 6,25 |
| 5 | 5 | 3,7 | 3,692 | 6 | -0,5 | 0,25 | 0,008 | 0,000 | -1,5 | 2,25 |
| 6 | 6 | 4 | 3,845 | 7 | 0,5 | 0,25 | 0,155 | 0,024 | -0,5 | 0,25 |
| 7 | 7 | 4,1 | 3,998 | 8 | 1,5 | 2,25 | 0,102 | 0,010 | 0,5 | 0,25 |
| 8 | 8 | 4 | 4,151 | 9 | 2,5 | 6,25 | -0,151 | 0,023 | 1,5 | 2,25 |
| 9 | 9 | 4,1 | 4,304 | 10 | 3,5 | 12,25 | -0,204 | 0,042 | 2,5 | 6,25 |
| 10 | 10 | 4,2 | 4,457 | 11 | 4,5 | 20,25 | -0,257 | 0,066 | 3,5 | 12,25 |
| 11 | 11 | 4,3 | 4,610 | 12 | 5,5 | 30,25 | -0,310 | 0,096 | 4,5 | 20,25 |
| 12 | 12 | 5,4 | 4,763 | 13 | 6,5 | 42,25 | 0,637 | 0,406 | 5,5 | 30,25 |
| Σ | 78 | 47,1 | 47,058 | 0,042 | 0,714 | 143 | ||||
| Сред | 6,5 |
![]() = 0,714 - остаточная сумма квадратов.
= 0,714 - остаточная сумма квадратов.
![]() = 0,267 – среднее квадратическое отклонение остаточной суммы квадратов
= 0,267 – среднее квадратическое отклонение остаточной суммы квадратов
![]()
 = 0,313
= 0,313
Таким образом, прогнозируемый уровень номинальной заработной платы на январь следующего года составит
![]()
![]() = 4,916 ± 2,2281*0,313 = 4,916 ± 0,697 тыс. руб.
= 4,916 ± 2,2281*0,313 = 4,916 ± 0,697 тыс. руб.
Выполненный прогноз уровня номинальной заработной платы на январь следующего года оказался надежным (р = 1 - ![]() = 0,95), и не точным, так как диапазон верхней и нижней границ доверительного интервала Dγ составляет 1,33 раза
= 0,95), и не точным, так как диапазон верхней и нижней границ доверительного интервала Dγ составляет 1,33 раза
Dγ = γ![]() mаx / γ
mаx / γ![]() min = 5,613 / 4,219 = 1,33.
min = 5,613 / 4,219 = 1,33.
Задача 5
Динамика численности незанятых граждан и объема платных услуг населению в регионе характеризуется следующими данными
| Месяц | Число незанятых граждан тыс.чел .,x1 | Объем платных услуг населению млрд.руб., y1 |
| Январь | 44,0 | 6,5 |
| Февраль | 45,5 | 7,0 |
| Март | 47,9 | 7,0 |
| Апрель | 48,3 | 7,4 |
| Май | 49,1 | 7,5 |
| Июнь | 49,9 | 7,2 |
| Июль | 50,5 | 7,5 |
| Август | 51,9 | 7,9 |
| Сентябрь | 52,3 | 8,2 |
| Октябрь | 52,3 | 8,5 |
| Ноябрь | 53,5 | 8,9 |
| Декабрь | 54,7 | 9,2 |
В результате аналитического выравнивания получены следующие уравнения трендов и коэффициент детерминации(t=1÷12):
А) для объема платных услуг населению
Ŷ1=6,3061+0,2196t ,R2=0,9259
Б) для численности незанятых граждан
̂х1=43,724+0,8937t , R2=0,989
Задание
Похожие работы
... активной части основных фондов в этом же периоде на 24,862 – 23,3 = 1,562 млн.грн по сравнению с двенадцатым периодом. Выводы и рекомендации Проведенный анализ технико-экономических показателей работы предприятия позволяет сделать вывод о том, что оно работает стабильно и постепенно развивается, хотя и невысокими темпами. Дальнейший рост фондоотдачи предприятия может быть обеспечен неск
... удобрений на 1 кг. Средняя ошибка аппроксимации = 1/25 ∙494,486 = 19,780% Ошибка аппроксимации 19,78 % > 12% – модель ненадежна и статистически незначима. Оценим тесноту связи с помощью показателей корреляции и детерминации. Тесноту связи показывает коэффициент корреляции: δx- показывает, что в среднем фактор Х меняется в пределах , 3,46 ± 4,672 δу - ...
... Hо. №29. ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. ИНТЕРПРИТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. Величину L, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один ил более моментов времени, — лаговыми переменными. Эконометрическое моделирование осуществляется с ...
... , характеризующих результаты экономической деятельности, структуру экономики и важнейшие взаимосвязи в национальном хозяйстве. Основным положением системы национальных счетов является расчет обобщающих показателей развития различных отраслей в рамках национальной экономики на различных стадиях воспроизводственных процессов, а также взаимоувязка этих показателей как между собой, так и во временных ...
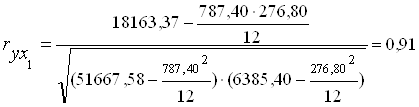


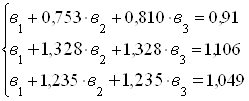
0 комментариев