Навигация
Дайте интерпретацию параметров уровней трендов
1. Дайте интерпретацию параметров уровней трендов.
2. Определите коэффициент корреляции между временными рядами, используя:
А) непосредственно исходные уровни
Б)о тклонения от основной тенденции
3). Сделайте вывод о тесноте связи между временными рядами.
4). Постройте вывод о тесноте связи между временными рядами. Дайте интерпретацию параметров уравнения.
Решение
Наиболее простую экономическую интерпретацию имеют параметры линейного тренда. Параметры линейного тренда можно интерпретировать так:
а – начальный уровень временного ряда в момент времени t = 0;
b – средний за период абсолютный прирост уровней ряда.
Для исходной задачи начальный уровень ряда для выпуска товаров соответствует значению 6,3061 млрд. руб., средний за период абсолютный прирост уровней ряда составляет 0,2196 млрд. руб. Параметр b > 0, значит уровни ряда равномерно возрастают на 0,2196 млрд. руб. каждый год.
Для числа незанятых граждан тыс,чел коэффициент а - начальный уровень ряда соответствует значению 43,724 тыс. чел.; абсолютное ускорение увеличения среднесписочной численности работников соответствует 0,8937.
Рассчитаем коэффициент корреляции между временными рядами, используя непосредственно исходные уровни. Коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Определяем его по формуле
rxy=![]()
Расчет параметров коэффициента корреляции
| № | X | Y | X² | x·y | y² | ŷ |
| |||||
| | ||||||||||||
| 1. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||
| 1. | 44 | 6,5 | 1936 | 286 | 42,25 | 15,96 | 78,9 | |||||
| 2. | 45,5 | 7 | 2070,25 | 318,5 | 49 | 16,2979 | 80,1 | |||||
| 3. | 46,8 | 7 | 2190,24 | 327,6 | 49 | 16,82494 | 82,08 | |||||
| 4. | 47,9 | 7,4 | 2294,41 | 354,46 | 54,76 | 17,08846 | 82,34 | |||||
| 5. | 48,8 | 7,5 | 2381,44 | 48,8 | 56,25 | 17,2644 | 82,98 | |||||
| 6. | 49,1 | 7,2 | 2410,81 | 353,52 | 51,84 | 17,25 | 83,62 | |||||
| 7. | 49,9 | 7,5 | 2490,01 | 374,25 | 56,25 | 17,3959 | 84,1 | |||||
| 8. | 50,5 | 7,9 | 2550,25 | 50,5 | 62,41 | 17,70334 | 85,22 | |||||
| 9. | 51,9 | 8,2 | 2693,61 | 425,58 | 67,24 | 17,79118 | 85,54 | |||||
| 10 | 52,3 | 8,5 | 2735,29 | 444,55 | 72,25 | 17,79118 | 85,85 | |||||
| 11 | 53,5 | 8,9 | 2862,25 | 476,15 | 79,21 | 18,0547 | 86,3 | |||||
| 12 | 54,7 | 9,2 | 2992,09 | 503,24 | 84,64 | 18,31822 | 87,46 | |||||
| ∑ | 594,9 | 92,8 | 29606,65 | 3963,15 | 725,1 | 207,7402 | 1011,49 | |||||
| ср.знач | 49,575 | 7,733333 | 2467,221 | 330,2625 | 60,425 | 17,31169 | 83,7075 |
sх = ![]() =
= ![]() = 3,08;
= 3,08;
sу = ![]() =
= ![]() =0,821.
=0,821.
rxy = ![]() = -20,7110 - связь слабая, прямая.
= -20,7110 - связь слабая, прямая.
При измерении корреляции между двумя временными рядами следует учитывать возможное существование ложной корреляции, что связано с наличием во временных рядах тенденции, т.е. зависимости обоих рядов от общего фактора времени. Для того чтобы устранить ложную корреляцию, следует коррелировать не сами уровни временных рядов, а их последовательные (первые или вторые) разности или отклонения от трендов (если последние не содержат тенденции).
Таким образом между временными рядами существует прямая слабая взаимосвязь.
Линейная регрессия сводится к нахождению уравнения вида
![]() = a + b*x
= a + b*x
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a и b.
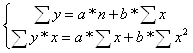 ,
,
Можно воспользоваться готовыми формулами, которые вытекают из этой системы
а = ![]() ;
;
b = ![]() =
=![]() = 0,008;
= 0,008;
а = 0,00286 – 0,701*0 = 7,334
Уравнение регрессии по отклонениям от трендов:
![]() = 7,334+ 0,008*х
= 7,334+ 0,008*х
Список используемой литературы
1. Практикум по эконометрике: Учеб. пособие / И. И. Елисеева, С. В. Курышева, Н. М. Гордеенко и др.; Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. – 192 с.
2. Эконометрика: Учебник / Под ред. И. И. Елисеевой. – М.: Финансы и статистика, 2001. – 344 с.
3. Мхитарян В.С., Архипова М.Ю. Эконометрика Московский международный институт эконометрики, информатики, финансов и права. - М., 2004. - 69 с.
4. Эконометрия - УП – Суслов – Ибрагимов – Талышева - Цыплаков - 2005 – 744 с.
Приложение №1
Таблица 1.2 Расчетная таблица
| y | x |
| ( |
|
| ( |
| ( |
| ( | |
| 1 | 35,8 | 9,4 | 5,240 | 27,458 | 41,559 | 10,999 | 120,978 | -5,759 | 33,166 | 3,930 | 15,445 |
| 2 | 22,5 | 2,5 | -8,060 | 64,964 | 22,248 | -8,312 | 69,089 | 0,252 | 0,064 | -2,970 | 8,821 |
| 3 | 28,3 | 3,9 | -2,260 | 5,108 | 26,166 | -4,394 | 19,307 | 2,134 | 4,554 | -1,570 | 2,465 |
| 4 | 26,0 | 4,3 | -4,560 | 20,794 | 27,285 | -3,275 | 10,726 | -1,285 | 1,651 | -1,170 | 1,369 |
| 5 | 18,4 | 2,1 | -12,160 | 147,866 | 21,128 | -9,432 | 88,963 | -2,728 | 7,442 | -3,370 | 11,357 |
| 6 | 31,8 | 6,0 | 1,240 | 1,538 | 32,043 | 1,483 | 2,199 | -0,243 | 0,059 | 0,530 | 0,281 |
| 7 | 30,5 | 6,3 | -0,060 | 0,004 | 32,883 | 2,323 | 5,396 | -2,383 | 5,679 | 0,830 | 0,689 |
| 8 | 29,5 | 5,2 | -1,060 | 1,124 | 29,804 | -0,756 | 0,572 | -0,304 | 0,092 | -0,270 | 0,073 |
| 9 | 41,5 | 6,8 | 10,940 | 119,684 | 34,282 | 3,722 | 13,853 | 7,218 | 52,100 | 1,330 | 1,769 |
| 10 | 41,3 | 8,2 | 10,740 | 115,348 | 38,201 | 7,641 | 58,385 | 3,099 | 9,604 | 2,730 | 7,453 |
| Σ | 305,6 | 54,7 | 0,000 | 503,884 | 305,600 | -0,001 | 389,468 | 0 | 114,411 | 0 | 49,722 |
| Сред. знач. | 30,56 | 5,47 | - | - | - | - | - | - | - | - | - |
Приложение 2.
Таблица значений F-критерия Фишера (двусторонний)
| d.f.2= n - k - 1) степени свободы остаточной дисперсии | степени свободы факторной дисперсии – d.f.1 = k | |||||||||||
| k=1 | k=2 | k=3 | k=4 | |||||||||
| Уровень значимости, α | ||||||||||||
| 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | 0,10 | 0,05 | 0,01 | |
| 1 | 39,9 | 161,5 | 4052 | 49,5 | 199,5 | 5000 | 53,6 | 215,72 | 5403 | 55,8 | 224,57 | 5625 |
| 2 | 8,5 | 18,5 | 98,5 | 9,0 | 19,0 | 99,00 | 9,2 | 19,16 | 99,2 | 19,2 | 19,25 | 99,30 |
| 3 | 5,54 | 10,13 | 34,1 | 5,46 | 9,6 | 30,82 | 5,39 | 9,28 | 29,5 | 5,34 | 9,12 | 28,71 |
| 4 | 4,54 | 7,71 | 21,2 | 4,32 | 6,9 | 18,00 | 4,19 | 6,59 | 16,7 | 4,11 | 6,39 | 15,98 |
| 5 | 4,06 | 6,61 | 16,3 | 3,78 | 5,79 | 13,27 | 3,62 | 5,41 | 12,1 | 3,52 | 5,19 | 11,39 |
| 6 | 3,78 | 5,99 | 13,8 | 3,46 | 5,14 | 10,92 | 3,29 | 4,76 | 9,8 | 3,18 | 4,53 | 9,15 |
| 7 | 3,59 | 5,59 | 12,3 | 3,26 | 4,74 | 9,55 | 3,07 | 4,35 | 8,5 | 2,96 | 4,12 | 7,85 |
| 8 | 3,46 | 5,32 | 11,3 | 3,11 | 4,46 | 8,65 | 2,92 | 4,07 | 7,6 | 2,81 | 3,84 | 7,01 |
| 9 | 3,36 | 5,12 | 10,6 | 3,01 | 4,26 | 8,02 | 2,81 | 3,86 | 7,0 | 2,69 | 3,63 | 6,42 |
| 10 | 3,29 | 4,96 | 10,0 | 2,92 | 4,10 | 7,56 | 2,73 | 3,71 | 6,6 | 2,61 | 3,48 | 5,99 |
| 11 | 3,23 | 4,84 | 9,7 | 2,86 | 3,98 | 7,20 | 2,66 | 3,59 | 6,2 | 2,54 | 3,36 | 5,67 |
| 12 | 3,18 | 4,75 | 9,3 | 2,81 | 3,88 | 6,93 | 2,61 | 3,49 | 6,0 | 2,48 | 3,26 | 5,41 |
| 13 | 3,14 | 4,67 | 9,1 | 2,76 | 3,80 | 6,70 | 2,56 | 3,41 | 5,7 | 2,43 | 3,18 | 5,20 |
| 14 | 3,10 | 4,60 | 8,9 | 2,73 | 3,74 | 6,51 | 2,52 | 3,34 | 5,6 | 2,39 | 3,11 | 5,03 |
| 15 | 3,07 | 4,54 | 8,7 | 2,70 | 3,68 | 6,36 | 2,49 | 3,29 | 5,4 | 2,36 | 3,06 | 4,89 |
| 16 | 3,05 | 4,49 | 8,5 | 2,67 | 3,63 | 6,23 | 2,46 | 3,24 | 5,3 | 2,33 | 3,01 | 4,77 |
| 17 | 3,03 | 4,45 | 8,4 | 2,64 | 3,59 | 6,11 | 2,44 | 3,20 | 5,2 | 2,31 | 2,96 | 4,67 |
| 18 | 3,01 | 4,41 | 8,3 | 2,62 | 3,55 | 6,01 | 2,42 | 3,16 | 5,1 | 2,29 | 2,93 | 4,58 |
| 19 | 2,99 | 4,38 | 8,2 | 2,61 | 3,52 | 5,93 | 2,40 | 3,13 | 5,0 | 2,27 | 2,90 | 4,50 |
| 20 | 2,97 | 4,35 | 7,9 | 2,59 | 3,49 | 5,72 | 2,38 | 3,10 | 4,9 | 2,25 | 2,87 | 4,31 |
| 21 | … | 4,32 | 8,0 | … | 3,47 | 5,78 | … | 3,07 | 4,9 | … | 2,84 | 4,37 |
| 22 | 2,95 | 4,30 | 7,9 | 2,56 | 3,44 | 5,72 | 2,35 | 3,05 | 4,8 | 2,22 | 2,82 | 4,31 |
| 23 | … | 4,28 | 7,9 | … | 3,42 | 5,66 | … | 3,03 | 4,8 | … | 2,80 | 4,26 |
| 24 | 2,93 | 4,26 | 7,8 | 2,54 | 3,40 | 5,61 | 2,33 | 3,01 | 4,7 | 2,19 | 2,78 | 4,22 |
| 25 | … | 4,24 | 7,8 | … | 3,38 | 5,57 | … | 2,99 | 4,7 | … | 2,76 | 4,18 |
| 26 | 2,91 | 4,22 | 7,7 | 25,2 | 3,37 | 5,53 | 2,31 | 2,98 | 4,6 | 2,17 | 2,73 | 4,14 |
| 30 | 2,88 | 4,17 | 7,56 | 2,49 | 3,32 | 5,39 | 2,28 | 2,92 | 4,5 | 2,14 | 2,69 | 4,02 |
| 40 | 2,84 | 4,08 | 7,31 | 2,44 | 3,23 | 5,18 | 2,23 | 2,84 | 4,3 | 2,09 | 2,61 | 3,83 |
| 60 | 2,79 | 4,00 | 7,08 | 2,39 | 3,15 | 4,98 | 2,18 | 2,76 | 4,1 | 2,04 | 2,53 | 3,65 |
| 80 | 2,77 | 8,96 | 6,96 | 2,37 | 3,11 | 4,88 | 2,16 | 2,72 | 4,0 | 2,02 | 2,48 | 3,56 |
| 100 | 2,76 | 3,94 | 6,90 | 2,36 | 3,09 | 4,82 | 2,14 | 2,70 | 3,98 | 2,00 | 2,46 | 3,51 |
| ∞ | 2,71 | 3,84 | 6,63 | 2,30 | 3,00 | 4,61 | 2,08 | 2,60 | 3,78 | 1,94 | 2,37 | 3,32 |
Шкала атрибутивных оценок тесноты корреляционной зависимости
| Значения показателей корреляции ( | Атрибутивная оценка тесноты выявленной зависимости | Значения показателей детерминации, % ( |
| До 0,3 | Слабая | До 10 |
| 0,3 – 0,5 | Умеренная | 10 – 25 |
| 0,5 – 0,7 | Заметная | 25 – 50 |
| 0,7 – 0,9 | Тесная | 50 – 80 |
| 0,9 и более | Весьма тесная | 80 и более |
Приложение 4
Случайная ошибка коэффициента асимметрии для выборок разного объема
| Объём выборки, |
|
|
| 4 | 1,014 | 0,926 |
| 5 | 0,913 | 0,866 |
| 6 | 0,845 | 0,816 |
| 7 | 0,794 | 0,775 |
| 8 | 0,752 | 0,739 |
| 9 | 0,717 | 0,707 |
| 10 | 0,687 | 0,679 |
| 11 | 0,661 | 0,655 |
| 12 | 0,637 | 0,632 |
| 13 | 0,616 | 0,612 |
| 14 | 0,597 | 0,594 |
| 15 | 0,580 | 0,577 |
| 16 | 0,564 | 0,562 |
| 17 | 0,550 | 0,548 |
| 18 | 0,536 | 0,535 |
| 19 | 0,524 | 0,522 |
| 20 | 0,512 | 0,511 |
| 21 | 0,501 | 0,500 |
| 22 | 0,491 | 0,490 |
| 23 | 0,481 | 0,480 |
| 24 | 0,472 | 0,471 |
| 25 | 0,464 | 0,463 |
Похожие работы
... активной части основных фондов в этом же периоде на 24,862 – 23,3 = 1,562 млн.грн по сравнению с двенадцатым периодом. Выводы и рекомендации Проведенный анализ технико-экономических показателей работы предприятия позволяет сделать вывод о том, что оно работает стабильно и постепенно развивается, хотя и невысокими темпами. Дальнейший рост фондоотдачи предприятия может быть обеспечен неск
... удобрений на 1 кг. Средняя ошибка аппроксимации = 1/25 ∙494,486 = 19,780% Ошибка аппроксимации 19,78 % > 12% – модель ненадежна и статистически незначима. Оценим тесноту связи с помощью показателей корреляции и детерминации. Тесноту связи показывает коэффициент корреляции: δx- показывает, что в среднем фактор Х меняется в пределах , 3,46 ± 4,672 δу - ...
... Hо. №29. ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. ИНТЕРПРИТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ. Величину L, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один ил более моментов времени, — лаговыми переменными. Эконометрическое моделирование осуществляется с ...
... , характеризующих результаты экономической деятельности, структуру экономики и важнейшие взаимосвязи в национальном хозяйстве. Основным положением системы национальных счетов является расчет обобщающих показателей развития различных отраслей в рамках национальной экономики на различных стадиях воспроизводственных процессов, а также взаимоувязка этих показателей как между собой, так и во временных ...
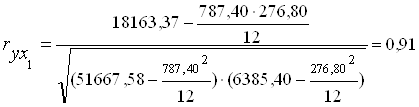


0 комментариев