Невизначене рівняння Ферма

2.2 Невизначене рівняння Ферма

Розглянемо тепер рівняння вигляду  (6).

Рівняння (6) називають невизначеним рівнянням Ферма, яке має велике значення у всій теорії діофантових рівнянь. Ми доведемо, що при кожному натуральному значенні 𝐷, відмінному від повного квадрата, це рівняння має нескінченно багато розв’язків в цілих числах, і знайдемо загальний метод знаходження всіх його розв’язків.

Теорема 6.

Нехай 𝐷 – ціле додатне, вільне від квадратів число і  () – розв'язок діофантового рівняння (6), тоді  є чисельником і знаменником відповідно одного із підхідних дробів до .

Доведення. Із  випливає, що  і

,

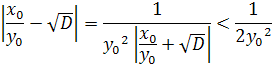
Тобто  – однин із підхідних дробів до . Оскільки  , що задовольняють рівняння (6) є взаємно простими числами, то із рівності

випливає: =.

Розклад  в ланцюговий дріб в загальному виглядає так:

 (7)

Виявляється, що розв’язками рівняння (6) можуть бути чисельники і знаменники тільки тих підхідних дробів  до  у яких індекс 𝑠 має вид .

Теорема 7.

Якщо () – розв'язок діофантового рівняння (6), то , де  - підхідний дріб до .

Доведення. В попередній теоремі було доведено, що якщо пара цілих додатних чисел є розв’язком рівняння (6), то =, де  - підхідний дріб до . Число  є коренем квадратного рівняння з цілими коефіцієнтами

. (8)

Повний частковий  розклад  в ланцюговий дріб є коренем деякого квадратного рівняння

з тим же дискримінантом, як у рівнянні (8) (при  ) маємо:

;

 - парне число, яке позначимо - 2. Розв’язуючи квадратне рівняння для  ,отримаємо  , тобто розклад  в ланцюговий дріб повинен мати той же період, як і в розкладі (7) числа і відрізняється від нього тільки на перший член розладу. Це може бути тільки при , ,  . Тепер залишається тільки вияснити, які саме з чисел  є розв’язками рівняння (6).

Теорема.

Нехай 𝐷 – ціле додатне, вільне від квадратів число, 𝑘 – довжина періоду розкладу  в ланцюговий дріб. Ми отримаємо всі розв’язки рівняння (6) в цілих додатних числах 𝑥 та 𝑦, якщо візьмемо:

де 𝑛 – довільне натуральне число, таке, що 𝑘𝑛 парне.

Доведення.

В попередній теоремі було встановлено, що всі цілі додатні розв’язки рівняння (6) знаходяться серед пар вигляду . Залишається тільки вияснити, при яких 𝑛 числа  задовольняють рівняння (6).

врозкладі  в ланцюговий дріб має вигляд:

,

тобто  (8).

Так, що підставляючи значення із формули (8), отримаємо:

 (9)

Оскільки  - ірраціональне, із рівності (9) випливає:

Помноживши першу з цих рівностей на , а другу на  і віднявши їх, отримаємо:

Пара ,  буде розв’язком рівняння (6) тоді і тільки тоді, коли , тобто при парних значеннях 𝑘𝑛. Найменшими додатними значеннями , які задовольняють рівняння Ферма (6) є:

, якщо 𝑘 парне.

, якщо 𝑘 непарне.

Приклад. 1) знайти найменші цілі додатні значення 𝑥, 𝑦, які задовольняють рівняння

Розкладаючи  в ланцюговий дріб, отримуємо:

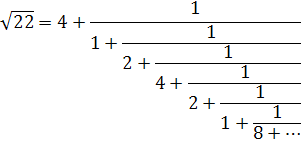
У даному прикладі 𝑘 = 6 – парне число, тому ,  - шукані значення 𝑥 та 𝑦. Обчислюючи , знаходимо , .

2) знайти найменші цілі, додатні значення 𝑥, 𝑦, які задовольняють рівняння

Розкладаючи в ланцюговий дріб  отримуємо:

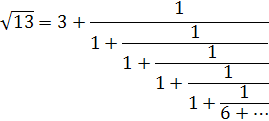
У цьому прикладі 𝑘=5, найменше парне 𝑘𝑛 дорівнює 10, тому шукані значення , . Обраховуючи, отримуємо , .

Аналогічно до рівняння (6) можна розв’язати рівняння

. (10)

Теореми доведені для рівняння (6) справедливі і для рівняння (10), але замість умови парності 𝑘𝑛 , треба поставити умову 𝑘𝑛 не ділиться на 2. Таким чином, при парних значеннях 𝑘 діофантове рівняння (10) не має розв’язків.