Теорема Лежандра

2.4 Теорема Лежандра

Розглянемо невизначене рівняння  (11). Вперше знайшов розв’язки рівняння (11) Лежандр, довівши наступну теорему:

Теорема 8.

Якщо 𝑎, 𝑏 і 𝑐 – попарно взаємно прості додатні цілі числа, вільні від квадратів, то невизначене рівняння

 

 

Має нетривіальні розв’язки в цілих числах 𝑥, 𝑦 і 𝑧, тоді і тільки тоді, коли мають розв’язки конгруенції

 

 (12)

 

Доведення.

Необхідність умов (12) очевидна. Доведемо їх достатність.

Нехай 𝑝 – довільний непарний простий дільник числа 𝑐. Тоді із (12) випливає, що конгруенція  маж нетривіальний розв'язок, наприклад, . В такому випадку форма  розкладається по модулю 𝑝 на лінійні множники:

 .

Такий же розклад правильний для форми , тобто має місце рівність

 , (13)

де  - цілочисельні лінійні форми. Аналогічні рівності мають місці і для непарних простих дільників 𝑝 коефіцієнтів 𝑎 і 𝑏, а також 𝑝 = 2, так, як

.

Знайдемо тепер такі лінійні форми , щоб виконувались рівності

Для всіх простих дільників 𝑝 коефіцієнтів 𝑎, 𝑏 і 𝑐. Тоді із рівності (13) отримаємо

 , (14)

Будемо надавати змінним  цілі значення, які задовольняють умови

 (15)

Якщо виключити із розгляду тривіальний випадок  (для нього твердження теореми очевидне), то із того, що числа 𝑎, 𝑏 і 𝑐 є взаємно простими, випливає що не всі числа , , будуть цілими. Значить, число наборів (𝑥, 𝑦, 𝑧), що задовольняють умови (15), строго більше, ніж  . Розглянемо значення, які приймає лінійна форма  при цих значеннях змінних. Так, як число наборів (𝑥, 𝑦, 𝑧) з умовою (15) більше числа лишків по модулю 𝑎𝑏𝑐, то для двох різних наборів (, , ) і (, , ) маємо

𝑙(, , )

Звідси, в силу лінійності форми , отримаємо, що при , ,  виконується конгруенція

𝑙(, , ).

 

Відповідно до (14),

 (16)

Оскільки для наборів (, , ) і (, , ) виконується (15), то

 ,

Значить,

Остання нерівність сумісна із конгруенцією (16) лише в тому випадку, коли

 

або коли

Перший випадок дає нетривіальний розв'язок, (, , ). У другому випадку існування нетривіального цілочисельного розв’язку рівняння (11) випливає із тотожності

Вище доведене дає ефективний алгоритм для знаходження нетривіального цілочисельного розв'язку рівняння (11).

 

 

Розділ ІІ. Приклади розв’язання діофантових рівнянь

 

§1. Приклади розв’язання лінійних діофантових рівнянь

Задача1. Розв’язати лінійне діофантове рівняння:

3𝑥.

Хоча одне рівняння з двома невідомими має нескінченне число розв’язків, неочевидно, що знайдеться хоча б одне з цілими додатними 𝑥 та 𝑦.

Знаючи, що 𝑥 та 𝑦 є цілими і додатними розв’яжемо це рівняння. Виділимо невідоме, коефіцієнт, якого менший, отримаємо:

,

звідки

.

Оскільки 𝑥, 6 і 𝑦 – цілі числа, то рівність може бути вірною лише за умови, що  є цілим числом. Позначимо його буквою 𝑡. Тоді

,

де

 ,

і значить,

Із останнього рівняння визначаємо 𝑦:

.

Оскільки 𝑦 та 𝑡 – цілі числа, то і  повинно бути деяким цілим числом . Тоді,

,

причому

звідки

+1.

Значення +1 підставимо в попередні рівності:

.

І так, для 𝑥 та 𝑦 ми знайшли представлення:

,

Взагалі кажучи, ми довели тільки те, що всякий цілочисельний розв'язок рівняння , має вигляд , , де  - деяке ціле число. Доведення того, що при довільному цілому  ми отримаємо деякий цілочисельний розв'язок даного рівняння, випливає, якщо провести аналогічні міркування в зворотному напрямку, підставивши знайдені значення 𝑥 та 𝑦 в початкове рівняння.

Оскільки , то і

,

З цих нерівностей знаходимо:

Цим самим величина  обмежується; вона більша за  (а значить і більша за ). Але оскільки - ціле і додатне число, то можна стверджувати, що для нього можливі лише наступні значення:

Тоді відповідні значення для 𝑥 та 𝑦 будуть такими:

,

Формули для  визначають розв’язки даного рівняння у цілих невідємниних числах.

 

Задача2. Розв’язати систему лінійних діофантових рівнянь:

 

 

Розв'язок:

Віднявши друге рівняння від першого, отримаємо одне рівняння з двома невідомими:

Знаходимо 𝑦:

Очевидно,  - ціле число. Позначимо його через 𝑡. Маємо:

Підставляємо вирази для 𝑦 та 𝑧 у друге із початкових рівнянь:

Отримаємо:

Так як  неважко встановити межі для 𝑡:

,

З цього можемо зробити висновок, що для 𝑡 можливі тільки два цілих значення: 𝑡=0, 𝑡=1.

Відповідні значення 𝑥, 𝑦 і 𝑧 будуть такими:

𝑡=0	0	1
𝑥=0	20	28
𝑦=0	20	0
𝑧=0	0	3

Перевірка

Задача3.

Вміння розв’язувати діофантові рівняння дає можливість виконати наступний математичний фокус.

Якщо помножити дату свого дня народження на 12, а номер місяця на 31 і знайти суму, то за такою сумою можна визначити дату народження.

Якщо, наприклад, задумана дата – 9 лютого, то наступні дії будуть такими:

За останнім числом 170 потрібно визначити задуману дату.

Задача зводиться до розв'язку рівняння з двома невідомими

у цілих, додатних числах, причому число місяця 𝑥 не більше 31, а номер місяця 𝑦 не більше 12.

Знаючи, що  і, знаходимо межі для

Отже , 𝑥=9, 𝑦=2.

Таким чином, дата народження 9-те число другого місяця, тобто 9 лютого.

 

Задача4.

Над двома цілими додатними числами були виконані наступні дії:

1.  Їх додали;

2.  Відняли від більшого менше;

3.  Перемножили;

4.  Поділили більше на менше.

Отримані результати додали і в результаті вийшло 243. Знайти ці числа.

Розв'язок.

Якщо більше число 𝑥, а менше число 𝑦, то

Якщо рівняння помножити на 𝑦, а потім розкрити дужки і звести подібні доданки, то отримаємо:

Але  Тому

Щоб 𝑥 було цілим числом, знаменник  повинен бути одним із дільників числа 243 (тому що 𝑦 не може мати спільні множники із 𝑦+1). Знаючи, що 243=, можна зробити висновок, що 243 ділиться тільки на наступні числа, які є точними квадратами: 1, , . І так, повинно дорівнювати 1,  або , звідки знаходимо 𝑦 (додатне), що дорівнює 8 або 2.

Тоді 𝑥 дорівнює

Тому шуканими числами будуть: 24 та 8 або 54 та 2.

Задача5.

Числа 46 та 96 мають цікаву властивість: їх добуток не міняється, якщо поміняти їх цифри місцями, тобто

Потрібно встановити, чи існують ще такі пари двозначних чисел з такою ж властивістю. Як знайти ці всі числа?

Розв'язок.

Позначимо цифри шуканих чисел через 𝑥 і 𝑦, 𝑧 і 𝑡, отримаємо рівняння:

Розкривши дужки та звівши подібні доданки отримуємо рівняння:

де 𝑥, 𝑦, 𝑧, 𝑡 – цілі числа, менші 10. Для того щоб знайти розв’язки складаємо із 9 цифр всі пари з рівними добутками:

Всіх рівностей 9. Із кожної можна скласти одну або дві пари шуканих чисел. Наприклад, із рівності  саємо один розв'язок:

Із рівності  знаходимо два розв’язки:

Аналогічно знаходимо наступні 14 розв’язків:

§2. Знаходження всіх цілих розв’язків діофантових рівнянь вищих порядків

 

Приклад 1.

Розв’язати в цілих числах рівняння

.

Розв'язок.

Розкладемо дане рівняння на множники таким чином:

 оскільки розв’язками даного рівняння можуть бути лише цілі числа, то числа  та  також мають бути цілими. З останньої рівності бачимо, що добуток цих чисел дорівнює 3, тому можливі випадки:

Отже, для знаходження всіх цілих розв’язків даного рівняння треба розв’язати наступні системи рівнянь, тобто розглянути всі можливі випадки , коли добуток чисел рівний трьом.

 

Відповідь: (0, 0), (1, ), (), ().

Приклад 2.

Розв’язати в цілих числах рівняння

 

.

 

Розв'язок.

Аналогічно до прикладу 1 розкладемо наше рівняння на множники і за таким же принципом розв’яжемо його.

Знаючи, що числа ,  цілі і в добутку дають , очевидно, що вони можуть набувати наступних значень:

Отже маємо такі системи рівнянь:

Відповідь:

 

 .

Приклад 3.

Розв’язати в цілих числах рівняння:

 

 

Розв'язок.

Перепишемо наше рівняння вигляді:

 

Тепер розв’яжемо дане рівняння, як квадратне відносно 𝑥:

Оскільки , маємо нерівність

Дискримінант набуватиме від’ємних значень при , тому 𝑦 належить проміжку. Враховуючи те, що 𝑦 є числом цілим, то він може набувати таких значень:

.

3наючи 𝑦, легко можемо знайти 𝑥:

при 𝑦=0,  ,

 .

при 𝑦=1,

0.

𝑥=0, 𝑥=2.

при 𝑦=2,  

 

 𝑥=1, 𝑥=2.

Відповідь: (0, 0), (0, 1), (1, 0), (1, 2), (2, 1), (2, 2).

 

Приклад 4.

Знайти всі розв’язки рівняння в цілих числах:

 

 

Розв'язок.

Нехай , де 𝑥, 𝑦, 𝑧 – цілі числа. Тоді число 𝑥 парне. Після заміни  отримаємо рівняння

Скоротимо на 2:

Очевидно, що 𝑦 парне число. Після заміни  отримаємо рівняння:

Знову скоротимо на 2:

З останнього рівняння бачимо, що 𝑧 парне число. Після заміни , отримаємо рівняння:

Отримали рівняння, яке має такий же вигляд як і початкове рівняння. Тому знову за таким же алгоритмом можемо довести, що  парні, і так далі. Але це можливо тільки в тому випадку, коли .

Отже, в цілих числах рівняння має єдиний розв'язок .

Приклад 5.

Знайти всі розв’язки рівняння в раціональних числах.

Розв'язок.

Очевидним є розв'язок , тому достатньо розглянути випадок, коли  (випадок  розглядується аналогічно).

Нехай , де – раціональне число. Тоді

тому 𝑘𝑦=, а значить  

Нехай  – нескоротний дріб. Тоді

 та .

Числа 𝑝 і 𝑝+𝑞 взаємно прості, тому число 𝑦 може бути раціональним тільки тому випадку, коли 𝑝= і 𝑝+𝑞= для деяких натуральних 𝑎 та 𝑏. Припустимо, що  Тоді

Приходимо, до суперечності, так, як між числами  та  не може знаходитись число . Тому 𝑞=1. Для будь-якого натурального 𝑝 числа

 та  раціональні і являються розв’язками рівняння . Ці числа будуть цілими лише при . В цьому випадку

Приклад 6.

Розв’язати в цілих числах рівняння

 

.

 

Розв'язок.

Перепишемо дане рівняння у вигляді :

Або

,

Звідки

Таким чином дане рівняння розпадається на два :

Або

(1)

(2)

Так як , то в (1) невідомий корінь 𝑥 може набувати цілі значення 0, 1, 4, 9, 16, а в (2) – лише цілі значення 0, 1, 4, 9. Відповідні їм значення 𝑦 такі: 64, 36, 16, 4, 0; 36, 16, 4, 0. Отже дане рівняння має 9 розв’язків в цілих числах.

Відповідь:

Приклад 7.

Розв’язати в цілих числах рівняння

 

 

Розв'язок.

Очевидно, що 𝑥 та 𝑧 не можуть бути від’ємними числами, так як при

а тому  має вигляд що можливо лише при парних значеннях 𝑦. Але з умови випливає, що 𝑦 не може бути парним числом, якщо .

Якщо , то рівняння має вигляд

звідки

Нехай  Маємо

Із цього рівняння випливає, що

 або , де 𝑡 – натуральне число.

Оскільки  і оскільки 𝑦 – непарне число, то 𝑧 – парне число або .

Нехай  Тоді , або , звідки

, . Тому або  тобто, звідки і тому

Якщо ж  , то 𝑥 довільне, 𝑎 𝑦. І так, при  ми маємо, крім тривіального розв'язку , де 𝛼 – будь яке натуральне число або нуль, лише ще один розв'язок:

При  . Очевидно, що непарних значеннях z дане рівняння не має розв’язків , при парних значеннях z рівняння зводиться до вигляду:

Отже, рівняння має тривіальний розв'язок  де 𝛼 – будь-яке натуральне число, і, крім того, ще має тільки три розв’язки:

 

Приклад 8.

Розв’язати в натуральних числах рівняння

 

Розв'язок.

Перепишемо дане рівняння у вигляді:

або

Оскільки дільниками числа 7 є лише числа  то шукані числа 𝑥 та 𝑦 треба шукати серед розв’язків наступних чотирьох систем:

Перша система має єдиний розв'язок в натуральних числах  третя система має також єдиний розв'язок в натуральних числах  Друга та четверта системи не мають розв’язків в натуральних числах.Отже, дане рівняння має рівно два розв’язки в натуральних числах: .

Приклад 9.

Розв’язати в цілих числах рівняння:

 

 

Розв'язок.

Ні одне із невідомих не може бути цілим від’ємним числом, так як рівності

неможливі при натуральних 𝑥, 𝑦, 𝑚, 𝑛.

Легко перевірити, що . Отже, 𝑥, 𝑦 – натуральні. Із умови випливає:

або

або

Число  – парне, якщо

Якщо , то , а тому із умови маємо

тобто,

Таким чином,  - розв'язок даного рівняння.

Якщо ж  повинно містити парну кількість доданків, а тому 𝑥 – парне число; нехай . Тоді

або ,

або .

Якщо 𝑧 – непарне число, то  - непарне число, що можливо лише при  тобто .

Тоді з умови маємо

тому  - другий розв'язок даного рівняння.

Якщо ж 𝑧 – парне число, тобто , то , а тому дане рівняння перепишемо у вигляді:

або ;

тому

останнє рівняння не має розв’язків, так як  ділиться на 5, а  не ділиться на 5.

Відповідь: (1, 1), (2, 3).

Приклад 10.

Розв’язати в натуральних числах рівняння:

 

 

Розв'язок.

Перепишемо рівняння у такому вигляді:

  (1)

Якщо  то , а тому , тобто ; відповідно, при  має місце нерівність

  (2)

Якщо , то , а тому ; значить, при  має місце нерівність

  (3)

Об’єднуючи нерівності (2) і(3), отримуємо, що при  ліва частина рівняння (1) додатна і тому відмінна від нуля.

Отже, при існуванні цілих додатних чисел даного рівняння 𝑥 має дорівнювати 1 або 2, а 𝑦 = 1. Підстановкою впевнюємось, що лише 𝑥 = 2, 𝑦 = 1 є розв’язком даного рівняння в натуральних числах.

Відповідь: (2, 1).

Приклад 11.

Розв’язати в цілих додатних числах систему рівнянь:

 

 

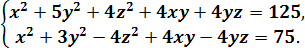
Розв'язок.

Додавши два рівняння системи, отримаємо

Звідки

(1)

Віднімаючи друге рівняння системи від першого, отримаємо

звідки

 (2)

Помноживши дві частини рівняння (2) на 2 і віднімаючи потім нове рівняння від (1), отримаємо

 (3)

Таким чином, із (2) та (3) випливає:

.

Оскільки , можливі лише два випадки:

а)

Відповідь: (4, 3, 1), (8, 1, 2).

Приклад 12.

 

Показати, що система рівнянь

 

має єдиний розв'язок

Розв'язок.

Так, як , то перше рівняння системи можна переписати у вигляді .

Оскільки (в означенням) , поділивши дві частини рівняння  на добуток , отримаємо рівносильне йому рівняння

Оскільки

є цілим числом, то і сума  повинна бути цілим числом. Останнє можливо лише в п’яти випадках:

Виконавши перевірку, впевнимося в тому, що тільки  задовольняє дану систему. Отже, система має єдиний розв'язок (1 ,1 ,2 ).

 

Висновок

 

У даній курсовій роботі розглядались діофантові рівняння. Таких рівнянь є надзвичайно багато, тому основною метою роботи було розглянути деякі з таких рівнянь та показати різні методи їх розв’язання.

Для окремих невизначених рівнянь існують відомі алгоритми знаходження всіх цілочисельних розв’язків, або алгоритми, що показують їх відсутність. Саме на такі рівняння акцентувалась увага у курсовій роботі.

При написанні курсової роботи я дізналась про різні методи знаходження розв’язків невизначених рівнянь. Розглянула цікаві діофантові рівняння для яких існують розв’язки в цілих числах, навчилась знаходити ці розв’язки, або показувати, що їх не існує.

Вміння розв’язувати діофантові рівняння дає змогу набагато простіше і швидше доводити існування чи не існування розв'язку деяких задач, а також при наявності розв’язків визначати їх кількість.

 

Література:

1.  Айєрленд К. А., Роузен М. Класическое введение в современную теорию чисел. – М.: Мир, 1987. – 416 с.

2.  Бухштаб А. А. Теорія чисел. – М.: Просвещение, 1996. – 284 с.

3.  Сивашинский И. Х. Теоремы и задачи по алгебре и элементарной математике. – М.: Гостехиздат, 1965. – 367 с.

4.  Перельман Я. И. Занимательная алгебра. – М.: Наука, 1967. - 200 с.

5.  Прасолов В. В. Многочлены. – М.: Наука, 2001. – 336 с.

6.  Шклярский Д .О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы алгебры и теории чисел (арифметика). – М.: Гостехиздат, 1950. – 382 с.

7.  Шнирельман Л. Г. Простые числа. – М.: Гостехиздат, 1940. – 178с.