Критерій відношення правдоподібності для великих вибірок

2. Критерій відношення правдоподібності для великих вибірок

Одним із найбільш універсальних методів побудови критеріїв перевірки складних гіпотез є метод відношення правдоподібності, суть якого полягає у наступному. Для перевірки гіпотези  проти альтернативи  вводиться статистика відношення правдоподібності

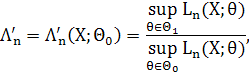
де , функція правдоподібності. Разом із статистикою  вводиться статистика

Будемо вважати, що виконуються умови регулярності, що забезпечують існування, єдність і асимптотичну нормальність оцінки максимальної правдоподібності  параметра . Розглянемо випадок простої гіпотези.

Теорема. Нехай потрібно перевірити просту гіпотезу фіксована внутрішня точка множини . Тоді для великих вибірок( ) при виконанні вказаних умов регулярності критерію відношення правдоподібності задається асимптотично критичною множиною

(1)

тобто при

де рівень значущості критерію.

Доведення. Покажемо, що з умов теореми слідує:

(2)

звідки випливає рівність (1). Якщо справедлива гіпотеза , то в силу спроможності оцінки максимальної правдоподібності при великих  точка близька до , тому для  можна записати розклад Тейлора відносно точки :

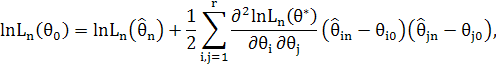
де Звідси випливає, що

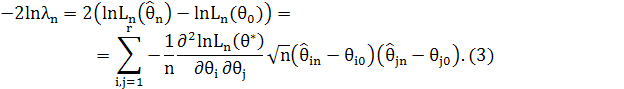
Оскільки слушна оцінка для , а другі похідні функції правдоподібності, за припущенням, неперервні по , то справедливо:

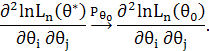
На основі закону великих чисел при  величина

збігається за ймовірністю( за розподілом ) до середнього значення

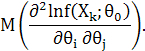
Таким чином, матриця граничних значень коефіцієнтів квадратичної форми у (3) співпадає з інформаційною матрицею . Звідси слідує, що випадковий вектор  має в границі такий же розподіл, як і нормальний  випадковий вектор  Таким чином, права частина (3) має в границі такий розподіл, як і квадратична форма . Тоді . Звідки і випливає співвідношення (2). Теорему доведено.

Розглянемо важливий приклад застосування викладених результатів до поліноміального розподілу

Приклад( метод відношення правдоподібності для поліноміального розподілу). Нехай проводяться незалежні випробування, в кожному з яких реалізується один із  можливих наслідків , тобто спостерігається випадкова величина , що приймає значення (, якщо наступила подія ). Позначимо через вектор ймовірностей цих подій( ) і через  вектор частот реалізацій відповідних наслідків в  випробуваннях( ). Як відомо, розподіл вектора  має поліноміальний розподіл . Припустимо тепер, що ймовірності подій  невідомі і потрібно перевірити гіпотезу  де заданий вектор, що задовольняє умовам: . Альтернативна гіпотеза має вигляд .

Тут роль параметра  відіграє вектор , але оскільки на значення параметрів накладена вимога , то бажано позбутись цього обмеження, виключивши, наприклад,. Таким чином, надалі покладаємо  і .

Оцінками максимальної правдоподібності для параметрів  є відносні частоти реалізацій відповідних подій, тобто , тому в даному випадку статистика відношення правдоподібності має вигляд:

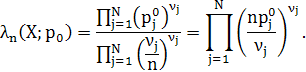
Звідси

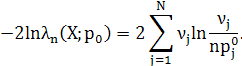
Якщо справедлива гіпотеза , то в границі при  ця статистика має розподіл , тому при заданому рівні значущості  критичну границю вибирають рівною . Тоді критична множина матиме вигляд: , причому критична точка  визначається із співвідношення:

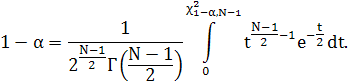
Тому, якщо

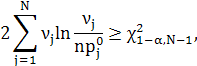
то гіпотеза  відхиляється( тобто вона не узгоджується із статистичними даними проведеного експерименту, і ймовірність того, що ми відхиляємо правильну гіпотезу не перевищує значення ), у протилежному випадку – приймається.

Приклад 2(метод відношення правдоподібності для перевірки значень параметрів нормального розподілу)

Розглядається вибірка з нормального розподілу. Потрібно перевірити гіпотезу про значення параметрів нормального розподілу за двосторонньої альтернативи. А саме, , альтернативна гіпотеза. Обчислимо статистику критерію. Для цього знайдемо функцію правдоподібності для нормального розподілу  . Тоді

.

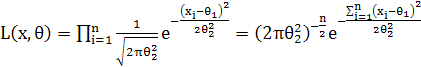Звідси,

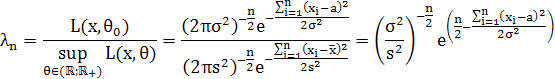
Тут,. Тому статистика критерію матиме вигляд:

.

У наступному розділі ми більш детально розглянемо застосування критерію відношення правдоподібності для великих вибірок до перевірки статистичних гіпотез.